贵州省毕节市织金县2023-2024学年八年级(下)期末数学试卷
试卷更新日期:2024-08-06 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 我国新能源汽车发展迅猛,下列新能源汽车标志既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 五边形的外角和等于( )
2. 五边形的外角和等于( )
A、180° B、360 ° C、540° D、720°3. 如图, , ,垂足为E , 若 ,则 的度数为( )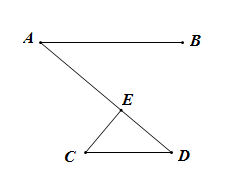 A、40° B、50° C、60° D、90°4. 用不等式表示:的倍与的差是正数( )A、 B、 C、 D、5. 如图,于点 , 于点 , 且 , 如果添上一个条件后,可以直接利用“”来证明≌ , 则这个条件应该是( )
A、40° B、50° C、60° D、90°4. 用不等式表示:的倍与的差是正数( )A、 B、 C、 D、5. 如图,于点 , 于点 , 且 , 如果添上一个条件后,可以直接利用“”来证明≌ , 则这个条件应该是( ) A、
A、
B、
C、
D、6. 把分解因式,结果是( )A、 B、 C、 D、7. 当时,分式的值为( )A、 B、 C、 D、分式无意义8. 函数的图象如图所示,当时,的取值范围是( ) A、 B、
A、 B、
C、 D、9. 如图,在中,将绕点顺时针旋转 , 和旋转后的对应点分别是和 , 连接 , 则的度数是( ) A、
A、
B、
C、
D、10. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( ) A、3 B、4 C、6 D、511. 计算的结果等于( )A、 B、 C、 D、12. 已知 , , 则代数式的值为( )A、 B、 C、 D、
A、3 B、4 C、6 D、511. 计算的结果等于( )A、 B、 C、 D、12. 已知 , , 则代数式的值为( )A、 B、 C、 D、二、填空题:本题共4小题,每小题4分,共16分。
-
13. 不等式的解集是 .14. 在平面直角坐标系中,点关于原点对称的点的坐标是 .15. 如图,在中, , , 现将沿着的方向平移到的位置,若平移的距离为 , 则图中的阴影部分的面积为 .
 16. 如图,中, , , 平分 , , 为的中点,则的长为 .
16. 如图,中, , , 平分 , , 为的中点,则的长为 .
三、解答题:本题共9小题,共98分。解答应写出文字说明,证明过程或演算步骤。
-
17.(1)、解不等式组:;(2)、因式分解: .18. 如图,在由边长为个单位长度的小正方形组成的网格中,的顶点均为格点网格线的交点 .
 (1)、以点为旋转中心,将旋转 , 得到 , 请画出;(2)、将线段向右平移个单位长度,再向上平移个单位长度,得到线段 , 画出线段点与点对应,点与点对应19. 已知:如图, , , 垂足分别为 , , , 与相交于点 .
(1)、以点为旋转中心,将旋转 , 得到 , 请画出;(2)、将线段向右平移个单位长度,再向上平移个单位长度,得到线段 , 画出线段点与点对应,点与点对应19. 已知:如图, , , 垂足分别为 , , , 与相交于点 . (1)、求证:;
(1)、求证:;
(2)、若 , , 求的长.20. 某学校八年级共甲、乙两个班,为丰富学生的体育活动购买了一批足球和篮球,足球和篮球的价格不同,如图是两个班级购买的足球和篮球的数量及消费的金额.
(1)、求每个足球和篮球的价格;(2)、若该校八年级在同一商店采购同种型号的足球和篮球共个,且他们的消费金额不超过元,该校八年级最多购买了多少个足球?21. 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB , F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE . 连接DE、DF、EF . (1)、求证:△ADF≌△CEF;(2)、试证明△DFE是等腰直角三角形.22. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)、求证:△ADF≌△CEF;(2)、试证明△DFE是等腰直角三角形.22. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上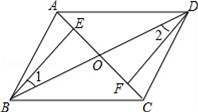 (1)、给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)、在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.23. 某学校决定购买一些杂志如果分别用元购买 , 两种杂志,则购买杂志的数量比杂志的数量多本,已知杂志的单价为杂志单价的 .
(1)、给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)、在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.23. 某学校决定购买一些杂志如果分别用元购买 , 两种杂志,则购买杂志的数量比杂志的数量多本,已知杂志的单价为杂志单价的 .
(1)、求 , 两种杂志的单价分别为多少元?(2)、学校计划购买 , 两种杂志共本,如果杂志本,总费用为元,请写出与的函数关系式;(3)、在的条件下学校计划购买杂志的数量不能超过本,那么应如何安排购买方案才能使费用最少,最少费用应为多少?24. (1)、求图中直线的函数表达式;(2)、如图 , 点在过点且平行于轴的直线上,过点作轴的垂线交直线于点 , 交直线于点 .
(1)、求图中直线的函数表达式;(2)、如图 , 点在过点且平行于轴的直线上,过点作轴的垂线交直线于点 , 交直线于点 .
当时,试用含的代数式表示与;
在的条件下,若 , 求的取值范围.25. 一发现探究
在中 , 点在平面内,连接并将线段绕点顺时针方向旋转与相等的角度,得到线段 , 连接 . (1)、【发现问题】如图 , 如果点是边上任意一点,则线段和线段的数量关系是;(2)、【探究猜想】如图 , 如果点为平面内任意一点前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由请仅以图所示的位置关系加以证明或说明;(3)、【拓展应用】如图 , 在中, , , , 是线段上的任意一点连接 , 将线段绕点顺时针方向旋转 , 得到线段 , 连接 , 请直接写出线段长度的最小值.
(1)、【发现问题】如图 , 如果点是边上任意一点,则线段和线段的数量关系是;(2)、【探究猜想】如图 , 如果点为平面内任意一点前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由请仅以图所示的位置关系加以证明或说明;(3)、【拓展应用】如图 , 在中, , , , 是线段上的任意一点连接 , 将线段绕点顺时针方向旋转 , 得到线段 , 连接 , 请直接写出线段长度的最小值.