【基础版】新北师大版数学七上 第四章 基本平面图形 章节测试卷
试卷更新日期:2024-08-03 类型:单元试卷
一、选择题(每题3分,共24分)
-
1. 如图所示,某同学的家在处,他想尽快赶到附近处搭顺风车.他选择第②条路线,用几何知识解释其道理正确的是( )
 A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线2. 如果A,B,C在同一条直线上,线段AB=6cm,BC=2cm,则A、C两点间的距离是( )A、8cm B、4cm C、8cm或4cm D、无法确定3. 如图,在内部作了一条射线,下列说法错误的是( )
A、两点确定一条直线 B、两点之间,线段最短 C、垂线段最短 D、经过一点有无数条直线2. 如果A,B,C在同一条直线上,线段AB=6cm,BC=2cm,则A、C两点间的距离是( )A、8cm B、4cm C、8cm或4cm D、无法确定3. 如图,在内部作了一条射线,下列说法错误的是( ) A、不可以用表示 B、这条射线记作射线 C、与是同一个角 D、4. ( )A、 B、 C、 D、5. 如图,能用、、三种方法表示同一个角的是A、
A、不可以用表示 B、这条射线记作射线 C、与是同一个角 D、4. ( )A、 B、 C、 D、5. 如图,能用、、三种方法表示同一个角的是A、 B、
B、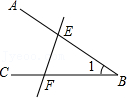 C、
C、 D、
D、 6. 若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论正确的是( )A、∠P=∠Q B、∠Q=∠R C、∠P=∠R D、∠P,∠Q,∠R互不相等7. 如图,正方形网格中每个小正方形的边长都为1,则∠α与∠β的大小关系为( )
6. 若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论正确的是( )A、∠P=∠Q B、∠Q=∠R C、∠P=∠R D、∠P,∠Q,∠R互不相等7. 如图,正方形网格中每个小正方形的边长都为1,则∠α与∠β的大小关系为( ) A、∠α<∠β B、∠α=∠β C、∠α>∠β D、无法估测8. 下列运算中正确的是( )A、31°12'36"=31.21° B、88°-57°23' 27"= 30°37' 33" C、15°48'36"+37°27'59"=52°16' 35" D、63.5°=63°50'
A、∠α<∠β B、∠α=∠β C、∠α>∠β D、无法估测8. 下列运算中正确的是( )A、31°12'36"=31.21° B、88°-57°23' 27"= 30°37' 33" C、15°48'36"+37°27'59"=52°16' 35" D、63.5°=63°50'二、填空题(每题3分,共15分)
-
9. 如图1,有 , 两个村庄在一条河(不计河的宽度)的两侧,现要建一座码头,使它到 , 两个村庄的距离之和最小,图2中所示的点即为所求码头的位置,其理由是 .
 10. 计算: .11. 过多边形的一个顶点的所有对角线把多边形分成个三角形,这个多边形的边数是 .12. 如图,点C , D在线段上,其中 , 若 , 则 .
10. 计算: .11. 过多边形的一个顶点的所有对角线把多边形分成个三角形,这个多边形的边数是 .12. 如图,点C , D在线段上,其中 , 若 , 则 . 13. 如图,射线OC平分∠AOB, , 则∠AOC的度数为 .
13. 如图,射线OC平分∠AOB, , 则∠AOC的度数为 .
三、作图题(共10分)
-
14. 如图,在同一平面内有一条线段和线段外一点D , 按要求完成下列作图:
 (1)、画直线和射线;(2)、在线段的延长线上取点C , 使(不写作法,保留作图痕迹);(3)、在(1)的条件下,比较线段的大小:(填“>”“<”或“=”),理由是 .
(1)、画直线和射线;(2)、在线段的延长线上取点C , 使(不写作法,保留作图痕迹);(3)、在(1)的条件下,比较线段的大小:(填“>”“<”或“=”),理由是 .四、解答题(共6题,给你个51分)
-
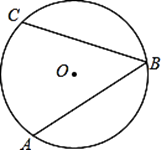
15. 计算:(1)、37°49'+44°28'.(2)、108°18'-56.5°.16. 如图,已知AB,CB为⊙O的两条弦,请写出图中所有的弧.
 17. 如图所示,在一条不完整的数轴(向右为正方向)上从左到右有点A、B、C,其中点A到点B的距离为3,点B到点C的距离为8,设点A、B、C所对应的数的和是m
17. 如图所示,在一条不完整的数轴(向右为正方向)上从左到右有点A、B、C,其中点A到点B的距离为3,点B到点C的距离为8,设点A、B、C所对应的数的和是m (1)、若以A为原点,则点B表示的数是 , 点C表示的数是 , m= .(2)、若以B为原点,则点A表示的数是 , 点C表示的数是 , m= .(3)、若原点O在图中数轴上,且点B到原点O的距离为4,则m= .18. 如图,AB=16cm,延长AB到C , 使BC=3AB , D是BC的中点,求AD的长度.
(1)、若以A为原点,则点B表示的数是 , 点C表示的数是 , m= .(2)、若以B为原点,则点A表示的数是 , 点C表示的数是 , m= .(3)、若原点O在图中数轴上,且点B到原点O的距离为4,则m= .18. 如图,AB=16cm,延长AB到C , 使BC=3AB , D是BC的中点,求AD的长度.
-

