湖北省黄石市黄石港区2023-2024学年七年级（下）期末数学试卷

试卷更新日期：2024-08-01 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 以下调查中，适合全面调查的是( )

A、了解全国中学生的视力情况 B、检测“神舟十六号”飞船的零部件
C、检测厦门的城市空气质量 D、调查某池塘中现有鱼的数量

查看试题解析
2. 在实数 $\sqrt{2}$ ， $\sqrt{25}$ ， $\frac{1}{2}$ ， $2024$ 中，属于无理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt{25}$ C、 $\frac{1}{2}$ D、2024

查看试题解析
3. 下列图形是我国几所大学的校徽，其中运用了“平移”制作的是（）

A、 B、 C、 D、

查看试题解析
4. 对不等式 $\frac{x - 1}{2} - \frac{x + 3}{8} > 1$ ，给出了以下解答：
①去分母，得 $4 (x - 1) - (x + 3) > 8$ ；②去括号，得 $4 x - 4 - x + 3 > 8$ ；③移项、合并同类项，得 $3 x > 9$ ；④两边都除以3，得 $x > 3$ 其中错误开始的一步是（）

A、① B、② C、③ D、④

查看试题解析
5. “凌波仙子生尘袜，水上轻盈步微月．”宋朝诗人黄庭坚以水中仙女借喻水仙花．如图，将水仙花图置于正方形网格中，点A，B，C均在格点上．若点 $A (- 2, 3)$ ， $B (0, 1)$ ，则点C的坐标为（）

A、 $(4, 2)$ B、 $(2, 2)$ C、 $(1, 2)$ D、 $(2, 1)$

查看试题解析
6. 下列图形中，由 $∠ 1 = ∠ 2$ 能得到 $A B / / C D$ 的图形有( )

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
7. 如图是由截面为同一种长方形的墙砖粘贴的部分墙面，其中三块横放的墙砖比一块竖放的墙砖高 $10 c m$ ，两块横放的墙砖比两块竖放的墙砖低 $40 c m$ ，则每块墙砖的截面面积是（）

A、 $600 c m^{2}$ B、 $1200 c m^{2}$ C、 $525 c m^{2}$ D、 $300 c m^{2}$

查看试题解析
8. 如图，线段 $A B$ 经过平移得到线段 $A^{'} B^{'}$ ，其中点 $A$ ， $B$ 的对应点分别为点 $A^{'}$ ， $B^{'}$ ，这四个点都在格点上．若线段 $A B$ 上有一个点 $P (a, b)$ ，则点 $P$ 在 $A^{'} B^{'}$ 上的对应点 $P^{'}$ 的坐标为( )

A、 $(a - 2, b + 3)$ B、 $(a - 2, b - 3)$ C、 $(a + 2, b + 3)$ D、 $(a + 2, b - 3)$

查看试题解析
9. 如图，在 $△ A B C$ 中， $B E$ ， $C E$ ， $C D$ 分别平分 $∠ A B C$ ， $∠ A C B$ ， $∠ A C F$ ， $A B / / C D$ ，下列结论： $① ∠ A = ∠ A B C$ ； $② ∠ B E C = 90 ° + ∠ A B D$ ； $③ ∠ A = ∠ D$ ； $④ 2 ∠ B E C - ∠ A = 180 °$ ，其中所有正确结论的序号是( )

A、 $① ②$ B、 $③ ④$ C、 $① ② ④$ D、 $① ② ③ ④$

查看试题解析
10. 已知关于 $x$ ， $y$ 的方程组 $① \{\begin{array}{l} 4 x + 3 y = 16, \\ b x + a y = 28 \end{array}$ 的解 $x$ ， $y$ 比 $② \{\begin{array}{l} 3 x + 2 y = 16, \\ a x - b y = - 8 \end{array}$ 相应的解 $x$ ， $y$ 正好都小 $1 .$ 则 $a$ ， $b$ 的值分别为( )

A、 $2$ 和 $3$ B、 $- 2$ 和 $- 3$ C、 $6$ 和 $4$ D、 $- 6$ 和 $- 4$

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分。

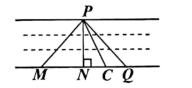
11. 如图所示，要在河堤两岸搭建一座桥，搭建方式中最短的是线段 $P N$ ，理由是．

查看试题解析
12. 已知：若 $\sqrt{3.65}$ ≈1.910， $\sqrt{36.5}$ ≈6.042，则 $\sqrt{365000}$ ≈ ．

查看试题解析
13. 在平面直角坐标系中，已知点 $A (3, - 2)$ ， $B (- 5,0)$ ， $O$ 为坐标原点，则三角形 $A O B$ 的面积为．

查看试题解析
14. 母亲节那天，很多同学给妈妈准备了鲜花和礼盒．从图中信息可知一束鲜花的价格是元．

查看试题解析
15. 高斯函数 $[x]$ ，也称取整函数，即 $[x]$ 表示不超过 $x$ 的最大整数，例如： $[2.5] = 2$ ， $[5] = 5$ ， $[- 2.5] = - 3 .$ 若关于 $x$ 的不等式组 $\{\begin{array}{l} \frac{2 x - 4}{3} \leq x - 1 \\ [a] - x > 0 \end{array}$ 的整数解恰有 $3$ 个，则 $a$ 的取值范围为．

查看试题解析

三、计算题：本大题共3小题，共22分。

16. 计算 $\sqrt[3]{- 8} + | 2 - \sqrt{5} | + \sqrt{{(- 3)}^{2}} - (- \sqrt{5})$ ．

查看试题解析
17. 计算

(1)、解方程组 $\{\begin{array}{l} x - y = 6 \\ 2 x + y = 18 \end{array}$ ．

(2)、解不等式组 $\{\begin{array}{l} 5 x - 1 > 3 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ ，并把不等式组的解集在数轴上表示．

查看试题解析
18. 若平面直角坐标系上点 $P (x, y)$ 的横、纵坐标满足关于 $x$ ， $y$ 的方程组，则称点 $P$ 为该方程组的关联点，如点 $N (2,1)$ 为方程组 $\{\begin{array}{l} 2 x - y = 3 \\ x + y = 3 \end{array}$ 的关联点．

(1)、若点 $E (1,2)$ 为关于 $x$ ， $y$ 的方程组 $\{\begin{array}{l} 7 x - 2 y = a \\ 2 x - b y = 2 \end{array}$ 的关联点，则 $a =$ ， $b =$ ；、

(2)、已知点 $A (x, y)$ 为关于 $x$ ， $y$ 的方程组 $\{\begin{array}{l} 7 x + 2 y = 1 \\ 2 x - y = 3 m - 2 \end{array}$ 的关联点，点 $B (x, y)$ 为关于 $x$ ， $y$ 的方程组 $\{\begin{array}{l} 2 x + y = - n + 3 \\ x - 2 y = 7 \end{array}$ 的关联点；若点 $A$ 与点 $B$ 重合，求点 $A$ 的坐标，并求出 $m$ ， $n$ 的值；

(3)、已知 $P (x, y)$ 为关于 $x$ ， $y$ 的方程组 $\{\begin{array}{l} x + 2 y = 3 m - 2 n - 5 \\ 2 x - y = m + n - 10 \end{array}$ 的关联点，若点 $P$ 在第二象限，且符合条件的所有整数 $m$ 之和为 $9$ ，求 $n$ 的范围．

查看试题解析

四、解答题：本题共6小题，共53分。解答应写出文字说明，证明过程或演算步骤。

19. 如图，从 $① ∠ 1 = ∠ 2 ② ∠ C = ∠ D ③ ∠ A = ∠ F$ 三个条件中选出两个作为已知条件，另一个作为结论可以组成 $3$ 个命题．

(1)、这三个命题中，真命题的个数为；

(2)、选择一个真命题，并且证明， $($ 要求写出每一步的依据 $)$
如图，已知_▲_，
求证：_▲_
证明：_▲_

查看试题解析
20. 如图，把 $△ A B C$ 向上平移 $3$ 个单位，再向右平移 $3$ 个单位得到 $△ A^{'} B^{'} C^{'}$ ．

(1)、在图中画出 $△ A^{'} B^{'} C^{'}$ ；

(2)、请写出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(3)、求出 $△ A B C$ 的面积．

查看试题解析
21. 某学校为了调研学生地理生物的真实水平．随机抽查了部分学生进模拟测试 $($ 地理 $50$ 分，生物 $50$ 分，满分 $100$ 分 $)$ ．
【收集数据】 $85$ ， $95$ ， $88$ ， $68$ ， $88$ ， $86$ ， $95$ ， $93$ ， $87$ ， $93$ ， $98$ ， $99$ ， $88$ ， $100$ ， $97$ ， $80$ ， $85$ ， $92$ ， $94$ ， $84$ ， $80$ ， $78$ ， $90$ ， $98$ ， $85$ ， $96$ ， $98$ ， $86$ ， $93$ ， $80$ ， $86$ ， $100$ ， $82$ ， $78$ ， $98$ ， $88$ ， $100$ ， $76$ ， $88$ ， $99 ($ 单位：分 $)$
【整理数据】
成绩 $($ 单位：分 $)$
$60 \leq x < 70$
$70 \leq x < 80$
$80 \leq x < 90$
$90 \leq x \leq 100$
频数 $($ 人数 $)$
$1$
$m$
$n$
$19$
【分析数据】

(1)、本次抽查的样本容量是；

(2)、填空： $m =$ _▲_， $n =$ _▲_，补充完整频数分布直方图；

(3)、若分数在 $90 \leq x \leq 100$ 的为优秀，估计全校七年级 $800$ 名学生中优秀的人数．

查看试题解析

22. 根据如表素材，完成表中的两个任务．

背景	在中国传统节日“端午节”期间，某爱心企业准备购买粽子慰问敬老院老人．
素材 $1$	某商场开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打九折，乙品牌粽子打八折．
素材 $2$	已知打折前，买 $5$ 盒甲品牌粽子和 $5$ 盒乙品牌粽子共需 $900$ 元；打折后，买 $6$ 盒甲品牌粽子和 $4$ 盒乙品牌粽子共需 $796$ 元．

(1)、【任务一：确定单价】打折前，甲、乙两种品牌粽子每盒分别为多少元？

(2)、【任务二：拟定方案】在商场促销期间，某爱心企业准备为敬老院购买甲、乙两种品牌粽子共

50

盒，总费用不超过

3500

元，问最多可购买多少盒甲品牌粽子？

查看试题解析

23. 在综合与实践课上，班级开展了以两条平行线和直角三角尺为主题的数学活动．

(1)、【初步感知】如图 $1$ ，若三角尺的 $60 °$ 角的顶点 $G$ 放在 $C D$ 上，若 $∠ 2 = 70 °$ ，则 $∠ 1$ 的度数为；

(2)、【自主探究】将一副三角板如图 $2$ 所示摆放，直线 $G H / / M N .$ 若三角板 $A B C$ 不动，而三角板 $D E F$ 绕点 $D$ 以每秒 $3 °$ 的速度顺时针旋转，设旋转时间为 $t$ 秒 $(0 < t < 120)$ ，求当旋转到 $D F / / B C$ 时， $t$ 的值是多少？

(3)、【探究拓展】现将三角板 $A B C$ 绕点 $A$ 以每秒 $1 °$ 的速度顺时针旋转，同时三角板 $D E F$ 绕点 $D$ 以每秒 $3 °$ 的速度顺时针旋转，如图 $3$ ，设时间为 $t$ 秒，当 $0 \leq t \leq 120$ 时，若边 $B C$ 与三角板 $D E F$ 的一条直角边 $($ 边 $D E$ ， $D F)$ 平行，求出所有满足条件的 $t$ 值 $. ($ 请直接写出满足条件的 $t$ 值 $)$

查看试题解析
24. 如图 $1$ ，在平面直角坐标系中，点 $A (- 2,0)$ ， $B (0,4)$ ，动点 $C (m, m)$ 在直线 $L$ 上运动 $($ 直线 $L$ 上所有点的横坐标与纵坐标相等 $)$ ．

(1)、如图 $2$ ，当点 $C$ 在第一象限时，依次连接 $A$ 、 $B$ 、 $C$ 三点， $A C$ 交 $y$ 轴于点 $D$ ，连接 $O C$ ，
$①$ 试求出 $S_{△ A O C} ($ 用含 $m$ 的式子表示 $)$ ；
$②$ 当 $S_{△ A B C} = 5$ ，求出点 $C$ 的坐标．

(2)、如图 $3$ ，当点 $C$ 与 $A$ 、 $B$ 两点在同一条直线上时，求出 $C$ 点的坐标；

(3)、当 $10 \leq S_{△ B O C} \leq 20$ ，求 $m$ 的取值范围．

查看试题解析

成绩 $($ 单位：分 $)$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
频数 $($ 人数 $)$	$1$	$m$	$n$	$19$