贵州省毕节市金沙县2023-2024学年七年级下学期期末数学试题

试卷更新日期：2024-08-01 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共36分．每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置填涂）

1. “十二生肖”是中国文化的代表之一，被联合国教科文组织列为人类非物质文化遗产，某同学在新年来临之际，通过简笔画描绘其一家四人的生肖属相，分别代表“龙”“猪”“猴”“鸡”，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 目前全球最薄的手撕钢产自中国，厚度只有0.015毫米，约是A4纸厚度的六分之一，已知1毫米 $= 1$ 百万纳米，0.015毫米等于多少纳米？将结果用科学记数法表示为（）

A、 $0.15 \times 1 0^{3}$ 纳米 B、 $1.5 \times 1 0^{4}$ 纳米 C、 $15 \times 1 0^{- 5}$ 纳米 D、 $1.5 \times 1 0^{- 6}$ 纳米

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- 2 m^{2})}^{3} = - 8 m^{6}$ C、 $(x + y)^{2} = x^{2} + y^{2}$ D、 $2 a b + 3 a^{2} b = 5 a^{3} b^{2}$

查看试题解析
4. 下列式子中，不能用平方差公式运算的是（）

A、 $(2 - a) (- a - 2)$ B、 $(3 x + 2 y) (2 y - 3 x)$ C、 $(4 m - 2 n) (4 m + 2 n)$ D、 $(x - 3) (3 - x)$

查看试题解析
5. 如图， $A B ∥ C D$ ，若 $∠ D = 5 0^{∘}$ ，则 $∠ 1$ 的度数为（）

A、 $15 0^{∘}$ B、 $14 0^{∘}$ C、 $13 0^{∘}$ D、 $12 0^{∘}$

查看试题解析
6. 下列事件是必然事件的是（）

A、打开电视机，CCTV1正在播放“嫦娥六号完成人类首次月背采样”的新闻 B、从两个班级中任选三名学生担任学校安全督查员，至少有两名学生来自同一个班级 C、小明在销售平台一定能抢到龙舟节开幕式门票 D、从《西游记》《红楼梦》《三国演义》《水浒传》这四本书中随机选取一本是《三国演义》

查看试题解析
7. 小亮在放学回家的路上，看到同学小明在前方，便加快速度追赶小明，在距离学校60米处追上了小明，如图反映了这一过程，其中 $s$ （单位：米）表示与学校的距离， $t$ （单位：秒）表示时间．根据相关信息，以下说法错误的是（）

A、开始时小明与小亮之间的距离是20米 B、15秒时小亮追上了小明 C、小亮走了40米追上小明 D、小亮追上小明时，小明走了40米

查看试题解析
8. 一副直角三角板按如图所示的方式摆放，点 $E$ 在 $A B$ 的延长线上，当 $D F ∥ A B$ 时， $∠ E D B$ 的度数为（）

A、 $1 0^{∘}$ B、 $1 5^{∘}$ C、 $3 0^{∘}$ D、 $4 5^{∘}$

查看试题解析
9. 如图， $y$ 与 $x$ 的关系式为（　　）

A、 $y = x + 55$ B、 $y = x - 35$ C、 $y = 125 - x$ D、 $y = x + 35$

查看试题解析
10. 如图所示，已知AE=AC，∠C=∠E，下列条件中，无法判定△ABC≌△ADE的是( )

A、∠B=∠D B、BC=DE C、∠1=∠2 D、AB=AD

查看试题解析
11. 如图，要测量池塘两岸相对的两点 $A$ ， $B$ 的距离，小明在池塘外取 $A B$ 的垂线 $B F$ 上的点 $C$ ， $D$ ，使 $B C = C D$ ，再画出 $B F$ 的垂线 $D E$ ，使 $E$ 与 $A$ ， $C$ 在一条直线上，这时测得 $D E$ 的长就是 $A B$ 的长，依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $H L$

查看试题解析
12. 均匀地向一个容器注水，最后将容器注满．在注水过程中，水的高度 $h$ 随时间 $t$ 的变化规律如图所示，则这个容器的形状可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每小题4分，共16分）

13. 计算： ${(4 x^{2})}^{3} =$ ．

查看试题解析
14. 如图，飞镖游戏板由含大小相等的等腰直角三角形格子构成，小东向游戏板随机投掷一枚飞镖，击中黑色区域的概率是．

查看试题解析
15. 如图， $A B ∥ C F$ ， $E$ 为 $D F$ 的中点，若 $A B = 7 c m$ ， $C F = 5 c m$ ，则 $B D =$ $c m$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A D$ 是 $∠ B A C$ 的平分线， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ， $D E = 2$ ， $A C = 4$ ，则 $△ A D C$ 的面积为．

查看试题解析

三、解答题（本大题共9题，共98分，解答应写出必要的文宇说明、证明过程或演算步骤）

17. 计算：

(1)、 $- 1^{2024} + | - 3 | + (π - 2024)^{0} - {(- \frac{1}{2})}^{- 3}$ ；

(2)、 $[{(2 x^{2})}^{3} - 6 x^{3} (x^{3} - 2 x^{2})] \div 2 x^{2}$ ．

查看试题解析
18. 先化简，再求值： $(2 a - 1)^{2} + 6 a (a + 1) - (3 a + 2) (3 a - 2)$ ，其中 $a^{2} + 2 a - 2024 = 0$ ．

查看试题解析
19. 如图，已知在 $△ A B C$ 中，点 $D$ 在边 $A C$ 上，且 $A B = A D$ ．

(1)、用尺规作图法，作 $∠ B A C$ 的平分线 $A P$ ，交 $B C$ 于点 $P$ ； $($ 保留作图痕迹，不要求写作法 $)$

(2)、在 $(1)$ 的条件下，连接 $P D$ 、求证： $P D = P B$ ．

查看试题解析
20. 如图所示，在长度为1个单位长度的小正方形组成的正方形网格中， $△ A B C$ 的三个顶点 $A$ ， $B$ ， $C$ 都在格点上．

(1)、在图中画出与 $△ A B C$ 关于直线 $y$ 成轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、求 $△ A B C$ 的面积；

(3)、在直线 $x$ 上找出一点 $P$ ，使得 $P B + P C$ 的值最小（不需要计算，在图上直接标记出点 $P$ 的位置）．

查看试题解析
21. 对某篮球运动员进行3分球投篮测试结果如表所示：
投篮次数 $n$
10
50
100
150
200
命中次数 $m$
4
25
65
90
120
命中率
0.4

(1)、计算表中投篮50次、100次、150次、200次相应的命中率；

(2)、这个运动员3分球投篮命中的概率约是多少？、

(3)、估计这个运动员3分球投篮30次能得多少分．

查看试题解析
22. 地表以下岩层的温度 $/^{∘} C$ 与所处深度 $/ k m$ 有如下关系：
深度 $/ k m$
1
2
3
4
5
温度 $/^{∘} C$
55
90
125
160
195

(1)、上表中自变量 $x$ 是，因变量 $y$ 是；

(2)、请写出 $y$ 与 $x$ 的关系式；

(3)、根据（2）中的关系式，估计地表以下7 $k m$ 处岩层的温度．

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：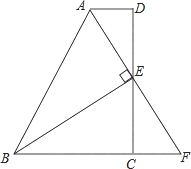

(1)、FC=AD；

(2)、AB=BC+AD．

查看试题解析
24. 乘法公式的探究及应用：
数学活动课上，老师准备了若干个如图1的三种纸片：A种纸片是边长为 $a$ 的正方形，B种纸片是边长为 $b$ 的正方形，C种纸片是长为 $b$ 、宽为 $a$ 的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．

(1)、请用两种不同的方法表示图2大正方形的面积：
方法1：，方法2：；

(2)、观察图2，请你写出三个代数式 $(a + b)^{2}$ ， $a^{2} + b^{2}$ ， $a b$ 之间的数量关系：；

(3)、根据（2）中的等量关系，解决如下问题：
①已知 $a + b = 7$ ， $a^{2} + b^{2} = 33$ ，求 $a b$ 的值；
②已知 $(2024 - a)^{2} + (a - 2022)^{2} = 8$ ，求 $(2024 - a) (a - 2022)$ 的值．

查看试题解析
25. 综合与探究
一张直角三角形纸片 $A B C$ ， $∠ B A C = 9 0^{∘}$ ，其中 $∠ A C B = ∠ A B C = 4 5^{∘}$ ， $D$ ， $E$ 分别是 $B C$ ， $A C$ 边上一点．将 $△ C D E$ 沿 $D E$ 折叠，点 $C$ 的对应点为点 $C^{'}$ ．

(1)、【特例感知】如图1，若 $C^{'} D ∥ A B$ ，则 $∠ 1 =$ $^{∘}$ ， $∠ 2 =$ $^{∘}$ ；

(2)、【问题探究】如图2，若点 $C^{'}$ 落在直角三角形纸片 $A B C$ 上，请探究 $∠ 1$ 与 $∠ 2$ 的数量关系，并说明理由；

(3)、【拓展延伸】如图3，若点 $C^{'}$ 落在直角三角形纸片 $A B C$ 外，（2）中 $∠ 1$ 与 $∠ 2$ 的数量关系还成立吗？若成立，请说明理由；若不成立，请求出 $∠ 1$ 与 $∠ 2$ 的数量关系．

查看试题解析

投篮次数 $n$	10	50	100	150	200
命中次数 $m$	4	25	65	90	120
命中率	0.4

深度 $/ k m$	1	2	3	4	5
温度 $/^{∘} C$	55	90	125	160	195