湖北省荆州市监利市2023-2024学年八年级（下）期末数学试卷

试卷更新日期：2024-08-01 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 在数 $- \sqrt{3} 、 2 、 0 、 \sqrt{5}$ 中，最大的数是( )

A、 $- \sqrt{3}$ B、 $0$ C、 $2$ D、 $\sqrt{5}$

查看试题解析
2. 3个旅游团游客年龄的方差分别是：S_甲²=1.4，S_乙²=18.8，S_丙²=2.5，导游小方喜欢带游客年龄相近的团队，则他应该选择（　　）

A、甲团 B、乙团 C、丙团 D、哪一个都可以

查看试题解析
3. 下列计算正确的是( )

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 - \sqrt{2} = \sqrt{2}$ C、 $2 \times \sqrt{2} = \sqrt{4}$ D、 $2 \sqrt{2} - \sqrt{2} = \sqrt{2}$

查看试题解析
4. 下列说法正确的是( )

A、对角线互相垂直的平行四边形是正方形 B、一组对边平行另一组对边相等的四边形是平行四边形 C、一组对边平行且一组对角相等的四边形是平行四边形 D、对角线互相垂直的四边形是菱形

查看试题解析
5. $△ A B C$ 的三边分别为 $a$ ， $b$ ， $c$ ，下列条件：
$① ∠ A = ∠ B - ∠ C$ ； $② a^{2} = (b + c) (b - c)$ ； $③ a$ ： $b$ ： $c = 3$ ： $4$ ： $5$ ．
其中能判断 $△ A B C$ 是直角三角形的条件个数有( )

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
6. A、B、C、D、E五名学生在一次语文测验中的平均成绩是80分，而A、B、C三同学的平均成绩是78分，那么下列说法一定正确的是（　　）

A、D、E的成绩比其他三个都好 B、D、E两人的平均成绩是82分 C、最高分得主不是A、B、C、D D、D、E中至少有一个成绩不少于83分

查看试题解析
7. 如图，平行四边形 $A B C D$ 的周长为 $20 c m$ ， $A B \neq A D$ ， $A C$ 、 $B D$ 相交于点 $O$ ， $E O ⊥ B D$ 交 $A D$ 于点 $E$ ，则 $△ A B E$ 的周长为( )

A、 $8 c m$ B、 $10 c m$ C、 $12 c m$ D、 $20 c m$

查看试题解析
8. 关于函数 $y = - 2 x + 1$ ，下列结论正确的是( )

A、图形经过第一、二、三象限 B、当 $x > \frac{1}{2}$ 时， $y < 0$ C、 $y$ 随 $x$ 的增大而增大 D、图形必经过点 $(- 2,1)$

查看试题解析
9. 一个有进水管与出水管的容器，从某时刻开始 $4$ 分钟内只进水不出水，在随后 $8$ 分钟内既进水又出水 $.$ 每分钟的进水量和出水量是两个常数，容器内的水量 $y ($ 单位：升 $)$ 与时间 $x ($ 单位：分钟 $)$ 之间的关系如图所示，则每分钟出水量 $()$ 升．

A、 $2.5$ B、 $3.25$ C、 $3.75$ D、 $4$

查看试题解析
10. 如图， $∠ M O N = 90 °$ ，矩形 $A B C D$ 在 $∠ M O N$ 的内部，顶点 $A$ ， $B$ 分别在射线 $O M$ ， $O N$ 上， $A B = 4$ ， $B C = 2$ ，则点 $D$ 到点 $O$ 的最大距离是( )

A、 $2 \sqrt{2} + 2$ B、 $2 \sqrt{2} - 2$ C、 $2 \sqrt{5} - 2$ D、 $\sqrt{2} + 2$

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 二次根式 $\sqrt{3 - a}$ 有意义，则 $a$ 的取值范围是．

查看试题解析
12. 将直线 $y = - 2 x + 4$ 向下平移 $2$ 个单位，得到的直线解析式为．

查看试题解析
13. 某青年排球队 $12$ 名队员的年龄情况如下表：
年龄
$18$
$19$
$20$
$21$
$22$
人数
$1$
$x$
$y$
$2$
$2$
其中 $x > y$ ，中位数为 $20$ ，则这个队队员年龄的众数是．

查看试题解析
14. 如图，这是我国古代数学著作 $《$ 九章算术 $》$ 中的一个问题：一根竹子高 $1$ 丈，折断后竹子顶端落在离竹子底端 $3$ 尺处，折断处离地面的高度是尺 $(1$ 丈 $= 10$ 尺 $)$ ．

查看试题解析
15. 如图，已知在长方形ABCD中，将△ABE沿着AE折叠至△AEF的位置，点F在对角线AC上，若BE=3，EC=5，则线段CD的长是.

查看试题解析
16. 如图，点B、C分别在两条直线 $y = 2 x$ 和 $y = k x$ 上，点A、D是 $x$ 轴上两点，已知四边形ABCD是正方形，则k值为.

查看试题解析

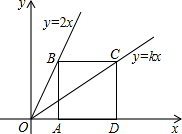
三、计算题：本大题共1小题，共8分。

17. 计算：

(1)、 $(\sqrt{24} - \sqrt{2}) - (\sqrt{8} + \sqrt{6})$

(2)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div \sqrt{2}$

查看试题解析

四、解答题：本题共7小题，共64分。解答应写出文字说明，证明过程或演算步骤。

18. 一次函数图象经过 $(- 2,1)$ 和 $(1,4)$ 两点，

(1)、求这个一次函数的解析式；

(2)、当 $x = 3$ 时，求 $y$ 的值．

查看试题解析
19. 如图， $A E / / B F$ ， $B D$ 平分 $∠ A B F$ ，且交 $A E$ 于点 $D$ ，过点 $D$ 作 $D C / / A B$ 交 $B F$ 于点 $C .$ 求证：四边形 $A B C D$ 是菱形．

查看试题解析
20. 为了绿化环境，某中学八 $(3)$ 班同学利用周末时间参加了植树活动，下面是今年 $3$ 月份该班每名同学植树株数情况的扇形统计图和不完整的条形统计图，请根据以下统计图中的信息解答下列问题 $.$

(1)、该班一共有多少名同学参加了植树活动？补全条形统计图；

(2)、扇形统计图中植树为“ $1$ 株”的扇形圆心角的度数为；该班同学植树株数的中位数是；

(3)、小明用以下方法计算出该班同学平均植树的株数是： $(1 + 2 + 3 + 4 + 5) \div 5 = 3 ($ 株 $)$ ，根据你所学的统计知识，判断小明的计算方法是否正确，若不正确，请写出正确的计算结果．

查看试题解析
21. 如图是三张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为 $1$ ，线段 $A C$ 的两个端点均在格点上 $($ 小正方形的顶点 $)$ ．

(1)、在图 $1$ 中，点 $O$ 在格点上，画出以 $A C$ 为边， $O$ 为对角线交点的平行四边形 $A C E F$ ；

(2)、在图 $2$ 中，点 $P$ 在格点上，作出点 $P$ 关于直线 $A C$ 的对称点 $Q$ ；

(3)、在图 $3$ 中，画出一个以线段 $A C$ 为对角线、面积为 $6$ 的矩形 $A B C D$ ，且点 $B$ 和点 $D$ 均在格点上 $. ($ 要求仅用无刻度的直尺画图，不写作法，保留画图痕迹 $)$

查看试题解析
22. 某商店分两次购进 $A$ 、 $B$ 两种商品进行销售，每次购进同一种商品的进价相同，具体情况如下表所示：

购进数量 $($ 件 $)$
所需费用 $($ 元 $)$

$A$

$B$
第一次
$30$
$40$
$3800$
第二次
$40$
$30$
$3200$

(1)、求 $A$ 、 $B$ 两种商品每件的进价分别是多少元？

(2)、为满足市场需求，商场在售完前期所有商品之后，决定再次以同样的价格购进 $A$ 、 $B$ 两种商品共 $1000$ 件，其中 $A$ 种商品的数量不少于 $B$ 种商品数量的 $4$ 倍，且 $A$ 种商品以每件 $30$ 元出售， $B$ 种商品以每件 $100$ 元出售 $.$ 请你为商场确定获得最大利润的进货方案，并求出最大利润．

查看试题解析
23. 如图，已知 $A D / / B C$ ， $A B ⊥ B C$ ， $A B = B C = 4$ ， $P$ 为线段 $A B$ 上一动点 $.$ 将 $△ B P C$ 沿 $P C$ 翻折至 $△ E P C$ ，延长 $C E$ 交射线 $A D$ 于点 $D$

(1)、如图 $1$ ，当 $P$ 为 $A B$ 的中点时，求出 $A D$ 的长．

(2)、如图 $2$ ，延长 $P E$ 交 $A D$ 于点 $F$ ，连接 $C F$ ，求证： $∠ P C F = 45 °$ ．

查看试题解析
24. 如图1，已知直线 $l_{1}$ ： $y = k x + 4$ 交 $x$ 轴于 $A (4 ， 0)$ ，交 $y$ 轴于 $B$ .

(1)、直接写出 $k$ 的值为.

(2)、如图2， $C$ 为 $x$ 轴负半轴上一点，过 $C$ 点的直线 $l_{2}$ ： $y = \frac{1}{2} x + n$ 经过 $A B$ 的中点 $P$ ，点 $Q (t ， 0)$ 为 $x$ 轴上一动点，过 $Q$ 作 $Q M ⊥ x$ 轴分别交直线 $l_{1}$ 、 $l_{2}$ 于 $M$ 、 $N$ ，且 $M N = 2 M Q$ ，求 $t$ 的值.

(3)、如图3，已知点 $M (- 1 ， 0)$ ，点 $N (5 m ， 3 m + 2)$ 为直线 $A B$ 右侧一点，且满足 $∠ O B M = ∠ A B N$ ，求点 $N$ 坐标.

查看试题解析

	购进数量 $($ 件 $)$		所需费用 $($ 元 $)$
	$A$	$B$	所需费用 $($ 元 $)$
第一次	$30$	$40$	$3800$
第二次	$40$	$30$	$3200$

年龄	$18$	$19$	$20$	$21$	$22$
人数	$1$	$x$	$y$	$2$	$2$