浙教版数学八上第1章章末重难点题型专训角平分线

试卷更新日期：2024-08-01 类型：单元试卷

进入出卷网下载

一、选择题

1. 如图，OD平分 $∠ A O B ， D E ⊥ A O$ 于点 $E ， D E = 3 ， F$ 是射线OB上的任一点，则DF的长度不可能是（）

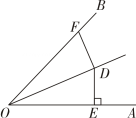A、2.8 B、3 C、4.2 D、5

查看试题解析
2. 如图，在 $△ A B C$ 中，根据尺规作图痕迹，下列说法不一定正确的是（）

A、 $A F = B F$ B、 $A E = \frac{1}{2} A C$ C、 $∠ D B F + ∠ D F B = 90 °$ D、 $∠ B A F = ∠ E B C$

查看试题解析
3. 如图，在△ABC中，BA=BC，∠B=80°，观察图中尺规作图的痕迹，则∠DCE的度数为（）

A、60° B、65° C、70° D、75°

查看试题解析
4. 如图，已知AB=AD，那么添加下列一个条件后，不能判定 $△ A B C ≌ △ A D C$ 的是（）

A、CB=CD B、 $∠ B A C = ∠ D A C$ C、 $∠ B C A = ∠ D C A$ D、 $∠ B = ∠ D = 90 °$

查看试题解析
5. 如图，Rt△ABC中，∠C=90°，用尺规作图法作出射线AE，AE交BC于点D，CD=2，P为AB上一动点，则PD的最小值为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于 $\frac{1}{2}$ DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝3，AB＝10，则△ABG的面积是（）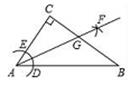

A、3 B、10 C、15 D、30

查看试题解析
7. 如图，在锐角△ABC中，∠BAC=45°，AB=2，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（）

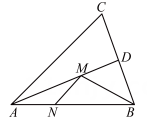A、1 B、 $\sqrt{2}$ C、1.5 D、

查看试题解析
8. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点 G作EF ∥ BC交AB于E，交AC 于F，过点G作 GD⊥AC 于D，下列四个结论：① EF=BE+CF；②∠BGC=90°+ $\frac{1}{2}$ ∠A ；③点G到 △ABC 各边的距离相等；④设GD=m，AE+AF=n，则 =mn. 其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 已知： $∠ A O B$ ．求作： $∠ A O B$ 的平分线．
作法：（1）以点 $O$ 为圆心，适当长为半径画弧，交 $O A$ 于点 $M$ ，交 $O B$ 于点 $N$ ；（2）分别以点 $M$ ， $N$ 为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧在 $∠ A O B$ 的内部相交于点 $P$ ；（3）画射线 $O P$ ，射线 $O P$ 即为所求（如图）．
从上述作法中可以判断 $△ M O P ≌ △ N O P$ ，其依据是（在“SSS”“SAS”“AAS”“ASA”中选填）

查看试题解析
10. 如图， $∠ A O E = ∠ C O E = 30 °$ ， $E C ⊥ O B$ 于点C ，若 $C E = 2$ ，则点E到OA的距离为．

查看试题解析
11. $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 12$ ，以点A为圆心，适当长为半径画弧，交 $A C$ 、 $A B$ 于点M、N ，再分别以M、N为圆心，大于 $\frac{1}{2} M N$ 为半径画弧，两弧交于点F ，作射线 $A F$ 交边 $B C$ 于点D ，已知 $A D = 13$ ， $△ A B D$ 的面积为40，则 $A B =$ ．

查看试题解析
12. 如图，射线 $O E$ 是 $∠ A O B$ 的平分线，C是射线 $O E$ 上一点， $C F ⊥ O A$ 于点F ．若D是射线 $O B$ 上一点，且 $O D = C F = 3$ ，则 $△ O D C$ 的面积是．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以顶点A为圆心，适当长为半径画弧，分别交 $A C ， A B$ 于点M ， N ，再分别以点M，N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P ，作射线 $A P$ 交边 $B C$ 于点D ，若 $C D = 3 ， A B = 10$ ，则 $△ A B D$ 的面积是．

查看试题解析
14. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是.

查看试题解析
15. 如图， $O D$ 平分 $∠ A O B$ ， $D E ⊥ A O$ 于点 $E$ ， $D E = 4.2$ ， $F$ 是射线 $O B$ 上的任一点，则 $D F$ 的长度不可能是（）

A、4.2 B、5.15 C、3.69 D、8

查看试题解析
16. 如图，已知∠AOB=30°，P是∠AOB平分线上一点，CP∥OB，交OA于点C，PD⊥OB，垂足为点D，且PC=4，则PD等于．

查看试题解析

三、解答题

17. 古人诗云：“草长莺飞二月天，拂堤杨柳醉春烟。儿童散学归来早，忙趁东风放纸鸢。”纸鸢，又称风筝，其制作技艺是我国民间的传统工艺，某班数学兴趣小组根据风筝的形状画出图形（如图所示），已知 $A B = B C$ ， $∠ A B D = ∠ C B D$ ，求证： $A D = C D$ ．

查看试题解析
18. 如图，AB是 $∠ C A D$ 的平分线， $A C = A D$ ，求证： $∠ C = ∠ D$ ．

查看试题解析
19. 如图，已知 $A B ∥ C D$ ， $∠ A B D = 4 0^{∘}$ ， $B E$ 平分 $∠ A B C$ ，且交 $C D$ 于点 $D$ ，则 $∠ C$ 的度数为．

查看试题解析
20. 在 $△ A B C$ 中， $∠ A C B$ 和 $∠ C A B$ 的角平分线 $C E 、 A D$ 相交于点 $G$ ．

(1)、若 $∠ B = 50 °$ ，求 $∠ A G C$ 的度数；

(2)、延长 $C E$ 至点 $N$ ，过点 $N$ 作 $B C$ 的平行线 $N M$ 交 $A B$ 于点 $M$ ，若 $E G = E M$ ，求证： $A C = A E + E N$ ．

查看试题解析
21.
综合与实践

(1)、【动手实验】数学课上，老师带领同学们对角的平分线的性质进行探究：
同学们任意作一个 $∠ A O B$ ，作出 $∠ A O B$ 的平分线 $O C .$ 在 $O C$ 上任取一点 $P$ ，过点 $P$ 画出 $O A$ ， $O B$ 的垂线，分别记垂足为 $D$ ， $E$ ，测量 $P D$ ， $P E .$ 第一小组的测量结果如下：
学生
$P D (c m)$
$P E (c m)$
学生
$P D (c m)$
$P E (c m)$
小明
$0.5$
$0.5$
小刚
$1.1$
$1.1$
小红
$0.8$
$0.8$
小丽
$1.3$
$1.3$
通过以上测量，你发现了角的平分线的什么性质？

(2)、【推理证明】请结合图 $1$ ，利用三角形全等证明这个性质．
如图1，已知： $∠ A O C = ∠ B O C$ ，点 $P$ 在 $O C$ 上， $P D ⊥ O A$ ， $P E ⊥ O B$ ，垂足分别为 $D$ ， $E .$ 求证： $P D = P E$ ．

(3)、【定理应用】如图2，点 $P$ 是 $∠ A O C$ 的角平分线上一点， $P D ⊥ O A$ ，垂足为点 $D$ ，且 $P D = 3$ ，点 $M$ 是射线 $O C$ 上一动点，求 $P M$ 的最小值．

查看试题解析

学生	$P D (c m)$	$P E (c m)$	学生	$P D (c m)$	$P E (c m)$
小明	$0.5$	$0.5$	小刚	$1.1$	$1.1$
小红	$0.8$	$0.8$	小丽	$1.3$	$1.3$

浙教版数学八上第1章章末重难点题型专训 角平分线

一、选择题

二、填空题

三、解答题

浙教版数学八上第1章章末重难点题型专训角平分线