浙教版数学八上第1章 三角形的初步知识 三阶单元测试卷
试卷更新日期:2024-08-01 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 如图,已知 ,下列所给条件不能证明△ ≌△ 的是( )
 A、 B、 C、 D、2. 如图,中, , 点O是垂直平分线的交点,则的度数为( )
A、 B、 C、 D、2. 如图,中, , 点O是垂直平分线的交点,则的度数为( ) A、 B、 C、 D、3. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,64. 已知一条线段AB外有一点C , 利用尺规过点C作线段AB的垂线,以下作法正确的是( )A、
A、 B、 C、 D、3. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,64. 已知一条线段AB外有一点C , 利用尺规过点C作线段AB的垂线,以下作法正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( )
5. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( ) A、5 B、5.5 C、6 D、76. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A、5 B、5.5 C、6 D、76. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )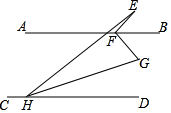 A、90° B、95° C、100° D、150°7. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A、90° B、95° C、100° D、150°7. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )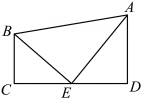 A、BC+AD=CD B、E为CD中点 C、∠AEB=90° D、S△ABE=S四边形ABCD8. 平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是()
A、BC+AD=CD B、E为CD中点 C、∠AEB=90° D、S△ABE=S四边形ABCD8. 平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形(如图),则d可能是()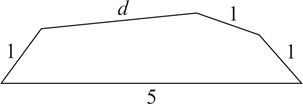 A、1 B、2 C、7 D、89. 如图:已知 , 度, 度,则 等于( )度.
A、1 B、2 C、7 D、89. 如图:已知 , 度, 度,则 等于( )度.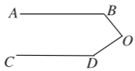 A、50 B、60 C、80 D、9010. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB , 其中正确的有( )
A、50 B、60 C、80 D、9010. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , 则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB , 其中正确的有( )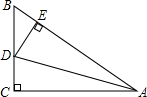 A、2个 B、3个 C、4个 D、1个
A、2个 B、3个 C、4个 D、1个二、填空题(本题有6小题,每小题4分,共24分)
-
11. 在△ABC中,AC=5,中线AD=7,则AB边的取值范围是.12. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
 13. 如图,中, , , 是的角平分线, , 则的最大值为 .
13. 如图,中, , , 是的角平分线, , 则的最大值为 . 14. 如图,在△ABC中,CB>CA,∠BAC=80°,D为AB上一点,满足CB-CA=BD,I为△ABC三条角平分线的交点连接ID,则∠IDA=.
14. 如图,在△ABC中,CB>CA,∠BAC=80°,D为AB上一点,满足CB-CA=BD,I为△ABC三条角平分线的交点连接ID,则∠IDA=. 15. 如图,在中, , , 的平分线与的垂直平分线交于点 , 将沿在上,在上折叠,点与点恰好重合,则为度.
15. 如图,在中, , , 的平分线与的垂直平分线交于点 , 将沿在上,在上折叠,点与点恰好重合,则为度. 16. 如图,在中, , 角平分线、交于点 , 于点下列结论:
16. 如图,在中, , 角平分线、交于点 , 于点下列结论:
::;
;
;
,
其中正确结论是 .
三、解答题(本题共8小题,第17题7分,第18题9分,第19题9分,第20题6分,第21题9分,第22题8分,第23题8分,第24题10分,共66分)
-
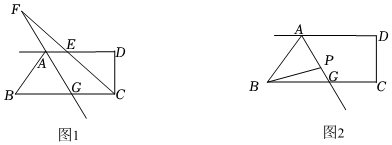
17. 如图1,已知AB//CD , P是直线AB , CD外的一点,PF⊥CD于点F , PE交AB于点E , 满足∠FPE=60°.
 (1)、求∠AEP的度数;(2)、如图2,射线PN从PE出发,以每秒10°的速度绕P点按逆时针方向匀速旋转,当PN到达PF时立刻返回至PE , 然后继续按上述方式旋转;射线EM从EA出发,以每秒9°的速度绕E点按顺时针方向旋转至EP后停止运动,此时射线PN也停止运动.若射线PN、射线EM同时开始运动,设运动时间为t秒.
(1)、求∠AEP的度数;(2)、如图2,射线PN从PE出发,以每秒10°的速度绕P点按逆时针方向匀速旋转,当PN到达PF时立刻返回至PE , 然后继续按上述方式旋转;射线EM从EA出发,以每秒9°的速度绕E点按顺时针方向旋转至EP后停止运动,此时射线PN也停止运动.若射线PN、射线EM同时开始运动,设运动时间为t秒.①当射线PN平分∠EPF时,求∠AEM的度数;
②当直线EM与直线PN平行时,求t的值.
18. 定义:从的顶点出发,在角的内部作一条射线,若该射线将分得的两个角中有一个角与互为补角,则称该射线为的“好线”.如图,点O在直线AB上,OC、OD在直线AB上方,且 , 射线OE是的“好线”.
 (1)、若 , 且OE在内部,求的度数;(2)、若OE恰好平分 , 求的度数;(3)、若OF是的平分线,OG是的平分线,直接写出与的数量关系.19. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.
(1)、若 , 且OE在内部,求的度数;(2)、若OE恰好平分 , 求的度数;(3)、若OF是的平分线,OG是的平分线,直接写出与的数量关系.19. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.经过组内合作交流,小明得到了如下的解决方法:延长到点E , 使.请根据小明的方法思考:
 (1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.
(1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.如图2,已知 , , , P为的中点.若A , C , D共线,求证:平分;
20. 【综合实践活动】【问题背景】
小亮想测量他家门口水塘两个端点A , B长度(如图1),但是小亮找不足够长度的的绳子,小亮寻求哥哥的帮助.
【理论准备】
哥哥帮他出了这样一个方法:先在地上取一个可以直接到达A点和B点的点C , 连接并延长到D , 使;连接并延长到E , 使 , 连接并测量出它的长度(如图2),请你帮小亮说明的长度等于水塘两个端点长度的原因;

【实际操作】
小亮实际测量时发现但是由于房屋的阻挡,无法采用上述的方法进行测量,哥哥提出仍然可以计算出长度(如图3),方法如下:
⑴在房屋M墙边找一点C , 使得;
⑵在院子里找一点E , 使得:此时发现;
⑶测量出B到房屋M墙的距离 , 即: , ;
⑷测量出A到的距离 , 即:AE⊥CE , , 同时发现;
经过以上的方法可以计算出的长度.
请根据哥哥的思路提示,帮助小亮完成计算出的长度:
解:如图4,延长至F , 使得 , 连接 .
……
 (1)、【成果迁移】
(1)、【成果迁移】如图5,海警船甲在指挥中心(A处)北偏西的B处,一艘可疑船只乙在指挥中心正东方向的C处,并且两艘船到指挥中心A的距离相等(),可疑船只沿北偏东的方向以20海里/小时的速度行驶,指挥中心命令海警船甲从B点向正东方向以30海里/小时的速度追击,两船前进3小时后,指挥中心观测到甲、乙两船分别到达D , E处,且两船和指挥中心形成的夹角为 , (),请直接写出此时甲、乙两船之间的距离 .
 21. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE.
21. 如图,等腰Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连接AE,作AF⊥AE且AF=AE. (1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .22.(1)、学习了平行线后,王玲同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如下:
(1)、如图1,过F点作FG⊥AC交于G点,求证:AG=EC;(2)、如图2,连接BF交AC于G点,若AC=BC=4,AG=3,求证:E点为BC中点;(3)、如图3,当E点在CB的延长线上时,连接BF与AC的延长线交于D点,若 , 求的值是 .22.(1)、学习了平行线后,王玲同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如下:
①请你仿照以上过程,在下图中画出一条直线b,使直线b经过点P,且b∥a,要求保留折纸痕迹,画出所用到的直线,无需写画法.
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 ▲ 线.
 (2)、已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
(2)、已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
求证:BE∥CF.
要求:请你阅读小宁同学如下的证明过程,圈出他证明中的不符合题意,并在右侧的空白处进行改正,若有跳步,请在下面方框内补充完整并将其标记到证明过程中的相应位置,可如下所示使用修改替换符号:“
 ”
”证明:∵AB∥CD

∴∠ABC=∠BCD(同位角相等,两直线平行).两直线平行,内错角相等.
∵BE平分∠ABC,CE平分∠BCD(已知),
∴∠2=∠3(角平分线的定义).
∴BE∥CF(两直线平行,内错角相等)