浙教版数学八上第1章 三角形的初步知识 二阶单元测试卷
试卷更新日期:2024-08-01 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 如图,点B,E,C,F四点在同一条直线上,AC∥DF,AC =DF,添加一个条件,不能判定△ABC≌△DEF的是( )
 A、BE=CF B、AB=DE C、∠B=∠DEF D、∠A=∠D2. 如图,已知分别平分 , 若 , 则的大小为( )
A、BE=CF B、AB=DE C、∠B=∠DEF D、∠A=∠D2. 如图,已知分别平分 , 若 , 则的大小为( ) A、 B、 C、 D、3. 如图,在△ACB中,∠C=90°, AB的垂直平分线交AB、AC于点M、N,若AC=8,BC=4,则NC的长度为( ).
A、 B、 C、 D、3. 如图,在△ACB中,∠C=90°, AB的垂直平分线交AB、AC于点M、N,若AC=8,BC=4,则NC的长度为( ). A、2 B、3 C、4 D、54. 如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,使集贸市场到三条公路的距离相等,则这个集贸市场应建在( )
A、2 B、3 C、4 D、54. 如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,使集贸市场到三条公路的距离相等,则这个集贸市场应建在( ) A、在AC、BC两边高线的交点处 B、在AC、BC两边中线的交点处 C、在、两内角平分线的交点处 D、在AC、BC两边垂直平分线的交点处5. 如图,在四边形ABCD中, , 若对角线BD平分 , 则的面积为( )
A、在AC、BC两边高线的交点处 B、在AC、BC两边中线的交点处 C、在、两内角平分线的交点处 D、在AC、BC两边垂直平分线的交点处5. 如图,在四边形ABCD中, , 若对角线BD平分 , 则的面积为( ) A、10 B、24 C、15 D、126. 如图,已知直线 , 平分 , , 则的度数是( )
A、10 B、24 C、15 D、126. 如图,已知直线 , 平分 , , 则的度数是( )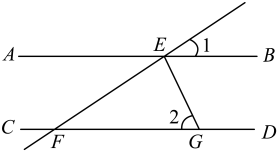 A、 B、 C、 D、7. 阅读以下作图步骤:
A、 B、 C、 D、7. 阅读以下作图步骤:①在和上分别截取 , 使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线 , 连接 , 如图所示.根据以上作图,一定可以推得的结论是( )
 A、且 B、且 C、且 D、且8. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( ).
A、且 B、且 C、且 D、且8. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( ). A、1m B、1.6m C、1.8m D、1.4m9. 如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为( )
A、1m B、1.6m C、1.8m D、1.4m9. 如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为( )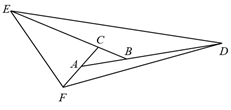 A、2 B、3 C、4 D、510. 如图,中, , , 三条角平分线、、交于 , 于下列结论:;;平分;其中正确的结论个数有( )
A、2 B、3 C、4 D、510. 如图,中, , , 三条角平分线、、交于 , 于下列结论:;;平分;其中正确的结论个数有( )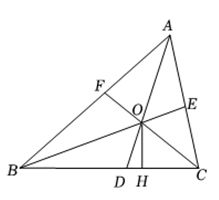 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图,AD是△ABC的角平分线,若 , 则 .
 12. 如图,是一个测量工件内槽宽的工具,点O既是AA'的中点,也是BB'的中点,若测得AB=3.5 cm,则该内槽A'B'的宽为cm.
12. 如图,是一个测量工件内槽宽的工具,点O既是AA'的中点,也是BB'的中点,若测得AB=3.5 cm,则该内槽A'B'的宽为cm. 13. 如图:小文在一个周长为22cm的△ABC中,截出了一个周长为14cm的△ADC , 发现点D刚好落在AB的垂直平分线上,请问AB的长是cm
13. 如图:小文在一个周长为22cm的△ABC中,截出了一个周长为14cm的△ADC , 发现点D刚好落在AB的垂直平分线上,请问AB的长是cm 14. 如图,在中,于E , 于F , AD为的平分线,的面积是28cm2 , , , cm.
14. 如图,在中,于E , 于F , AD为的平分线,的面积是28cm2 , , , cm. 15. 如图,△ABC是三条边不相等的三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,最多可以画出个这样的三角形.
15. 如图,△ABC是三条边不相等的三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,最多可以画出个这样的三角形. 16. 如图, 与 中,AB=AE , BC=EF , ∠B=∠E , AB交EF于D . 给出下列结论:①∠AFC=∠C;②DF=CF;③FA是∠DFC的平分线;④∠BFD=∠CAF . 其中正确的结论是:(填写所有正确结论的序号).
16. 如图, 与 中,AB=AE , BC=EF , ∠B=∠E , AB交EF于D . 给出下列结论:①∠AFC=∠C;②DF=CF;③FA是∠DFC的平分线;④∠BFD=∠CAF . 其中正确的结论是:(填写所有正确结论的序号).
三、解答题(本题共8小题,第17题6分,第18题6分,第19题6分,第20题9分,第21题9分,第22题9分,第23题11分,第24题10分,共66分)
-
17. 如图是一种躺椅及其结构示意图,扶手AB与底座CD都平行于地面EF , 前支架OE与后支架OF分别与CD交于点G和点D , AB与DM交于点N , ∠AOE=∠BNM .
 (1)、请对说明理由;(2)、若OE平分∠AOF , ∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.18. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 .
(1)、请对说明理由;(2)、若OE平分∠AOF , ∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.18. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 . (1)、求证:平分;(2)、若 , 求的面积.19. 如图所示,已知∠B=90°,△ADC是以CD为底边的等腰直角三角形,过点D作AB的垂线交AB于点E.
(1)、求证:平分;(2)、若 , 求的面积.19. 如图所示,已知∠B=90°,△ADC是以CD为底边的等腰直角三角形,过点D作AB的垂线交AB于点E. (1)、试说明:△ABC≌△DEA;(2)、若BE=5,CB=4,求DE的长.20. 【阅读】如图1,光线从空气中射入玻璃砖时,光线的传播方向发生了改变,即玻璃砖中的光线与原来空气中的光线不在同一条直线上,这是光线在玻璃砖中的折射现象.
(1)、试说明:△ABC≌△DEA;(2)、若BE=5,CB=4,求DE的长.20. 【阅读】如图1,光线从空气中射入玻璃砖时,光线的传播方向发生了改变,即玻璃砖中的光线与原来空气中的光线不在同一条直线上,这是光线在玻璃砖中的折射现象.【探究】为了探究光折射时的特点,科学实验小组将一束光斜射到一块玻璃砖的上表面上的点处,并在下表面()的点处射出,于点 , 如图2所示,图中所有的点都在同一平面内,查问相关科学知识,得到 .
 (1)、若 , , 求光的传播方向改变了多少度;(2)、请判断射入光线与射出光线是否平行,并说明理由;(3)、已知光线与的夹角为35°,如图3所示.若射出光线与光线垂直,则的度数为 .21. [阅读理解]课外兴趣小组活动时,老师提出了如下问题:
(1)、若 , , 求光的传播方向改变了多少度;(2)、请判断射入光线与射出光线是否平行,并说明理由;(3)、已知光线与的夹角为35°,如图3所示.若射出光线与光线垂直,则的度数为 .21. [阅读理解]课外兴趣小组活动时,老师提出了如下问题:如图1,在中,若 , 求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD到点E , 使 , 连结BE , 请根据小明的方法思考:
图1
 图2
图2  图3
图3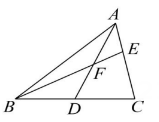 (1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .22. 如图,平面直角坐标系内,直线交x轴于点A , 交y轴于点B , 直线于点D , 交y轴于点E , 交x轴于点C , , 且 .
(1)、由已知和作图能得到 , 其理由是什么?(2)、求AD的取值范围.(3)、如图3,AD是的中线,BE交AC于点F , 且 , 试说明 .22. 如图,平面直角坐标系内,直线交x轴于点A , 交y轴于点B , 直线于点D , 交y轴于点E , 交x轴于点C , , 且 . (1)、求证:;(2)、求的面积;(3)、点M为线段上一动点,作 , 且交于点N , 当点M运动时,的值是否变化?若不变,求出其值;若变化,请说明理由.23. 探索角的平分线的画法.(1)、画法1:利用直尺和圆规
(1)、求证:;(2)、求的面积;(3)、点M为线段上一动点,作 , 且交于点N , 当点M运动时,的值是否变化?若不变,求出其值;若变化,请说明理由.23. 探索角的平分线的画法.(1)、画法1:利用直尺和圆规请在图中用直尺和圆规画出 的平分线 ;(不写画法不需证明,保留作图痕迹)
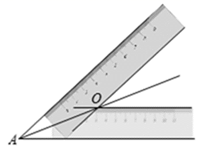
 (2)、画法2:利用等宽直尺.
(2)、画法2:利用等宽直尺.如图,将一把等宽直尺的一边依次落在 的两条边上,再过另一边分别画直线,两条直线相交于点O.画射线 ,则射线 是 的平分线.这种角的平分线的画法依据的是______.
 A、 B、 C、 D、(3)、画法3:利用刻度尺
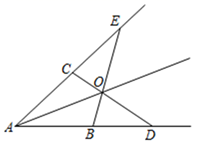
A、 B、 C、 D、(3)、画法3:利用刻度尺已知:如图,在 的两条边上分别画 , ,连接 、 ,交点为点O,画射线 .
求证: 是 的平分线.
 (4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明.
(4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明. 24. 如图,中, , , E点为射线上一动点,连结 , 作且 .
24. 如图,中, , , E点为射线上一动点,连结 , 作且 . (1)、如图1,过F点作交于D点,求证:;(2)、如图2,连结交于G点,若 , , 求证:E点为中点.(3)、当E点在射线上,连结与直线交于G点,若 , , 则 . (直接写出结果)
(1)、如图1,过F点作交于D点,求证:;(2)、如图2,连结交于G点,若 , , 求证:E点为中点.(3)、当E点在射线上,连结与直线交于G点,若 , , 则 . (直接写出结果)