浙教版数学八上第1章 三角形的初步知识 一阶单元测试卷
试卷更新日期:2024-08-01 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 如图,平分 , 点P在上, , , 则点P到的距离是( )
 A、4 B、3 C、2 D、12. 下列命题中,是真命题的是( )A、相等的角是对顶角 B、内错角相等,两直线平行 C、同旁内角互补 D、垂直于同一直线的两直线平行3. 如图, , , , 则的度数是( )
A、4 B、3 C、2 D、12. 下列命题中,是真命题的是( )A、相等的角是对顶角 B、内错角相等,两直线平行 C、同旁内角互补 D、垂直于同一直线的两直线平行3. 如图, , , , 则的度数是( ) A、 B、 C、 D、4. 如图,下面是三位同学的折纸示意图,则AD依次是的( )
A、 B、 C、 D、4. 如图,下面是三位同学的折纸示意图,则AD依次是的( ) A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、中线、高线 D、角平分线、高线、中线5. 以下列各组线段为边,能组成三角形的是( )A、2cm、10cm、13cm B、3cm、7cm、4cm C、4cm、4cm、4cm D、5cm、14cm、6cm6. 如图,AD//BC , BD平分∠ABC , ∠D=50°,∠C=34°,则∠CAB的度数为( )
A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、中线、高线 D、角平分线、高线、中线5. 以下列各组线段为边,能组成三角形的是( )A、2cm、10cm、13cm B、3cm、7cm、4cm C、4cm、4cm、4cm D、5cm、14cm、6cm6. 如图,AD//BC , BD平分∠ABC , ∠D=50°,∠C=34°,则∠CAB的度数为( ) A、46° B、50° C、56° D、68°7. 如图,已知在△ABC和△DEF中, , , 点B、F、C、E在同一条直线上,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
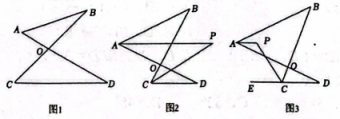
A、46° B、50° C、56° D、68°7. 如图,已知在△ABC和△DEF中, , , 点B、F、C、E在同一条直线上,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( ) A、 B、 C、 D、8. 某同学打算制作简易工具来测量物体表面的倾斜程度,其方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的90°刻度线与三角板的底边平行.接着将用细线和铅锤做成的重锤线顶端固定在量角器中心点O处.现将三角板底边紧贴被测物体表面,如题4图所示,此时重锤线在量角器上对应的刻度为35°,那么被测物体表面的倾斜角α为( )
A、 B、 C、 D、8. 某同学打算制作简易工具来测量物体表面的倾斜程度,其方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的90°刻度线与三角板的底边平行.接着将用细线和铅锤做成的重锤线顶端固定在量角器中心点O处.现将三角板底边紧贴被测物体表面,如题4图所示,此时重锤线在量角器上对应的刻度为35°,那么被测物体表面的倾斜角α为( ) A、15° B、30° C、35° D、55°9. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( )
A、15° B、30° C、35° D、55°9. 如图,中,分别是其角平分线和中线,过点C作于F , 连接 , 则线段的长为( ) A、 B、2 C、 D、310. 如图,在和中, , , , , 连接 , , 延长交于点F , 连接 . 下列结论:①;②;③;④平分 . 其中正确的结论个数有( )个.
A、 B、2 C、 D、310. 如图,在和中, , , , , 连接 , , 延长交于点F , 连接 . 下列结论:①;②;③;④平分 . 其中正确的结论个数有( )个. A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图,△ABC中,D是AB上一点,CF∥AB , D、E、F三点共线,请添加一个条件 , 使得AE=CE . (只添一种情况即可)
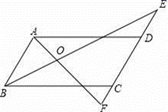
 12. 有三面镜子如图放置,其中镜子 和 相交所成的角 ,已知入射光线 经 反射后,反射光线与入射光线 平行,若 ,则镜子 和 相交所成的角 . (结 果用含 的代数式表示)
12. 有三面镜子如图放置,其中镜子 和 相交所成的角 ,已知入射光线 经 反射后,反射光线与入射光线 平行,若 ,则镜子 和 相交所成的角 . (结 果用含 的代数式表示) 13. 如图中, , 平分 , , , 则的面积是.
13. 如图中, , 平分 , , , 则的面积是. 14. 将常用的三角板如图所示放置,其中 , C点为边所在直线上一定点(点C在点O的左边),点D为直线上一动点(不与C、B重合),平分 , 平分 . 若 , 则 . (用含α的式子表示)
14. 将常用的三角板如图所示放置,其中 , C点为边所在直线上一定点(点C在点O的左边),点D为直线上一动点(不与C、B重合),平分 , 平分 . 若 , 则 . (用含α的式子表示) 15. 已知AB∥CD,点E在直线AB上,以点E为顶点作∠FEG=90°,点F在直线AB上方,点G在直线CD下方,EG与CD交于点N,作∠BEF的角平分线并反向延长与∠CNE的角平分线交于点P,则∠P的度数为 .16. 如图,在中, , 以AC为边,作 , 满足 , 点E为BC上一点,连接AE , , 连接DE . 下列结论中正确的是 . (填序号)
15. 已知AB∥CD,点E在直线AB上,以点E为顶点作∠FEG=90°,点F在直线AB上方,点G在直线CD下方,EG与CD交于点N,作∠BEF的角平分线并反向延长与∠CNE的角平分线交于点P,则∠P的度数为 .16. 如图,在中, , 以AC为边,作 , 满足 , 点E为BC上一点,连接AE , , 连接DE . 下列结论中正确的是 . (填序号)①;②;③若 , 则;④ .

三、解答题(本题共8小题,第17题6分,第18题7分,第19题6分,第20题9分,第21题9分,第22题6分,第23题9分,第24题14分,共66分)
-
17. 如图,已知 , 请用尺规过点作一条直线,使其将分成面积比为两部分.(保留作图痕迹,不写作法)
 18. 已知:如图,点D , E , F分别是三角形ABC的边BC , CA , AB上的点,DF∥CA , ∠FDE=∠A;
18. 已知:如图,点D , E , F分别是三角形ABC的边BC , CA , AB上的点,DF∥CA , ∠FDE=∠A; (1)、求证:DE∥BA .(2)、若∠BFD=∠BDF=2∠EDC , 求∠B的度数.19. 如图,中, , D是BA延长线上一点,点E是∠CAD的平分线上一点,过点E作EF⊥AC于F , EG⊥AD于G .
(1)、求证:DE∥BA .(2)、若∠BFD=∠BDF=2∠EDC , 求∠B的度数.19. 如图,中, , D是BA延长线上一点,点E是∠CAD的平分线上一点,过点E作EF⊥AC于F , EG⊥AD于G . (1)、求证:;(2)、若 , , , 求AF的长.20. 【探究学习】小学阶段,我们可以通过“拼”角、“折”角,观察得到三角形内角和为180°.现在我们学习了平行线的性质,就可以证明此结论的正确性了.
(1)、求证:;(2)、若 , , , 求AF的长.20. 【探究学习】小学阶段,我们可以通过“拼”角、“折”角,观察得到三角形内角和为180°.现在我们学习了平行线的性质,就可以证明此结论的正确性了. (1)、如图1,过的顶点A作BC的平行线ED , 请你证明三角形的内角和为180°;
(1)、如图1,过的顶点A作BC的平行线ED , 请你证明三角形的内角和为180°;【解题反思】平行线具有“等角转化”的功能.
(2)、【迁移应用】健康骑行越来越受到老百姓的喜欢,自行车的示意图如图2,其中 .①若 , , 则的度数为_▲_;
②若 , , 求的度数.
(3)、如图3,若 , 点P在AB , CD外部,请直接写出 , , 之间的关系.21. 在直线m上依次取互不重合的三个点D , A , E , 在直线m上方有 , 且满足 .(1)、【积累经验】如图1,当时,猜想线段DE , BD , CE之间的数量关系是;
 (2)、【类比迁移】
(2)、【类比迁移】如将2,当时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;
 (3)、【拓展应用】
(3)、【拓展应用】如图3,在中,是钝角, , , , 直线m与CB的延长线交于点F , 若 , 的面积是12,请直接写出与的面积之和.
 22. 两个大小不同的等腰直角三角板如图所示放置,右图是由它抽象出的几何图形,B , C , E在同一条直线上,连接DC .
22. 两个大小不同的等腰直角三角板如图所示放置,右图是由它抽象出的几何图形,B , C , E在同一条直线上,连接DC .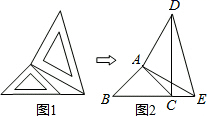 (1)、求证:△ABE≌△ACD;(2)、若图2中的BE=3CE , CD=6,求 △DCE的面积.
(1)、求证:△ABE≌△ACD;(2)、若图2中的BE=3CE , CD=6,求 △DCE的面积.