【培优版】浙教版数学八上1.5三角形全等的判定 同步练习
试卷更新日期:2024-08-01 类型:同步测试
一、选择题
-
1.
如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
 A、330° B、315° C、310° D、320°2. 如图,OP是的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定的是( )
A、330° B、315° C、310° D、320°2. 如图,OP是的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定的是( ) A、 B、 C、 D、3. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( )
A、 B、 C、 D、3. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( ) A、 B、 C、 D、不能确定4. 如图所示,在△ABC中,AB=8,点M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于F , 已知CF=10,则AC的长为( )
A、 B、 C、 D、不能确定4. 如图所示,在△ABC中,AB=8,点M是BC的中点,AD是∠BAC的平分线,作MF∥AD交AC于F , 已知CF=10,则AC的长为( ) A、12 B、11 C、10 D、95. 已知AD是△ABC中BC边上的中线,AB=10,AC=6,则AD的取值范围是( )A、4<AD<16 B、2<AD<8 C、4<AD<10 D、8≤AD≤166. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( )
A、12 B、11 C、10 D、95. 已知AD是△ABC中BC边上的中线,AB=10,AC=6,则AD的取值范围是( )A、4<AD<16 B、2<AD<8 C、4<AD<10 D、8≤AD≤166. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( ) A、①③ B、①②④ C、①②③ D、②③7. 如图,在中,和的平分线 , 相交于点O,交于E,交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的个数是( )
A、①③ B、①②④ C、①②③ D、②③7. 如图,在中,和的平分线 , 相交于点O,交于E,交于F,过点O作于D,下列三个结论:①;②当时,;③若 , , 则 . 其中正确的个数是( )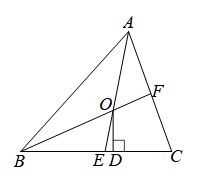 A、1个 B、2个 C、3个 D、0个8. 如图,是的中线,过点D作 , 交于点E,是的角平分线,点M在边上,且 , 点N在线段上,若 , 记的面积为 , 的面积为 , 则的值为( )
A、1个 B、2个 C、3个 D、0个8. 如图,是的中线,过点D作 , 交于点E,是的角平分线,点M在边上,且 , 点N在线段上,若 , 记的面积为 , 的面积为 , 则的值为( )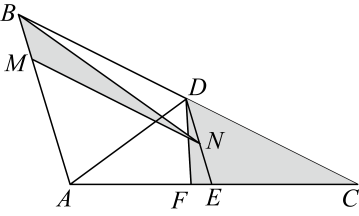 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,中, , AD平分交BC于点D,E为线段AC上一点,连接DE,且.若 , , 则AE的长为.
 10. 如图,且且 , 请按图中标注的数据,计算图中实线所围成的图形的面积 .
10. 如图,且且 , 请按图中标注的数据,计算图中实线所围成的图形的面积 . 11. 如图,的面积为10,、分别是 , 上的点,且 , .连接 , 交于点 , 连接并延长交于点.则四边形的面积为.
11. 如图,的面积为10,、分别是 , 上的点,且 , .连接 , 交于点 , 连接并延长交于点.则四边形的面积为. 12. 如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等.
12. 如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等.
三、解答题
-
13. 如图,已知直线 .
 (1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则__________;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当_________秒时, .14. 如图, , , 平分交于点 .
(1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则__________;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当_________秒时, .14. 如图, , , 平分交于点 . (1)、求的度数;(2)、若 , 判断与的位置关系,并说明理由.15. 如图,直线AB∥CD , 直线EF与AB、CD分别交于点G、H , ∠EHD=α(0°<α<90°).小安将一个含30°角的直角三角板PMN按如图①放置,使点N、M分别在直线AB、CD上,且在点G、H的右侧,∠P=90°,∠PMN=60°.
(1)、求的度数;(2)、若 , 判断与的位置关系,并说明理由.15. 如图,直线AB∥CD , 直线EF与AB、CD分别交于点G、H , ∠EHD=α(0°<α<90°).小安将一个含30°角的直角三角板PMN按如图①放置,使点N、M分别在直线AB、CD上,且在点G、H的右侧,∠P=90°,∠PMN=60°. (1)、填空:∠PNB+∠PMD ∠P(填“>”“<”或“=”);(2)、若∠MNG的平分线NO交直线CD于点O , 如图②.
(1)、填空:∠PNB+∠PMD ∠P(填“>”“<”或“=”);(2)、若∠MNG的平分线NO交直线CD于点O , 如图②.①当NO∥EF , PM∥EF时,求α的度数;
②小安将三角板PMN保持PM∥EF并向左平移,在平移的过程中求∠MON的度数(用含α的式子表示).
四、实践探究题
-
16.
 (1)、【基础巩固】如图 1,在 与 中, ,求证: ;(2)、【尝试应用】如图 2,在 与 中, 三 点在一条直线上, 与 交于点 ,若点 为 中点,
(1)、【基础巩固】如图 1,在 与 中, ,求证: ;(2)、【尝试应用】如图 2,在 与 中, 三 点在一条直线上, 与 交于点 ,若点 为 中点,① 求 的大小;
② ,求 的面积;
(3)、【拓展提高】如图 3, 与 中, 与 交于 点 的面积为 32,求 的长.17. 小明在学习中遇到了问题:如图①,在中, , , D为BC边上的中点,求AD的取值范围,【感知方法】他思索了很久,但没有思路.老师提示他要添加适当的辅助线,如图②.
方法一:延长AD至点E , 使得 , 连接CE;
方法二:过点C作 , 交AD的延长线于点E . 添加辅助线后,小明恍然大悟,易得 , 再利用三角形的三边关系就可以解决问题.
 (1)、在老师的提示下,小明求得AD长度的范围是大于且小于;(2)、【知识迁移】如图③,已知和为两个等腰直角三角形,其中 , , , F为CD的中点,请根据上述条件,回答以下问题:
(1)、在老师的提示下,小明求得AD长度的范围是大于且小于;(2)、【知识迁移】如图③,已知和为两个等腰直角三角形,其中 , , , F为CD的中点,请根据上述条件,回答以下问题:① ▲ ;
②试探究线段AF与BE的数量关系,并写出解答过程,
(3)、【结论应用】在(2)的条件下,若 , , , 四边形BCDE的面积为 , 则点D到线段AF的距离为(直接写出答案,不需要解答过程).五、综合题
-
18. 已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
 (1)、直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)、直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.19.
(1)、直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)、直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.19. (1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.