【基础版】浙教版数学八上1.5三角形全等的判定同步练习

试卷更新日期：2024-08-01 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为（　　）

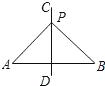A、6 B、5 C、4 D、3

查看试题解析
2. 如图所示，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
3. 如图，已知AC⊥BD，垂足为O，AO＝CO，AB＝CD，则可得到△AOB≌△COD，理由是（）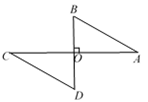

A、HL B、SAS C、ASA D、SSS

查看试题解析
4. 如图，已知 $A C = A D$ ，再添加一个条件仍不能判定 $Δ A B C ≅ Δ A B D$ 的是（）

A、 $∠ C = ∠ D = 90 °$ B、 $∠ B A C = ∠ B A D$ C、 $B C = B D$ D、 $∠ A B C = ∠ A B D$

查看试题解析
5. 如图，O为AC的中点，若要利用“SAS”来判定△AOB≌△COD，则应补充的一个条件是（）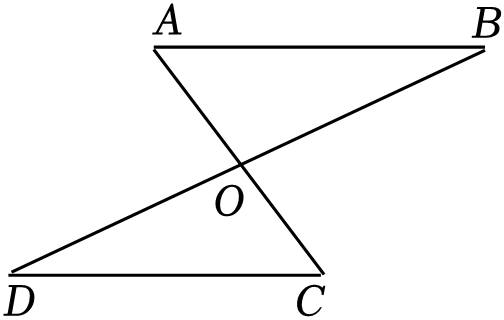

A、∠A＝∠C B、AB＝CD C、∠B＝∠C D、OB＝OD

查看试题解析
6. 如图，小筧家里有一块三角形玻璃碎了，他带着残缺的玻璃去玻璃店配一块与原来相同的，请问师傅配出相同玻璃的依据是（）

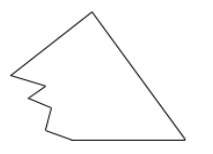A、SSS B、SAS C、AAS D、ASA

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ B A C$ 的角平分线，若 $B C = 5 c m$ ， $B D = 3 c m$ ，则点 $D$ 到 $A B$ 的距离为（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，用螺丝钉将两根小棒 $A D ， B C$ 的中点固定，利用全等三角形知识，测得 $C D$ 的长就是锥形瓶内径 $A B$ 的长，其中，判定 $△ A O B$ 和 $△ D O C$ 全等的方法是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析

二、填空题

9. 如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结AD，CD．则△ABC≌△ADC的依据是．

查看试题解析
10. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是．

查看试题解析
11. 如图，已知线段 $A B$ ，分别以点 $A, B$ 为圆心，5为半径作弧相交于点 $C, D$ ．连接 $C D$ ，点E在 $C D$ 上，连接 $C A, C B, E A, E B$ ．若 $△ A B C$ 与 $△ A B E$ 的周长之差为4，则 $A E$ 的长为．

查看试题解析
12. 已知 $△ A B C$ ， $∠ A = 80 °$ ， $∠ A B C$ 和 $∠ A C B$ 的平分线交于点O，过点O作BC的平行线分别交AB，AC于点E，F．则 $∠ E O B$ 与 $∠ C O F$ 的度数和为．

查看试题解析

三、作图题

13. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ．

(1)、作 $∠ A B C$ 的平分线 $B D$ ，交 $A C$ 于点 $D$ ；（尺规作图，保留作图痕迹，不写作法）

(2)、在（1）的条件下：
①若 $∠ A = 38 °$ ．求 $∠ A D B$ 的度数；
②若 $A B = 5, C D = 2$ ，求 $△ A B D$ 的面积．

查看试题解析

四、解答题

14. 某段河流的两岸是平行的，某数学兴趣小组在老师的带领下不用涉水过河就能测得河的宽度，他们是这样做的：
①在河流的岸边点B处，选对岸正对的一棵树A；
②沿河岸直行 $15 m$ 处有一棵树C ，继续前行 $15 m$ 到达点D处；
③从点D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的点E处时，停止行走；
④测得DE的长为 $10 m$

(1)、请你判断他们做法的正确性并说明理由；

(2)、河的宽度是多少米？

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B$ 的垂直平分线分别交 $A B$ ， $B C$ 于点D ， E ， $A C$ 的垂直平分线分别交 $A C$ ， $B C$ 于点F ， G ，连接 $A E$ ， $A G$ .若 $△ A E G$ 的周长为10，求线段 $B C$ 的长.

查看试题解析
16. 已知：如图， $A C$ 与 $D B$ 相交于点 $O$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ，求证： $A B = D C$ ．

查看试题解析
17. 在 $R t △ A B C$ 中， $∠ B A C = 90 ° ， A B = A C$ ，过直角顶点 $A$ 作直线 $M N ， B D ⊥ M N$ 于点 $D ， C E ⊥ M N$ 于点 $E$ ．

(1)、如图1，当 $M N$ 与 $B C$ 边不相交时，判断 $B D ， C E ， D E$ 之间的数量关系，并说明理由；

(2)、当 $M N$ 与边 $B C$ 相交时，请在图2中画出图形，并直接写出 $B D ， C E ， D E$ 之间的数量关系．

查看试题解析

【基础版】浙教版数学八上1.5三角形全等的判定 同步练习

一、选择题

二、填空题

三、作图题

四、解答题

【基础版】浙教版数学八上1.5三角形全等的判定同步练习