【提升版】浙教版数学八上1.4全等三角形 同步练习
试卷更新日期:2024-07-31 类型:同步测试
一、选择题
-
1. 在下列各组图形中,属于全等图形的是( )A、

 B、
B、
 C、
C、
 D、
D、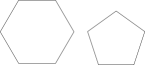 2. 已知下图中的两个三角形全等,则∠1 的度数是( )
2. 已知下图中的两个三角形全等,则∠1 的度数是( ) A、76° B、50° C、54 D、60°3. 如图,△ABC≌△AED , 点E在线段BC上,∠1=40°,则∠AED的度数是( )
A、76° B、50° C、54 D、60°3. 如图,△ABC≌△AED , 点E在线段BC上,∠1=40°,则∠AED的度数是( )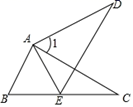 A、70° B、68° C、65° D、60°4. 如图,将直角沿方向平移得到直角 , 已知 , , , 则阴影部分的面积为( )
A、70° B、68° C、65° D、60°4. 如图,将直角沿方向平移得到直角 , 已知 , , , 则阴影部分的面积为( ) A、36 B、37 C、38 D、395. 如图 , 在矩形 中, , 延长 至点 , 使 , 连结 , 动点 从点 出发, 以每秒 2 个单位的速度沿 向终点 运动. 设点 的运动时间为 , 要使 和 全等,则 的值为( )
A、36 B、37 C、38 D、395. 如图 , 在矩形 中, , 延长 至点 , 使 , 连结 , 动点 从点 出发, 以每秒 2 个单位的速度沿 向终点 运动. 设点 的运动时间为 , 要使 和 全等,则 的值为( ) A、1 B、1 或 3 C、1 或 7 D、3 或 76. 如图,将周长为的沿边向右移动 , 得到 , 则四边形的周长是( ) .
A、1 B、1 或 3 C、1 或 7 D、3 或 76. 如图,将周长为的沿边向右移动 , 得到 , 则四边形的周长是( ) . A、17 B、19 C、22 D、247. 如图所示,△ABC≌△BAD,点A与点B,点C与点D是对应顶点,如果∠DAB=50°,∠DBA=40°,那么∠DAC的度数为( )
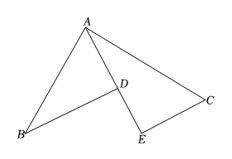
A、17 B、19 C、22 D、247. 如图所示,△ABC≌△BAD,点A与点B,点C与点D是对应顶点,如果∠DAB=50°,∠DBA=40°,那么∠DAC的度数为( ) A、50° B、40° C、10° D、5°8. 如图,已知点D在AC上,点B在AE上, , 且∠BDA=∠A,若∠A:∠C=4:3.则∠DBC=( )
A、50° B、40° C、10° D、5°8. 如图,已知点D在AC上,点B在AE上, , 且∠BDA=∠A,若∠A:∠C=4:3.则∠DBC=( ) A、12° B、24° C、20° D、36°
A、12° B、24° C、20° D、36°二、填空题
-
9. 如图, , , , 点E在BC上,则CE的长度为 .
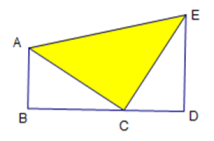
 10. 如图,把梯形沿方向平移得到梯形 , 其中 , , , , 则阴影部分面积为 .
10. 如图,把梯形沿方向平移得到梯形 , 其中 , , , , 则阴影部分面积为 . 11. 如图, , , , 则的度数为 .
11. 如图, , , , 则的度数为 . 12. 如图, , , , 此时点恰好在线段上,则的度数为 .
12. 如图, , , , 此时点恰好在线段上,则的度数为 .
三、作图题
-
13. 如图,矩形纸片的长为4,宽为3,矩形内已用虚线画出网格线,每个小正方形的边长均为1,小正方形的顶点称为格点,现沿着网格线对矩形纸片进行剪裁,使其分成两块纸片.请在下列备用图中,用实线画出符合相应要求的剪裁线.
注:①剪裁过程中,在格点处剪裁方向可发生改变但仍须沿着网格线剪裁;
②在各种新法中,若剪裁线通过旋转、平移或翻折后能完全重合则视为同一情况.

四、解答题
-
14. 如图所示,在正方形中, , 是上的一点且 , 连接 , 动点从点以每秒个单位长度的速度沿向终点运动,设点的运动时间为秒,当和全等时,求的值.
 15. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上.
15. 如图,△ABD≌△CAE,点A,D,E三点在一条直线上. (1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.16. 如图,已知△ABC≌△DEF , 点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)、求证:BD=CE+DE;(2)、当△ABD满足什么条件时,BD∥CE? 请说明理由.16. 如图,已知△ABC≌△DEF , 点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2. (1)、求∠F的度数与DH的长;(2)、求证: .
(1)、求∠F的度数与DH的长;(2)、求证: .五、综合题
-