【培优版】浙教版数学八上1.3证明同步练习-在线组卷题库

1. 定理：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．

已知：如图，直线 $m$ ， $n$ 被直线 $l$ 所截， $∠ 1 = ∠ 2$ ．

对 $m / / n$ 说明理由．

方法 $1$ ：

如图， $∵ ∠ 1 = ∠ 2 = 62 ° ($ 量角器测量所得 $)$ ，

$∠ 1 = ∠ 3 = 62 ° ($ 对顶角相等 $)$ ，

$∴ ∠ 2 = ∠ 3 ($ 角的度数相等 $)$ ．

$∴ m / / n ($ 同位角相等，两直线平行 $)$ ．

方法 $2$ ：

如图， $∵ ∠ 1 = ∠ 2 ($ 已知 $)$ ，

$∠ 1 = ∠ 3 ($ 对顶角相等 $)$ ，

$∴ ∠ 2 = ∠ 3 ($ 等量代换 $)$ ，

$∴ m / / n ($ 同位角相等，两直线平行 $)$ ．

下列说法正确的是（）

A、方法

1

只要测量够

100

组内错角进行验证，就能说明该定理的正确性 B、方法

1

用特殊到一般的数学方法说明了该定理的正确性 C、方法

2

用严谨的推理说明了该定理的正确性 D、方法

2

还需说明其他位置的内错角，对该定理的说明才完整

查看试题解析

2. 定理：三角形的内角和等于180°．

已知： $△ A B C$ 的三个内角为 $∠ A$ 、 $∠ B$ 、 $∠ C$

求证： $∠ A + ∠ B + ∠ C = 180 °$ ．

证法1：如图

∵ $∠ A = 100 °$ ， $∠ B = 30 °$ ， $∠ C = 50 °$ （量角器测量）

∵ $100 ° + 30 ° + 50 ° = 180 °$ （计算所得）

∴ $∠ A + ∠ B + ∠ C = 180 °$ （等量代换）

证法2：如图，延长 $B C$ 到 $D$ ，过点 $C$ 作 $C E / / A B$ ．

∴ $∠ A = ∠ 2$ （两直线平行，内错角相等）

$∠ B = ∠ 3$ （两直线平行，同位角相等）

∵ $∠ 1 + ∠ 2 + ∠ 3 = 180 °$ （平角定义）．

∴ $∠ 1 + ∠ A + ∠ B = 180 °$ （等量代换）

即 $∠ A + ∠ B + ∠ C = 180 °$ ．

下列说法正确的是（）

A、证法1采用了从特殊到一般的方法证明了该定理 B、证法1还需要测量一百个进行验证，就能证明该定理 C、证法2还需证明其它形状的三角形，该定理的证明过程才完整 D、证法2用严谨的推理证明了该定理

查看试题解析

3. 在下面的括号内填上推理的依据．
如图， $A C$ 和 $B D$ 相交于点 $O$ ， $∠ B ＝ ∠ D$ ．

证明： $∵ ∠ B ＝ ∠ D$ （已知），
$∴ A B ∥ C D$ ，；
∴ $∠ A ＝ ∠ C$ ．

查看试题解析
4. 完成下面的证明：

(1)、已知：如图，AB∥CD
求证：∠1+∠3 = 180°

证明：∵ AB∥CD（已知），

∴ ∠1+∠2 = 180°（）

又∵ ∠2 = ∠3（）

∴ ∠1+∠3=180°（）

(2)、已知：如图，AM∥EF ， ∠1 = ∠B ．
求证：∠2 = ∠C ．

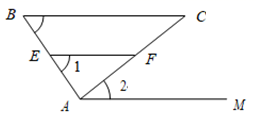
证明：∵ ∠1 = ∠B（已知），

∴ EF∥BC（）

∵ AM∥EF（已知），

∴ AM∥BC（）

∴ ∠2 = ∠C（）

查看试题解析

5.

(1)、如图 1， $E D ∥ B A ， ∠ E = ∠ B$ ．说明 $B C ∥ E F$ 的理由．

(2)、如图 2， $E D ∥ B A ， ∠ B + ∠ E = 180^{\circ}$ ．判断直线 $B C$ 与直线 $E F$ 的位置关系，并说明理由．

(3)、根据以上探究，你发现了一个什么结论？请你写出来．

查看试题解析
6. 如图，已知 $A D ∥ B C$ ， $∠ A = ∠ C$

(1)、如图1，试说明： $A B ∥ C D$ ；

(2)、如图2，连接 $B D$ ，若点E ， F在线段 $A B$ 上，且满足 $D B$ 平分 $∠ F D C$ ， $D E$ 平分 $∠ A D F$ ， $∠ A = ∠ C = 110 °$ ，求 $∠ E D B$ 的度数；

(3)、下列①-③的问题，对应分值分别为4分、5分、6分，请根据你的认知水平，选择其中一个问题作答，解答对多个问题，按分值最高的一个问题记分．
①如图2，在（2）的条件下，若 $∠ A = ∠ C = x °$ ，求 $∠ E D B$ 的度数；（用含x的代数式表示）．
②如图3，在（2）的条件下，将线段 $B C$ 沿着射线 $A B$ 的方向向右平移，当 $D F$ 平分 $∠ E D B$ 时，若 $∠ A = ∠ C = x °$ ，求 $∠ A E D$ 的度数；（用含x的代数式表示）
③如图3，在（2）的条件下，将线段 $B C$ 沿着射线 $A B$ 的方向向右平移，当 $∠ A E D = ∠ C B D$ 时，若 $∠ A = ∠ C = x °$ ，求 $∠ A B D$ 的度数．（用含x的代数式表示）．

查看试题解析
7. 已知有限张卡片，每张卡片上各写有一个小于30的正数，所有卡片上数的和为1080．现将这些卡片按下列要求一批一批地取走（不放回）直至取完．首先从这些卡片中取出第一批卡片，其数字之和为S₁ ，满足S₁≤120，且S₁要尽可能地大；然后在取出第一批卡片后，对余下的卡片按第一批的取卡要求构成第二批卡片（其数字之和为S₂）；如此继续构成第三批（其数字之和为S₃）；第四批（其数字之和为S₄）；…直到第N批（其数字之和为S_N）取完所有卡片为止．
（1）判断S₁ ， S₂ ， …，S_N的大小关系，并指出除第N批外，每批至少取走的卡片数为多少？
（2）当n=1，2，3，…，N﹣2时，求证： S_n< $\frac{960}{n}$ ；
（3）对于任意满足条件的有限张卡片，证明：N≤11．

查看试题解析

8.
【问题背景】如图， $∠ A O B = α (0 ° < α < 90 °)$ ，一块三角板 $C D E$ 中， $∠ C E D = 90 °$ ， $∠ C D E = 30 °$ ，将三角板 $C D E$ 如图所示放置，使顶点C落在 $O B$ 边上，经过点D作直线 $M N ∥ O B$ 交 $O A$ 边于点M ，且点M在点D的左侧．

(1)、【问题解决】如图1，过点E作 $E F ∥ M N$ ，若 $C E ∥ O A$ ， $∠ N D E = 45 °$ ，则 $α =$ °；

(2)、若 $∠ M D C$ 的平分线 $D F$ 交 $O B$ 边于点F ．
【探索求证】①如图2，当 $D F ∥ O A$ ，且 $α = 60 °$ 时，试说明： $C E ∥ O A$ ；
【延伸扩展】②如图3，当 $C E ∥ O A$ 保持不变时，试求出 $∠ O F D$ 与 $α$ 之间的数量关系．

查看试题解析
9. 【学科融合】
物理学光的反射现象中，反射光线、入射光线和法线都在同一个平面内，反射光线和入射光线分别位于法线两侧，反射角等于入射角，这就是光的反射定律．

(1)、【理解运用】
如图1，展示了光线反射定律，EF是镜面AB的垂线，一束光线m射到平面镜AB上，被AB反射后的光线为n ，则入射光线m ，反射光线n与垂线EF所夹的锐角 $θ_{1} = θ_{2}$ ，则 $∠ 1$ $∠ 2$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）；

(2)、【尝试探究】
学完光的反射定律，数学兴趣小组的同学想利用这个定律结合数学知识制作一个简易潜望镜，并画出了潜望镜的工作原理示意图，如图2，AB、CD是平行放置的两面平面镜，入射光线EF经过两次反射后，得到的反射光线GH ，已知 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．请问进入潜望镜的光线EF和离开潜望镜的光线GH是否平行，说明理由．

(3)、【拓展应用】
如图3，AB、BC是两平面镜，入射光线FE经过两次反射后，反射光线GH与入射光线EF平行但方向相反．已知 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．求 $∠ 2 + ∠ 3$ 的度数．

查看试题解析

【培优版】浙教版数学八上1.3证明同步练习

一、选择题

二、填空题

三、解答题

四、实践探究题

【培优版】浙教版数学八上1.3证明 同步练习

一、选择题

二、填空题

三、解答题

四、实践探究题

【培优版】浙教版数学八上1.3证明同步练习