【培优版】浙教版数学八上1.1认识三角形 同步练习
试卷更新日期:2024-07-31 类型:同步测试
一、选择题
-
1. 下列各组数分别表示三条线段的长度,其中能构成三角形的是( )A、5cm,8cm,3cm B、10cm,5cm,8cm C、12cm,5cm,6cm D、6cm,6cm,12cm2. 如图,在中, , AE平分 , 若 , , 则的度数是( )
 A、10° B、12° C、13° D、15°3. 如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( )
A、10° B、12° C、13° D、15°3. 如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( ) A、15 B、17 C、20 D、224. 如图,将直角三角板放置在矩形纸片上,若 , 则的度数为( )
A、15 B、17 C、20 D、224. 如图,将直角三角板放置在矩形纸片上,若 , 则的度数为( ) A、55° B、45° C、35° D、30°5. 如图,点P是△ABC的AB边上一动点,当S△APC=S△BPC时,则CP是△ABC的( )
A、55° B、45° C、35° D、30°5. 如图,点P是△ABC的AB边上一动点,当S△APC=S△BPC时,则CP是△ABC的( ) A、高 B、中线 C、角平分线 D、中位线6. 如图所示,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是( )
A、高 B、中线 C、角平分线 D、中位线6. 如图所示,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是( ) A、BF=CF B、∠C+∠CAD=90° C、∠BAF=∠CAF D、S△ABC=2S△ABF7. 如图,在平面直角坐标系中,点A , B , C的坐标分别为 , , 连接 , , 若 . 点M是直线上的一个动点,当最短时,求( )
A、BF=CF B、∠C+∠CAD=90° C、∠BAF=∠CAF D、S△ABC=2S△ABF7. 如图,在平面直角坐标系中,点A , B , C的坐标分别为 , , 连接 , , 若 . 点M是直线上的一个动点,当最短时,求( ) A、5 B、 C、 D、38. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A、5 B、 C、 D、38. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )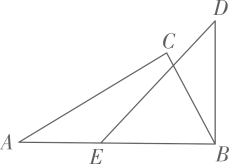 A、或或 B、或或 C、或或 D、或或
A、或或 B、或或 C、或或 D、或或二、填空题
-
9. 如图,在中,和的平分线相交于点P , 若 , 则的度数为 .
 10. 如图,将平移到的位置(点在边上),若 , , 则的度数为 .
10. 如图,将平移到的位置(点在边上),若 , , 则的度数为 . 11. 如图,△ABC中,D是AB的中点,且 , , 则.
11. 如图,△ABC中,D是AB的中点,且 , , 则. 12. 如图,直角三角形中, , , , , 点D是边上一动点,作直线经过点C、点D , 分别过点A , B作与垂直,与垂直,垂足分别为点F , E . 设线段 , 的长度分别为 , , 则的最大值为 .
12. 如图,直角三角形中, , , , , 点D是边上一动点,作直线经过点C、点D , 分别过点A , B作与垂直,与垂直,垂足分别为点F , E . 设线段 , 的长度分别为 , , 则的最大值为 .
三、作图题
-
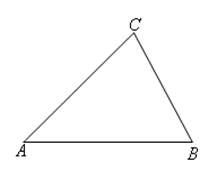
13. 已知: 如图△ABC,
求作: 一点P, 使P在BC上, 且点P到∠BAC的两边的距离相等.
(要求尺规作图, 并保留作图痕迹, 不要求写作法)
 14. 在中,AD是的平分线,其中点在边BC上.
14. 在中,AD是的平分线,其中点在边BC上. (1)、用圆规和直尺在图中作出角平分线AD.(不要求写作法,保留作图痕迹)(2)、若 , , 求的度数.
(1)、用圆规和直尺在图中作出角平分线AD.(不要求写作法,保留作图痕迹)(2)、若 , , 求的度数.四、解答题
-
15. 如图,在三角形内部有一点F , 点D , E分别是边上的点, , .
 (1)、判断与是否平行,并说明理由.(2)、若平分 , , 求的度数.
(1)、判断与是否平行,并说明理由.(2)、若平分 , , 求的度数.五、实践探究题
-
16. 阅读材料:如果一个三角形的三边长分别为 , 记 , 那么这个三角形的面积为 . 这个公式叫“海伦公式”,它是利用三角形的三条边的边长直接求三角形面积的公式,中国秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦—秦九韶公式”.完成下列问题:

如图,在中, .
(1)、求的面积;(2)、过点作 , 垂足为 , 求线段的长.六、综合题
-

