浙教版数学九上章末重难点专训 简单事件的概率-转盘问题
试卷更新日期:2024-07-31 类型:单元试卷
一、选择题
-
1. 如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( )
 A、1号 B、2号 C、3号 D、4号2. 如图,转盘中6个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针所指的数是质数的概率为( )
A、1号 B、2号 C、3号 D、4号2. 如图,转盘中6个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针所指的数是质数的概率为( ) A、 B、 C、 D、3. 某商场为吸引顾客,设计了如图所示的自由转盘,当指针指向阴影部分时,该顾客可获得奖品一份,那么该顾客获奖的概率为( )
A、 B、 C、 D、3. 某商场为吸引顾客,设计了如图所示的自由转盘,当指针指向阴影部分时,该顾客可获得奖品一份,那么该顾客获奖的概率为( ) A、 B、 C、 D、4. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、
A、 B、 C、 D、4. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、 B、
B、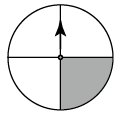 C、
C、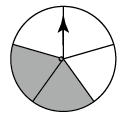 D、
D、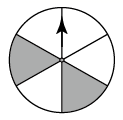 5. 如图,转盘中8个扇形的面积都相等,涂色的为灰色部分,其余为白色部分,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( )
5. 如图,转盘中8个扇形的面积都相等,涂色的为灰色部分,其余为白色部分,任意转动这个转盘1次,当转盘停止转动时,指针落在灰色区域的概率是( ) A、 B、 C、 D、6. 五一期间,某商场设计了一个“玩转盘,享优惠”活动:如图所示的转盘盘面被分成四个相等的扇形区域,并分别标有文字满江红、红旗渠、殷墟、大峡谷.若转动转盘两次,每次转盘停止后指针所指区域都是“满江红”,将获得一张优惠券(当指针恰好指在分界线上时重转).小王转动转盘两次,获得优惠券的概率为( )
A、 B、 C、 D、6. 五一期间,某商场设计了一个“玩转盘,享优惠”活动:如图所示的转盘盘面被分成四个相等的扇形区域,并分别标有文字满江红、红旗渠、殷墟、大峡谷.若转动转盘两次,每次转盘停止后指针所指区域都是“满江红”,将获得一张优惠券(当指针恰好指在分界线上时重转).小王转动转盘两次,获得优惠券的概率为( ) A、 B、 C、 D、7. 如图,将转盘八等分,分别涂上红、绿、蓝三种颜色,则转动的转盘停止时.指针落在蓝色区域的概率为( )
A、 B、 C、 D、7. 如图,将转盘八等分,分别涂上红、绿、蓝三种颜色,则转动的转盘停止时.指针落在蓝色区域的概率为( ) A、 B、 C、 D、8. 如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A、 B、 C、 D、8. 如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 某试验小组做了可转动转盘(如图),想求当转盘停止转动后,“指针落在灰色区域内”的概率,试验数据如下表:
试验次数n
20
40
60
80
100
1000
“指针落在灰色区域内”的次数m
6
11
15
21
25
251
“指针落在灰色区域内”的频率
0.3
0.275
0.25
0.2625
0.25
0.251
根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率约是 . (结果精确到0.01)
 10. 如图,是一个材质均匀的转盘,转盘分成8个全等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止(若指针指向两个扇形的交线时,当作指向右边的扇形),转动一次转盘,转盘停止后指针指向红色扇形的概率是 .
10. 如图,是一个材质均匀的转盘,转盘分成8个全等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止(若指针指向两个扇形的交线时,当作指向右边的扇形),转动一次转盘,转盘停止后指针指向红色扇形的概率是 .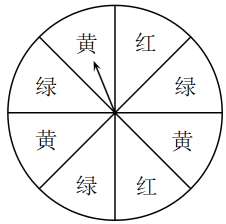 11. 如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点落在直角坐标系第二象限的概率是 .
11. 如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点落在直角坐标系第二象限的概率是 .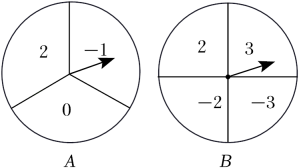 12. 如图,转盘被分成5个面积相等的扇形,任意转动这个转盘1次,当转盘停止转动时,指针落在阴影区域的概率为 .
12. 如图,转盘被分成5个面积相等的扇形,任意转动这个转盘1次,当转盘停止转动时,指针落在阴影区域的概率为 . 13. 如图是一个游观转盘,自由转动转盘,当转盘停止转动后,指针落在色区域的概率最大
13. 如图是一个游观转盘,自由转动转盘,当转盘停止转动后,指针落在色区域的概率最大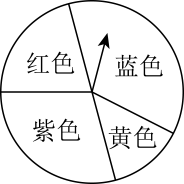 14. 如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,且分别标有数字,分别转动两个转盘一次,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),则两个指针所指区域的数字之积为偶数的概率是 .
14. 如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,且分别标有数字,分别转动两个转盘一次,转盘停止时(若指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止),则两个指针所指区域的数字之积为偶数的概率是 .
三、解答题
-
15. 如图,三个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色小强和小亮用转盘和转盘做一个转盘游戏:同时转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则小强获胜;若两个转盘转出的颜色相同,则小亮获胜;在其他情况下,小强和小亮不分胜负.
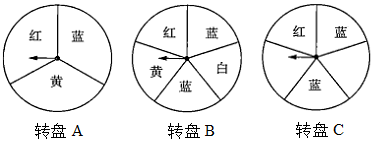 (1)、用画树状图或列表的方法表示此游戏所有可能出现的结果;(2)、小强说,此游戏不公平请你说明理由;(3)、请你在转盘的空白处,涂上适当颜色,使得用转盘替换转盘后,使游戏对小强和小亮是公平的(在空白处填写表示颜色的文字即可,不要求说明理由,只需给出一种结果即可).16. 如图,甲、乙是两个可以自由转动的转盘,转盘均被分成三个面积相等的扇形,每个扇形中都标有相应的数字,指针的位置固定.同时转动两个转盘,请利用画树状图或列表的方法求甲、乙转盘停止后指针所指向的数字之和为奇数的概率.(当指针指在边界线上时视为无效,需重新转动转盘)
(1)、用画树状图或列表的方法表示此游戏所有可能出现的结果;(2)、小强说,此游戏不公平请你说明理由;(3)、请你在转盘的空白处,涂上适当颜色,使得用转盘替换转盘后,使游戏对小强和小亮是公平的(在空白处填写表示颜色的文字即可,不要求说明理由,只需给出一种结果即可).16. 如图,甲、乙是两个可以自由转动的转盘,转盘均被分成三个面积相等的扇形,每个扇形中都标有相应的数字,指针的位置固定.同时转动两个转盘,请利用画树状图或列表的方法求甲、乙转盘停止后指针所指向的数字之和为奇数的概率.(当指针指在边界线上时视为无效,需重新转动转盘) 17. 如图,两个相同的可以自由转动的转盘A和B , 转盘A被三等分,分别标有数字6,2,1;转盘B被四等分,分别标有数字 , , , .(当指针指在两个扇形的交线时,需重新转动转盘)
17. 如图,两个相同的可以自由转动的转盘A和B , 转盘A被三等分,分别标有数字6,2,1;转盘B被四等分,分别标有数字 , , , .(当指针指在两个扇形的交线时,需重新转动转盘) (1)、转动转盘B一次,转盘停止时,指针指向偶数的概率为;(2)、同时转动两个转盘,转盘停止时,求两个指针指向的数字之和大于0的概率.(画树状图或列表法)18. 某商场为吸引消费者,举行幸运大转盘活动,规定顾客消费满100元就可获得转如图所示的转盘(转盘被平均分成3份)的机会.为了活跃气氛,该商场设计了两个方案:
(1)、转动转盘B一次,转盘停止时,指针指向偶数的概率为;(2)、同时转动两个转盘,转盘停止时,求两个指针指向的数字之和大于0的概率.(画树状图或列表法)18. 某商场为吸引消费者,举行幸运大转盘活动,规定顾客消费满100元就可获得转如图所示的转盘(转盘被平均分成3份)的机会.为了活跃气氛,该商场设计了两个方案:方案一:转动转盘一次,若指针指向数字1可领取一份奖品;
方案二:转动转盘两次,若两次指针指向的数字之和为奇数可领取一份奖品.(若指针指向分界线,则重转)
 (1)、若转动转盘一次,则领取到一份奖品的概率为;(2)、若转动转盘两次,用树状图列举出所有等可能出现的结果;(3)、如果你获得转动转盘的机会,想要领取到奖品,你会选择哪个方案?并说明理由.19. 如图,有甲、乙两个完全相同的转盘均被分成A,B两个区域,甲转盘中A区域的圆心角是120°,乙转盘中A区域的圆心角是90°,自由转动转盘(如果指针指向区域分界线则重新转动).
(1)、若转动转盘一次,则领取到一份奖品的概率为;(2)、若转动转盘两次,用树状图列举出所有等可能出现的结果;(3)、如果你获得转动转盘的机会,想要领取到奖品,你会选择哪个方案?并说明理由.19. 如图,有甲、乙两个完全相同的转盘均被分成A,B两个区域,甲转盘中A区域的圆心角是120°,乙转盘中A区域的圆心角是90°,自由转动转盘(如果指针指向区域分界线则重新转动). (1)、转动甲转盘一次,求指针指向A区域的概率.(2)、自由转动两个转盘各一次,利用树状图或列表法,求两个转盘指针同时指向B区域的概率.20. 小明与小红在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动转盘停止后,指针必须指到某一数字,否则重转.
(1)、转动甲转盘一次,求指针指向A区域的概率.(2)、自由转动两个转盘各一次,利用树状图或列表法,求两个转盘指针同时指向B区域的概率.20. 小明与小红在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动转盘停止后,指针必须指到某一数字,否则重转. (1)、小明转动转盘B , 转到的数字是偶数的概率为:;(2)、现游戏规则为:转盘A转出的数字记为x , 转盘B转出的数字记为y , 若x , y满足xy>6,则小明胜,若xy<6,则小红胜,请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.21. 如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其他完全相同),转盘甲上的数字分别是-6,-1,8,转盘乙上的数字分别是-4,5,7(规定:指针恰好停留在分界线上,则重新转一次).
(1)、小明转动转盘B , 转到的数字是偶数的概率为:;(2)、现游戏规则为:转盘A转出的数字记为x , 转盘B转出的数字记为y , 若x , y满足xy>6,则小明胜,若xy<6,则小红胜,请用列表法或画树状图的方法说明这个游戏规则对双方是否公平.21. 如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其他完全相同),转盘甲上的数字分别是-6,-1,8,转盘乙上的数字分别是-4,5,7(规定:指针恰好停留在分界线上,则重新转一次). (1)、转动转盘,转盘甲指针指向正数的概率是;转盘乙指针指向正数的概率是.(2)、若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表或画树状图的方法求满足a+b<0的概率.22. 小明和小亮用如图所示的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由.若不公平,请你修改规则使游戏对双方公平.
(1)、转动转盘,转盘甲指针指向正数的概率是;转盘乙指针指向正数的概率是.(2)、若同时转动两个转盘,转盘甲指针所指的数字记为a,转盘乙指针所指的数字记为b,请用列表或画树状图的方法求满足a+b<0的概率.22. 小明和小亮用如图所示的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由.若不公平,请你修改规则使游戏对双方公平. 23. 平遥古城和云冈石窟是山西省著名的两个景区,甲、乙两人想用做游戏的方式决定去哪一个景区.他们准备了两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,同时转动两个转盘,若两个指针指向的数字之积小于3,则去平遥古城,否则去云冈石窟,若指针刚好落在分割线上,则需要重新转动转盘,请用列表或画树状图的方法说明这个游戏是否公平.
23. 平遥古城和云冈石窟是山西省著名的两个景区,甲、乙两人想用做游戏的方式决定去哪一个景区.他们准备了两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,同时转动两个转盘,若两个指针指向的数字之积小于3,则去平遥古城,否则去云冈石窟,若指针刚好落在分割线上,则需要重新转动转盘,请用列表或画树状图的方法说明这个游戏是否公平. 24. 如图(1)所示的是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指位置(指针指向两扇形的交线时,当作指向右边的扇形).如图(2)所示的是一个不透明的口袋.其中装有3个完全相同的小球,分别标着数字-1,2,3.
24. 如图(1)所示的是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指位置(指针指向两扇形的交线时,当作指向右边的扇形).如图(2)所示的是一个不透明的口袋.其中装有3个完全相同的小球,分别标着数字-1,2,3. (1)、请你在转盘的四个扇形中分别填入一个适当的实数,使得转动的转盘停止后,指针指向负数的概率为;(2)、在(1)的情况下,转动的转盘停止后,指针指向的数记为m;从口袋中随机摸出一个小球,将标着的数记为n.求点(m,n)落在第四象限的概率.25. 为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平.
(1)、请你在转盘的四个扇形中分别填入一个适当的实数,使得转动的转盘停止后,指针指向负数的概率为;(2)、在(1)的情况下,转动的转盘停止后,指针指向的数记为m;从口袋中随机摸出一个小球,将标着的数记为n.求点(m,n)落在第四象限的概率.25. 为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平. 26. 如图是两个转盘,每个转盘都被圆的半径三等分,甲转盘的三个扇形上标有数字2,4,6,乙转盘的三个扇形上标有数字1,3,5,小明和小力分别转动甲、乙转盘,每入转动一次,记录转盘停止后指针指向的数字,若指针指在分界线上则重转.
26. 如图是两个转盘,每个转盘都被圆的半径三等分,甲转盘的三个扇形上标有数字2,4,6,乙转盘的三个扇形上标有数字1,3,5,小明和小力分别转动甲、乙转盘,每入转动一次,记录转盘停止后指针指向的数字,若指针指在分界线上则重转. (1)、两人分别转动甲、乙转盘后,可能出现的全部可能有哪些?请用列表或画树状图的方法表示.(2)、若得到的两数字之和是3的倍数,则小明赢;若得到的两数字之和是7的倍数,则小力赢,此游戏公平吗?为什么?
(1)、两人分别转动甲、乙转盘后,可能出现的全部可能有哪些?请用列表或画树状图的方法表示.(2)、若得到的两数字之和是3的倍数,则小明赢;若得到的两数字之和是7的倍数,则小力赢,此游戏公平吗?为什么?