浙教版数学九上第2章 简单事件的概率 三阶单元测试卷

试卷更新日期：2024-07-31 类型：单元试卷

进入 出卷网 下载

一、选择题（本题有10小题，每小题3分，共30分）

  • 1.  一个不透明的袋子中只装有红球和黄球，这些球除颜色外都相同．将袋子中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回袋子中．不断重复这一过程，摸出1000次球，发现有800次摸到红球．从口袋中随机摸一次，摸到红球的概率大约为（    ）
    A、0.2 B、0.4 C、0.6 D、0.8

    查看试题解析

  • 2. 下列说法正确的是（　　）
    A、“经过有交通信号的路口遇到红灯”是必然事件         B、已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次 C、投掷一枚硬币正面朝上是随机事件 D、明天太阳从东方升起是随机事件

    查看试题解析

  • 3. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球，则两次摸出的小球的标号之和等于6的概率是（       ）
    A、13 B、14 C、15 D、316

    查看试题解析

  • 4. 在一个不透明的袋子里装有若干个形状和大小均相同的红、绿、白三种颜色的小球，现从袋中任意摸出一个球，其中摸出白色小球的概率为35 ， 摸出绿色小球的概率为110 ， 已知红色小球的个数为3，那么袋子里共有小球（   ）
    A、6个 B、8个 C、10个 D、12个

    查看试题解析

  • 5. 在一个不透明的箱子里装有m个球，其中红球4个，这些球除颜色外都相同，每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验后发现，摸到红球的频率在0.2，那么可以估算出m的值为（   ）
    A、8 B、12 C、16 D、20

    查看试题解析

  • 6. 端午节，妈妈给小慧准备了4个粽子，其中豆沙粽、蛋黄粽各1个，肉粽2个．小慧从中任取1个粽子，是豆沙粽的概率为（     ）
    A、14 B、13 C、12 D、23

    查看试题解析

  • 7. 如图，一个可以自由转动的转盘，被分成了白色和红色两个区域，任意转动转盘一次，当转盘停止转动时（若指针停在边界处，则重新转动转盘），指针落在红色区域内的概率是（   ）

    A、16 B、15 C、13 D、12

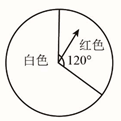    查看试题解析

  • 8. 小江玩投掷飞镖的游戏，他设计了一个下图所示的靶子，点E，F分别是矩形ABCD的两边AD，BC上的点，EF∥AB，点M，N是EF上任意两点，则投一次，飞镖落在阴影部分的概率是（ ）

    A、12 B、13 C、23 D、34

    查看试题解析

  • 9. 甲乙丙丁四人互相给其他三人之一写信，选择对象的方式等可能.问存在两个人收到对方的信的概率（   ）
    A、23 B、59 C、1727 D、5581

    查看试题解析

  • 10. 有2名男生和2名女生，王老师要随机地、两两一对地为他们排座位，一男一女排在一起的概率是（ ）
    A、14 B、13 C、12 D、23

    查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

  • 11. 从 −2 ，0， 2 这三个数中，任取两个不同的数分别作为 a ， b 的值，恰好使得关于 x 的方程 x2+ax−b=0 有实数解的概率为.

    查看试题解析

  • 12. 在如图所示的电路图中，当随机闭合开关A、B、C中的任意一个时，能够使小灯泡发光的概率为 ．

    查看试题解析

  • 13. 某学习小组做“用频率估计概率”的摸球试验：在不透明的盒子中装入红色、蓝色的玻璃球共60个，从中随机摸出一个球，记下颜色后放回，统计了“摸出球为红色”出现的频率，绘制了如图的折线统计图，那么估计盒子中装入红色球的个数约为 ．

    查看试题解析

  • 14. 在一个布袋里装着标号分别为1 ， 2 ， 3的3个小球，它们除标号外无其他区别，从布袋中随机摸出一个小球后不放回，将小球上的数字记为a ， 摇匀再随机摸出一个小球，将小球上的数字记为b ， 则a、b使二次根式a+b的值为有理数的概率是 ．

    查看试题解析

  • 15. 柜子里有5双鞋，取出一只鞋是右脚鞋的概率是 ．

    查看试题解析

  • 16. 取5张看上去无差别的卡片，分别在正面写上数字：−1 ， 1，−2 ， 2，−3 ， 3，现把它们洗匀正面朝下，随机摆放在桌面上.从中任意抽出1张，记卡片上的数字为m ， 则数字m使分式方程x−mx−2+1x=1无解的概率为.

    查看试题解析

三、解答题（本题共8小题，第17题6分，第18题10分，第19题6分，第20题6分，第21题8分，第22题8分，第23题8分，第24题14分，共66分）

  • 17. 某校一年级开设人数相同的A ， B ， C三个班级，甲、乙两位学生是该校一年级新生，开学初学校对所有一年级新生进行电脑随机分班．
    (1)、“学生甲分到A班”的概率是；
    (2)、请用画树状图法或列表法，求甲、乙两位新生分到同一个班的概率．

    查看试题解析

  • 18. 睡眠管理作为“五项管理”中的重要内容之一，也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间，随机抽取该校部分学生进行问卷调查，并将结果进行了统计和整理，绘制成如下统计表和不完整的统计图.

    学生类别

    学生平均每天睡眠时间x(单位：小时)

    A

    7⩽x<7.5

    B

    7.5⩽x<8

    C

    8⩽x<8.5

    D

    8.5⩽x<9

    E

    x⩾9

    (1)、本次抽取调查的学生共有人，扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为.
    (2)、请补全条形统计图．
    (3)、被抽取调查的E类4名学生中有2名女生，2名男生．从这4人中随机抽取2人进行电话回访，请用画树状图或列表的方法，求恰好抽到2名男生的概率.

    查看试题解析

  • 19. 数学文化节猜谜游戏中，有四张大小、形状、质地都相同的字谜卡片，分别记作字谜A、字谜B、字谜C、字谜D ， 其中字谜A、字谜B是猜“数学名词”，字谜C、字谜D是猜“数学家人名”．
    (1)、若小军从中随机抽取一张字谜卡片，则小军抽取的字谜是猜“数学名词”的概率是；
    (2)、若小军一次从中随机抽取两张字谜卡片，请用画树状图或列表的方法求小军抽取的字谜均是猜“数学家人名”的概率．

    查看试题解析

  • 20.  为使学生更加了解云南，热爱家乡，热爱祖国，体验“有一种叫云南的生活”．某校七年级年级组准备从博物馆a、植物园b两个研学基地中，随机选择一个基地研学，且每个基地被选到的可能性相等；八年级年级组准备从博物馆a、植物园b、科技馆c三个研学基地中，随机选择一个基地研学，且每个基地被选到的可能性相等．记选择博物馆a为a ， 选择植物园b为b ， 选择科技馆c为c ， 记七年级年级组的选择为x ， 八年级年级组的选择为y ．
    (1)、请用列表法或画树状图法中的一种方法，求(x,y)所有可能出现的结果总数；
    (2)、求该校七年级年级组、八年级年级组选择的研学基地互不相同的概率P ．

    查看试题解析

  • 21. 某商场进行“6·18”促销活动，设计了如下两种摇奖方式：

    方式一：如图1，有一枚均匀的正二十面体形状的骰子，其中的1个面标有“1”，2个面标有“2”，3个面标有“3”，4个面标有“4”，5个面标有“5”，其余的面标有“6”．将这个骰子掷出后，“6”朝上则获奖；

    方式二：如图2，一个均匀的转盘被等分成12份，分别标有1，2，3，4，5，6，7，8，9，10，11，12这12个数字．转动转盘，当转盘停止后，指针指向的数字为3的倍数则获奖．

    (1)、若采用方式一，骰子掷出后，“5”朝上的概率为；
    (2)、若采用方式二，当转盘停止后，指针指向的数字为“5”的概率为；
    (3)、小明想增加获奖机会，应选择哪种摇奖方式？请通过相关计算，应用概率相关知识说明理由．

    查看试题解析

  • 22. 阅读材料，回答问题：
    (1)、经过某十字路口的汽车，可能直行，也可能向左转或向右转.如果这三种可能性的大小相同，求三辆汽车经过这个十字路口时，至少要两辆车向左转的概率
    (2)、有两把不同的锁和三把钥匙，其中两把钥匙分别能打开这两把锁（一把钥匙只能开一把锁），第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁，一次打开锁的概率是多少？
    (3)、我们可以用“袋中摸球”的试验来模拟题(1)：在口袋中放三个不同颜色的小球，红球表示直行，绿球表示向左转，黑球表示向右转，三辆汽车经过路口，相当于从三个这样的口袋中各随机摸出一球.

    问题：

    ①事件“至少有两辆车向左转”相当于“袋中摸球”的试验中的什么事件？

    ②设计一个“袋中摸球”的试验模拟题2，请简要说明你的方案

    ③请直接写出题2的结果.

    查看试题解析

  • 23. 某学校为落实立德树人根本任务，使每个学生都能得到全面而个性的发展，特举办了“科学竞赛”活动，甲、乙两个班学生的成绩统计如下：

    分数/分

    50

    60

    70

    80

    90

    100

    甲班人数/人

    2

    5

    10

    18

    14

    1

    乙班人数/人

    4

    4

    16

    4

    18

    4

    活动规定：以60分为及格线，并分别设置了一、二、三等奖，100分为一等奖，90分为二等奖，80分为三等奖．小亮分别计算了两个班的平均分和方差，得：x¯甲=78 ， x¯乙=78 ， x¯甲2=128 ， x¯乙2=200 ． 请你根据以上材料回答下列问题．

    (1)、甲、乙两个班的中位数和众数分别是多少？
    (2)、你认为甲、乙两个班哪个班的成绩更优秀？为什么？
    (3)、该校从得100分的两男三女5人中，随机选取2人参加教育局组织的竞赛，请你用列表或画树状图的方法，求出恰好选取一男一女参赛的概率．

    查看试题解析

  • 24. 每年6月26日是“国际禁毒日”．某中学为了让学生掌握禁毒知识，提高防毒意识，组织全校学生参加了“禁毒知识网络答题”活动．该校德育处对八年级全体学生答题成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格；并绘制成如下不完整的统计图．请你根据图1、图2中所给的信息解答下列问题：

     

    (1)、该校八年级共有名学生，“优秀”所占圆心角的度数为 ．
    (2)、请将图1中的条形统计图补充完整．
    (3)、已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动，请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格？
    (4)、德育处从该校八年级答题成绩前四名甲、乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛，请用树状图或列表法求出必有甲同学参加的概率．

    查看试题解析