浙教版数学九上第2章 简单事件的概率 二阶单元测试卷
试卷更新日期：2024-07-31 类型：单元试卷
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 下列说法正确的是（ ）A、调查中央电视台《开学第一课》的收视率，应采用全面调查的方式。 B、数据3，5，4，1，﹣2的中位数是4 C、一个抽奖活动中，中奖概率为 ， 表示抽奖20次就有1次中奖 D、甲、乙两名射击运动员10次射击成绩（单位：环）的平均数相等，方差分别为 ， ， 则甲的成绩比乙的稳定2. “四大古典名著”是中国文学史中的经典作品，是宝贵的世界文化遗产．小沈同学收集到中国古代四大名著卡片，四张卡片除内容外其余完全相同，将这四张卡片背面朝上，洗匀后，从中随机抽取一张（不放回），再从中随机抽取另一张，则抽到的两张卡片恰好是“水浒传”和“西游记”的概率是（ ）
A、 B、 C、 D、3. 某校计划组织研学活动，现有四个地点可供选择：岳麓山、梅溪湖、橘子洲、植物园．若从中随机选择两个地点，则选中“橘子洲”的概率为A、 B、 C、 D、4. 九年一班有12名同学报名参加校园踢毽子比赛，其中8名男生，4名女生，体育委员随机抽出一名同学代表班级参加比赛，则抽出的同学是女生的概率是（ ）A、 B、 C、 D、5. 如图，在正方形中，点M ， N是的三等分点，分别以 ， 为边作正方形．正方形被分为如图所示的三个区域．小明同学在正方形内进行撒豆子试验，以下说法正确的是（ ）
A、豆子落在区域Ⅰ的概率最小 B、豆子落在区域Ⅱ的概率最小 C、豆子落在区域Ⅲ的概率最小 D、豆子落在区域Ⅰ、Ⅱ、Ⅲ的概率相同6. 【背景材料】人的眼皮有单眼皮与双眼皮，这是由对应的基因决定的．研究表明：决定眼皮单双的基因有两种，一种是显性基因（记为B），另一种是隐性基因（记为b）；一个人的基因总是成对出现（如 ， ， ， ），在成对的基因中，一个来自父亲，另一个来自母亲，父母亲提供基因时均为随机的．只要出现了显性基因B，那么这个人就一定是双眼皮。即基因 ， ， 均为双眼皮．【知识应用】现有一对夫妻，两人成对的基因都是 ， 若不考虑其他因素，则他们的孩子是单眼皮的概率是（ ）
A、 B、 C、 D、7. 校篮球队员小亮训练定点投篮以提高命中率．下表是小亮一次训练时的进球情况：投篮数（次）
50
100
150
200
…·
进球数（次）
40
81
118
160
…
则下列说法正确的是（ ）
A、小亮每投10个球，一定有8个球进 B、小亮投球前8个进，第9，10个一定不进 C、小亮比赛中的投球命中率一定为80% D、小亮比赛中投球命中率可能超过80%8. 班长邀请A，B，C，D四位同学参加圆桌会议．如图，班长坐在⑤号座位，四位同学随机坐在①②③④四个座位，则A，B两位同学座位相邻的概率是（ ）
A、 B、 C、 D、9. 有三条带子，第一条的一头是黑色，另一头是黄色，第二条的一头是黄色，另一头是白色，第三条的一头是白色，另一头是黑色．若任意选取这三条带子的一头，颜色各不相同的概率是（ ）．
A、 B、 C、 D、10. 设x，y，z为三个不同的整数，x，y，z∈{1，2，3，……，2016} ，则下列关于xyz为奇数的概率P的说法中，正确的是（ ）A、P< B、P= C、<P< D、P= E、P>二、填空题（本题有6小题，每小题4分，共24分）
-
11. 为考察一种枸杞幼苗的成活率，在同一条件下进行移植试验，结果如下表所示：
移植总数
40
150
300
500
700
1000
1500
成活数
35
134
271
451
631
899
1350
成活的频率
0.875
0.893
0.903
0.902
0.901
0.899
0.900
估计这种幼苗移植成活的概率是(结果精确到0.1).
12. 如图是一个游戏转盘，连续自由转动转盘两次（如果落在分隔线上，则重新转动，直至转到其中一块区域），则两次转动指针都落在数字“蓝色”所示区域内的概率是 ．
13. 在如图所示的电路中，同时闭合两个开关能使小灯泡发光的概率是.
14. 在平面直角坐标系中，作△OAB，其中三个顶点分别是O(0，0)，B(1，1)，A(x，y)(－2≤x≤2，－2≤y≤2，x，y均为整数)，则所作△OAB为直角三角形的概率是 ．15. 数学作业本分为上、下各1册，小明随机将它们叠放在一起，从上到下的顺序恰好为“上册、下册”的概率是 ．16. 如图是 正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中任选出一个也涂成黑色，则使整个涂黑部分为轴对称图形的概率是.
三、解答题（本题共8小题，第17题6分，第18题6分，第19题13分，第20题6分，第21题6分，第22题7分，第23题12分，第24题10分，共66分）
-
17. 物理变化和化学变化的区别在于是否有新物质的生成．某学习小组在延时课上制作了A ， B ， C ， D四张卡片，四张卡片除图片内容不同外，其他没有区别，放置于暗箱中摇匀．
(1)、小临从四张卡片中随机抽取一张，抽中C卡片的概率是；(2)、小夏从四张卡片中随机抽取两张，用列表法或画树状图法求小夏抽取两张卡片内容均为化学变化的概率．18. 一个不透明的袋子中共装有五个小球，其中3个红球，1个白球，1个黄球，这些小球除颜色外都相同．将袋中小球摇匀，从中随机摸出一个小球记下颜色后放回，记作随机摸球一次．(1)、随机摸球10次，其中摸出黄球3次，则这10次摸球中，摸出黄球的频率是 ．(2)、随机摸球2次，用画树状图或列表的方法，求这两次摸出的小球都是红球的概率．19. 某校田径队为了调动队员体育训练的积极性，计划根据成绩情况对队员进行奖励.为确定一个适当的成绩目标，进行了体育成绩测试，统计了每个队员的成绩，数据如下：收集数据
77
78
76
72
84
75
91
85
78
79
82
78
76
79
91
91
76
74
75
85
75
91
80
77
75
75
87
85
76
77
整理、描述数据
成绩/分
72
74
75
76
77
78
79
80
82
84
85
87
91
人数/人
1
1
a
4
3
3
b
1
1
1
3
1
4
分析数据样本数据的平均数、众数、中位数如下表：
平均数
众数
中位数
80
c
78
解决问题
(1)、表格中的；；；(2)、分析平均数、众数、中位数这三个数据，如果想让一半左右的队员都能达到成绩目标，你认为成绩目标应定为分，如果想确定一个较高的成绩目标，这个成绩目标应定为分；(3)、学校要从91分的A ， B ， C ， D四名队员中，随机抽取两名队员去市里参加系统培训.请利用画树状图法或列表法，求A ， B两名队员恰好同时被选中的概率.20.(1)、概念理解嘉嘉和淇淇学习了随机事件的概率，老师留的作业中有一道判断题：①自然现象中，“太阳从东方升起”是必然事件；②成语“水中捞月”所描述的事件是随机事件；③若抽奖活动的中奖概率为 ， 则抽奖50次必中奖1次．
真命题的序号是；
(2)、知识应用嘉嘉和淇淇做化学实验，紫色石蕊试剂是一种常用的酸碱指示剂，通常情况下石蕊试剂遇酸溶液变红，遇碱溶液变蓝，遇中性溶液不变色．现有4瓶缺失标签的无色液体：蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液，其中白醋溶液、柠檬水溶液是酸性，食用碱溶液是碱性，蒸馏水是中性，两人各取了4个烧杯，分别倒入这4种不同的无色液体．
①嘉嘉将石蕊试剂滴入任意一个烧杯，呈现蓝色的概率是 ；
②淇淇随机取了两个烧杯，滴入石蕊试剂，用画树状图法或列表法求一杯变红、一杯变蓝的概率．
21. “校园诗歌大赛”结束后，张老师和李老师将所有参赛选手的比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数直方图部分信息如图：
(1)、成绩前三名是2名男生和1名女生，若从他们中任选2人作为获奖代表发言，试求恰好选中1男1女的概率．(2)、赛前规定，成绩由高到低前 的参赛选手获奖．某参赛选手的比赛成绩为78分，试判断他能否获奖，并说明理由．22. 问题情境：在数学探究活动中，老师给出了如图的图形及下面三个等式：① ② ③ 若以其中两个等式作为已知条件，能否得到余下一个等式成立？
解决方案：探究 与 全等．
问题解决：
(1)、当选择①②作为已知条件时， 与 全等吗？（填“全等”或“不全等”），理由是；(2)、当任意选择两个等式作为已知条件时，请用画树状图法或列表法求 的概率．23. 我市某中学举行“中国梦·我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题.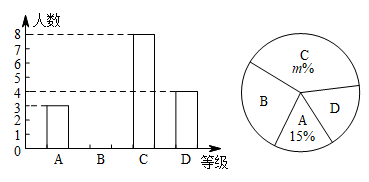
(1)、参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；(2)、补全条形统计图；(3)、组委会决定从本次比赛中获得A等级的学生中，选出两名去参加市中学生演讲比赛，已知A等级中男生只有1名，请用画树状图或列表的方法求出所选学生恰是一男一女的概率.24.某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
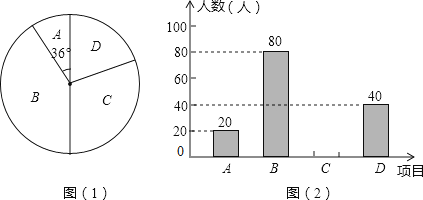(1)、这次被调查的学生共有 人；
(2)、请你将条形统计图（2）补充完整；
(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率.（用树状图或列表法解答）