【提升版】浙教版数学九上2.3用频率估计概率 同步练习
试卷更新日期：2024-07-31 类型：同步测试
一、选择题
-
1. 已知抛一枚均匀硬币正面朝上的概率为 ， 下列说法错误的是（ ）A、大量反复抛一均匀硬币，平均100次出现正面朝上50次 B、连续抛一均匀硬币10次都可能正面朝上 C、连续抛一均匀硬币2次必有1次正面朝上 D、通过抛一均匀硬币确定谁先发球的比赛规则是公平的2. 在同样的条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表，由表估计该麦种的发芽概率是（ ）
试验种子数n（粒）
50
200
500
1000
3000
发芽频数m
45
188
476
951
2850
发芽频率
0.9
0.94
0.952
0.951
0.95
A、0.8 B、0.9 C、0.95 D、13. 甲、乙两名同学在一次大量重复试验中，统计了某一结果出现的频率，绘制出的统计图如图所示，符合这一试验结果的可能是（ ）
A、掷一枚质地均匀的骰子，出现1点朝上的概率 B、从一个装有大小相同的2个白球和1个红球的不透明袋子中随机取一球，取到红球的概率 C、抛一枚1元钱的硬币，出现正面朝上的概率 D、从标有数字1到10的十张大小相同的纸牌中随机抽取一张，是2的倍数的概率4. 种子被称作农业的“芯片”，关系到国家粮食安全．某种业公司培育成功了两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培有环境中分别实验，实验情况记录如下：种子数量 200 500 800 1500 3000 A 出芽率 0.98 0.94 0.96 0.98 0.97 B 出芽率 0.98 0.95 0.94 0.97 0.96 下面在三个推断：
①当实验种子数员为200时，两种种子的出芽率均为0.98，所以两种新五米种子出芽的概率一样；
②随着实验种子数量的增加，种子出芽率在0.96附近摆动，显示出一定的稳定性，可以估计种子出芽的概率是0.96：
③在同样的地质环境下播种，种子的出芽率可能会离于种子．
其中合理的是（ ）
A、①②③ B、①② C、②③ D、①③5. 为迎接六一儿童节到来，某商场规定凡是购物满88元以上都可以获得一次转动转盘的机会.如图①所示，当转盘停止时，指针指向哪个区域顾客就获得对应的奖品.转动转盘若干次，其中指针落入优胜奖区域的频率如图②所示，则转盘中优胜奖区域的圆心角∠AOB的度数近似为（ ）
A、90° B、72° C、54° D、20°6. 数学课上，李老师与学生们做“用频率估计概率”的试验：不透明袋子中有5个白球、3个红球和2个黄球，这些球除颜色外无其他差别．从袋子中随机取出一个球，某种颜色的球出现的频率如图所示，则该球的颜色最有可能是（ ）
A、黑球 B、黄球 C、红球 D、白球7. 有一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同。小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是（ ）A、6 B、16 C、18 D、248. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．（注：）
下面有四个推断：
①当投掷次数是600时，计算机记录“钉尖向上”的次数是400，所以“钉尖向上”的概率是0.667；
②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620；
④若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的情况一定高于500次．
其中合理的是（ ）
A、① B、② C、③ D、④二、填空题
-
9. 在一个四宫格火锅里有三种锅底，一种是清汤锅底，一种是麻辣锅底．一种是红汤锅底，服务员将100粒丸子随机投入四个宫格中，就餐的小伙伴数了数，结果有49粒是清汤味的，估计倒入红汤锅底的丸子数是 ．
10. 某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼，鱼塘主通过多次捕捞试验发现，捕捞到鲫鱼的频率稳定在0.25左右。若鱼塘主随机在鱼塘里捕捞一条鱼，捕捞到草鱼的概率约为.11. 十八世纪法国的博物学家C·布丰做过一个有趣的投针试验．如图，在一个平面上画一组相距为的平行线，用一根长度为的针任意投掷在这个平面上，针与直线相交的概率为 ， 可以通过这一试验来估计的近似值．某数学兴趣小组利用计算机模拟布丰投针试验，取 ， 得到试验数据如下表：
试验次数
1500
2000
2500
3000
3500
4000
4500
5000
相交频数
495
623
799
954
1123
1269
1434
1590
相交频率
可以估计出针与直线相交的概率为（精确到），由此估计的近似值为（精确到）．
12. 水稻育秧前都要提前做好发芽试验，特别是高水分种子，确保发芽率达到以上，保证成苗率，现有 ， 两种新水稻种子，为了解它们的发芽情况，在推广前做了五次发芽实验，每次随机各自取相同的种子数，在相同的培育环境中分别实验，实验情况记录如下：种子数量
发芽率
发芽率
下面有两个推断：
当实验种子数量为时，两种种子的发芽率均为 ， 所以 ， 两种新水稻种子发芽的概率一样；
随着实验种子数量的增加，种子发芽率在附近摆动，显示出一定的稳定性，可以估计种子发芽的概率是 ． 其中合理的是 ．三、解答题
-
13. 为了“天更蓝，水更绿”，湘潭市政府加大了对空新污染的治理力度，经过几年的努力，空气质量明显改善。市环保局随机五30天空气质增指数（AQI），绘制成扇形统计图．
空气质量等级
空气质量指数（AQI）
频数
优
AQI≤50
m
良
50＜AQI＜1100
15
中
100＜AQI≤150
9
差
AQI>150
n
(1)、m= ，n=；(2)、求良的占比；(3)、求差的圆心角；(4)、请根据样本数据，估测该城市一年（以360天计）中大约有天AQI为中.14. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复如表是活动进行中的一组统计数据：摸球的次数
摸到白球的次数
摸到白球的频率
(1)、上表中的 ， ；
(2)、“摸到白球”的概率的估计值是精确到；
(3)、如果袋中有个白球，那么袋中除了白球外，还有多少个其它颜色的球．15. 某同学用计算机从3，4，5，x这四个数中，随机同时抽取两个数，多次重复实验后的数据记录如下：实验总次数
10
50
100
500
1000
2000
5000
10000
20000
50000
“和为8”的次数
2
25
43
191
334
619
1608
3397
6622
16499
“和为8”的频率（结果保留两位小数）
0.20
0.50
0.43
0.38
0.33
0.31
0.32
0.34
0.33
0.33
(1)、随着实验次数的增加，出现“和为8”的频率将越来越稳定于它的概率附近．由此可以估计出现“和为8”的概率是；(2)、当时，请用列表法或画树状图法中的一种方法，求“两数之和为8”的概率．四、综合题
-
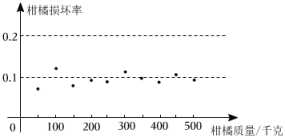
16. 某水果公司以9元/千克的成本从果园购进10000千克特级柑橘，在运输过程中，有部分柑橘损坏，该公司对刚运到的特级柑橘进行随机抽查，并得到如下的“柑橘损坏率”统计图．由于市场调节，特级柑橘的售价与日销售量之间有一定的变化规律，如下表是近一段时间该水果公司的销售记录．
特级柑橘的售价(元/千克) 14 15 16 17 18 特级柑橘的日销售量(千克) 1000 850 900 850 800 (1)、估计购进的10000千克特级柑橘中完好的柑橘的总重量为千克；(2)、按此市场调节的规律来看，若特级柑橘的售价定为16.5元每千克，估计日销售量，并说明理由．(3)、考虑到该水果公司的储存条件，该公司打算12天内售完这批特级柑橘只售完好的柑橘 ， 且售价保持不变，求该公司每日销售该特级柑橘可能达到的最大利润，并说明理由．