【培优版】新北师大版(2024)数学七上 4.1线段、射线、直线 同步练习
试卷更新日期：2024-07-28 类型：同步测试
一、选择题
-
1. 平面内的9条直线任两条都相交，交点数最多有m个，最少有n个，则m+n等于（ ）A、36 B、37 C、38 D、392. 如果线段AB=13cm，MA+MB=17 cm，那么下面说法中正确的是（ ）.A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上，也可能在直线AB外3. 点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于（ ）A、3 B、2 C、3或5 D、2或64. 有三个点A，B，C，过其中每两个点画直线，可以画出直线（ ）A、1条 B、2条 C、1条或3条 D、无法确定5. 如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（ ）A、4cm B、2cm C、4cm或2cm D、小于或等于4cm，且大于或等于2cm6. 生活中，有下列两个现象，对于这两个现象的解释，正确的是（ ）
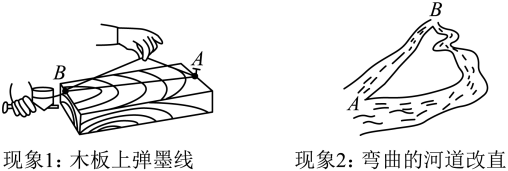A、均用两点之间线段最短来解释 B、均用经过两点有且只有一条直线来解释 C、现象1用两点之间线段最短来解释，现象2用经过两点有且只有一条直线来解释 D、现象1用经过两点有且只有一条直线来解释，现象2用两点之间线段最短来解释7. 平面内有五个点，过每两个点作一条直线，可以作的直线条数不可能是（ ）A、5 B、6 C、7 D、88. 下列说法中，正确的有（ ）个①过两点有且只有一条直线 ②连接两点的线段叫做两点间的距离
③两点之间，线段最短 ④若AB=BC，则点B是线段AC的中点
⑤射线AB和射线BA是同一条射线 ⑥直线有无数个端点．
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点．点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P最多有个．
10. 在的内部引一条射线，图中共有3个角；若引两条射线，图中共有6个角；若引n条射线，图中共有个角．
11. 在平面上有三点，过其中任意两点画直线，可画直线的条数为条.12. 如图，该图中不同的线段共有条.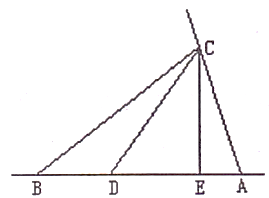
13. 若在直线 上取6个点，则图中一共出现条射线和 线段.三、作图题
-
14. 如图
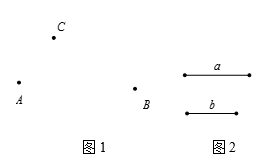(1)、如图1，平面上有3个点A，B，C．①画直线AB；画射线BC；画线段AC；
②过点C作AB的垂线，垂足为点D；
③量出点C到直线AB的大约距离．
(2)、尺规作图：已知：线段a，b，如图2．
求作：一条线段MN，使它等于2a－b．（不写作法，保留作图痕迹）
四、解答题
-
15. ① 如图（1），直线l上有2个点，则图中有2条可用图中字母表示的射线：A1A2、A2A1 ， 有1条线段：A1A2；
② 如图（2），直线l上有3个点，则图中有几条可用图中字母表示的射线，有几条线段，并分别用图中字母表示出来；
③ 如图（3），直线l上有n个点，则图中有多少条可用图中字母表示的射线，有多少条线段，分别用含n的代数式表示出来；
④ 应用（3）中发现的规律解决问题：某校七年级共有8个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需多少场比赛？
16. 按要求作图并回答问题：已知：如图点A，点B，点C．
(1)、作直线 ， 射线 ， 线段；(2)、在点C的东北方向有一点D，且点D在直线上，画出点D；(3)、点P，Q以同样的速度同时从A点向C点运动，点P沿线段AC运动，点Q沿A---B---C的路线运动，请你判断谁先到达点C：（填“点P”或“点Q”），理由是 ；(4)、已知线段 ， 若点P以的速度从点A出发沿射线方向运动，同时点Q以的速度从点B出发向A运动，M、N分别是与的中点，请通过计算说明M、N两点是否可以重合？若能重合，请求出所需要的时间和重合时线段的长．17.如图所示，线段AB上的点数与线段的总数有如下关系：如果线段AB上有3个点时，线段总数共有3条，如果AB上有4个点时，线段总数共有6条，如果线段AB上有5个点时，线段总数共有10条，…．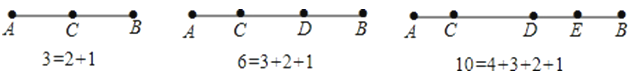
（1）当线段AB上有6个点时，线段总数共有多少条？
（2）当线段AB上有n个点时，线段总数共有多少条？（用含n的式子表示）
（3）当n=100时，线段总数共有多少条？
-