人教版八年级上学期数学第十一章质量检测(高阶)
试卷更新日期:2024-07-28 类型:单元试卷
一、选择题
-
1. 多边形的每一个外角都是 , 则此多边形从一个顶点出发的对角线有( )条.A、7条 B、8条 C、9条 D、10条2. 小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( )
 A、 B、 C、 D、3. 五条长度均为整数厘米的线段:a1 , a2 , a3 , a4 , a5 , 满足a1<a2<a3<a4<a5 , 其中a1=1厘米,a5=9厘米,且这五条线段中的任意三条都不能构成三角形,则a3=( )A、3厘米 B、4厘米 C、3或4厘米 D、不能确定4. 如图,在△ABC中,BE平分∠ABC交AC于点E , CD⊥AC交AB于点D , ∠BCD=∠A , 则∠BEA的度数( )
A、 B、 C、 D、3. 五条长度均为整数厘米的线段:a1 , a2 , a3 , a4 , a5 , 满足a1<a2<a3<a4<a5 , 其中a1=1厘米,a5=9厘米,且这五条线段中的任意三条都不能构成三角形,则a3=( )A、3厘米 B、4厘米 C、3或4厘米 D、不能确定4. 如图,在△ABC中,BE平分∠ABC交AC于点E , CD⊥AC交AB于点D , ∠BCD=∠A , 则∠BEA的度数( )
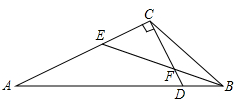 A、155° B、135° C、108° D、100°5. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A、155° B、135° C、108° D、100°5. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( ) A、180° B、360 C、270° D、540°6. 如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1BlC1的面积是( )
A、180° B、360 C、270° D、540°6. 如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1BlC1的面积是( )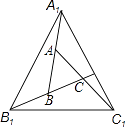 A、4 B、5 C、6 D、77. 有一块直角三角尺DEF放置在△ABC上,三角尺DEF的两条直角边DE , DF恰好分别经过点B , C . 在△ABC中,若 , 则∠A的度数是( )
A、4 B、5 C、6 D、77. 有一块直角三角尺DEF放置在△ABC上,三角尺DEF的两条直角边DE , DF恰好分别经过点B , C . 在△ABC中,若 , 则∠A的度数是( )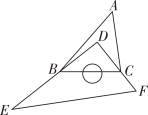 A、40° B、44° C、45° D、50°8. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD = 90°, ④∠ADB= 45°-∠CDB,其中正确的结论有( )
A、40° B、44° C、45° D、50°8. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD = 90°, ④∠ADB= 45°-∠CDB,其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个9. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个9. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )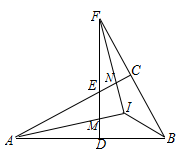 A、1个 B、2个 C、3个 D、4个10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,小明从A点出发前进10m,向右转15°,再前进10 m,又向右转15°,…,这样一直走下去,他第一次[回到出发点A时,一共走了m。
 12. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为.
12. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为. 13. 如图,△ABC的面积为18,BD=2DC,AE=2EC,那么阴影部分的面积是。
13. 如图,△ABC的面积为18,BD=2DC,AE=2EC,那么阴影部分的面积是。 14. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= , △APE的面积等于6.
14. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= , △APE的面积等于6.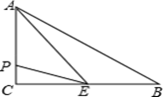 15. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为 .
15. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为 .
三、解答题
-
16. 如图,已知AD,AE分别是△ABC的高和中线,AB=3cm,AC=4cm,BC=5cm,∠CAB=90°,求:
 (1)、AD的长;(2)、△ACE和△ABE的周长的差.17. 如图1,已知∠MON=60° , A、B两点同时从点O出发,点A沿射线ON运动,点B沿射线OM运动.,点C为△ABO三条内角平分线交点,连接BC、AC .
(1)、AD的长;(2)、△ACE和△ABE的周长的差.17. 如图1,已知∠MON=60° , A、B两点同时从点O出发,点A沿射线ON运动,点B沿射线OM运动.,点C为△ABO三条内角平分线交点,连接BC、AC . (1)、如图2,当∠OAB=70° , 求∠ACB的大小。(2)、在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由:(3)、如图3,连接OC并延长,与∠ABM的角平分线交于点P , 与AB交于点Q . 在△BCP中,如果有一个角是另一个角的2倍,直接写出∠BAO的度数.
(1)、如图2,当∠OAB=70° , 求∠ACB的大小。(2)、在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由:(3)、如图3,连接OC并延长,与∠ABM的角平分线交于点P , 与AB交于点Q . 在△BCP中,如果有一个角是另一个角的2倍,直接写出∠BAO的度数.四、实践探究题
-
18.
 (1)、【课本再现】如图1,在中,线经过点且 . 求证:;(2)、【变式演练】如图2,在中, , 点在边上,交于点 . 若 , 求的度数;(3)、【方法应用】如图3,直线与直线相交于点 , 夹角的锐角为 , 点在直线上且在点右侧,点在直线上且在直线上方,点在直线上且在点左侧运动,点在射线上运动(不与点重合).当时,平分平分交直线于点 , 求的度数.19. 探究与发现:
(1)、【课本再现】如图1,在中,线经过点且 . 求证:;(2)、【变式演练】如图2,在中, , 点在边上,交于点 . 若 , 求的度数;(3)、【方法应用】如图3,直线与直线相交于点 , 夹角的锐角为 , 点在直线上且在点右侧,点在直线上且在直线上方,点在直线上且在点左侧运动,点在射线上运动(不与点重合).当时,平分平分交直线于点 , 求的度数.19. 探究与发现: (1)、如图1,在中, , 分别平分和 .
(1)、如图1,在中, , 分别平分和 .①若 , 则;
②若 , 用含有的式子表示的度数为;
(2)、如图2,在四边形中, , 分别平分和 , 试探究与的数量关系,并说明理由;(3)、如图3,在六边形中, , 分别平分和 , 请直接写出与的数量关系.20. (1)、【问题背景】小强在学习完平行线一节后,想利用平行线的知识证明“三角形的内角和是180°”;.如图1,是小强为证明三角形内角和是180°所采取的构图方法:过△ABC的顶点A作EF∥BC .
(1)、【问题背景】小强在学习完平行线一节后,想利用平行线的知识证明“三角形的内角和是180°”;.如图1,是小强为证明三角形内角和是180°所采取的构图方法:过△ABC的顶点A作EF∥BC .请完成:利用小强的构图,说明∠BAC+∠B+∠C=180°的理由;
(2)、【尝试应用】如图2,直线l1与直线l2相交于点O , 夹角为α,点B在点O右侧,点C在l1上方,点A在O点左侧运动,点E在射线CO上运动(不与C , O重合);请完成:当α=60°时,AG平分∠EAB , EF平分∠AEC交直线AG于点G , 求∠AGE的度数;
(3)、【拓展创新】如图3,点E在线段CO上运动(不与C , O重合),∠AEF=n∠AEC , ∠EAG=m∠EAB , m+2n=1,EF交AG于点G;请完成:当n为何值时,∠AGE不随∠EAB的变化而变化,并用含α的代数式表示∠AGE的度数(写出解答过程).
21. 【问题呈现】如图①,已知线段 , 相交于点 , 连结 , , 我们把形如这样的图形称为“字型”.
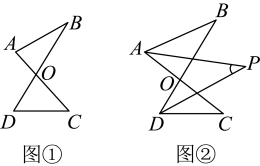 (1)、证明: .(2)、【问题探究】
(1)、证明: .(2)、【问题探究】继续探究,如图②,、分别平分、 , 、交于点 , 求与、之间的数量关系.为了研究这一问题,尝试代入、的值求的值,得到下面几组对应值:
表中 , 猜想得到与、的数量关系为;
(3)、证明()中猜想得到的与、的数量关系;(单位:度)
(单位:度)
(单位:度)