人教版八年级上学期数学第十一章质量检测（进阶）

试卷更新日期：2024-07-28 类型：单元试卷

进入出卷网下载

一、选择题（共30分，每题3分）

1. 在△ABC中，若∠A+∠B－∠C＝0，则△ABC是（）

A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
2. 一个正多边形的每一个内角是 $135 °$ ，则从这个正多边形的一个顶点出发可作（）条对角线．

A、5 B、4 C、3 D、2

查看试题解析
3. 若一个三角形的三条边长分别为3，2a-1，6，则整数a的值可能是（）

A、2，3 B、3，4 C、2，3，4 D、3，4，5

查看试题解析
4. 如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）

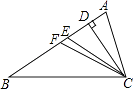A、AB=2BF B、∠ACE= $\frac{1}{2}$ ∠ACB C、AE=BE D、CD⊥BE

查看试题解析
5. 下列几种形状的瓷砖中，只用一种不能够铺满地面的是（　　）

A、正六边形 B、正五边形 C、正方形 D、正三角形

查看试题解析
6. 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（）

A、180° B、270° C、360° D、720°

查看试题解析
7. 如图，七边形ABCDEFG中，AB、ED的延长线交于点O，若∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析

二、填空题（共15分，每题3分）

8. 如图，在 $△ A B C$ 中， $∠ A = 6 0^{∘}$ ， $∠ 1 = 2 0^{∘}$ ， $∠ 2 = 3 0^{∘}$ ，则 $∠ B D C$ 的度数是

查看试题解析
9. 如图，一束光沿CD方向，先后经过平面镜OB、OA反射后，沿EF方向射出，已知∠A0B＝120°∠CDB＝20°，则∠AEF＝．

查看试题解析
10. 如图， $∠ 1$ 是五边形的一个外角．若 $∠ 1 = 70 °$ ，则 $∠ A + ∠ B + ∠ C + ∠ D$ 的度数为．

查看试题解析
11. 如图，在△ABC中，∠C＝47°，将△ABC沿着直线 $l$ 折叠，点C落在点D的位置，则∠1－∠2的度数是．

查看试题解析
12. 如图， $A E ⊥ E C$ 于点E ， $C D ⊥ A D$ 于点D ， AD交EC于点B．若 $A B = 5$ ， $B C = 2$ ， $C D = \frac{9}{5}$ ，则 $A E =$ ．

查看试题解析

三、解答题（共66题，16题6分，17题10分，22题10分，

13. 已知a，b，c是△ABC的三边长，若b＝2a﹣1，c＝a+5，且△ABC的周长不超过20cm，求a的范围.

查看试题解析
14. 设a，b，c是 $△ A B C$ 的三边，

(1)、化简 $| a - b - c | + | b + c - a | - | c - a - b |$

(2)、若b，c满足 ${(b - 2)}^{2} + | c - 3 | = 0$ ，且a为方程 $| x - 4 | = 2$ 的解，判断 $△ A B C$ 的形状并说明理由．

查看试题解析

15. 请阅读下列材料，并完成相应任务．

在数学探究课上，老师出了这样一个题：如图 $1$ ，锐角 $∠ B A C$ 内部有一点 $D$ ，在其两边 $A B$ 和 $A C$ 上各取任意一点 $E$ ， $F$ ，连接 $D E$ ， $D F$ ，求证： $∠ B E D + ∠ D F C = ∠ B A C + ∠ E D F$ ．

小丽的证法

小红的证法

证明：

如图 $2$ ，连接 $A D$ 并延长至点 $M$ ， $∠ B E D = ∠ B A D + ∠ E D A$ ， $∠ D F C = ∠ D A C + ∠ A D F$ （依据），

又∵ $∠ B A D + ∠ D A C = ∠ B A C$ ， $∠ E D A + ∠ A D F = ∠ E D F$ ，

∴ $∠ B E D + ∠ D F C = ∠ B A C + ∠ E D F$ ．

证明：

∵ $∠ B E D = 80 °$ ， $∠ D F C = 60 °$ ， $∠ B A C = 51 °$ ， $∠ E D F = 89 °$ （量角器测量所得），

∴ $∠ B E D + ∠ D F C = 140 °$ ，（计算所得）．

∴ $∠ B E D + ∠ D F C = ∠ B A C + ∠ E D F$ （等量代换）．

任务：

(1)、小丽证明过程中的“依据”是指数学定理：______；

(2)、下列说法正确的是______．

A．小丽的证法用严谨的推理证明了本题结论

B．小丽的证法还需要改变 $∠ B A C$ 的大小，再进行证明，本题的证明才完整

C．小红的证法用特殊到一般的方法证明了本题结论

D．小红的证法只要将点 $D$ 在 $∠ B A C$ 的内部任意移动 $100$ 次，重新测量进行验证，就能证明本题结论

(3)、如图

3

，若点

D

在锐角

∠ B A C

外部，

E D

与

A C

相交于点

G

，其余条件不变，原题中结论还成立吗？若成立，请说明理由；若不成立，请写出

∠ B E D

，

∠ D F C

，

∠ B A C

，

∠ E D F

之间的关系并证明．

查看试题解析

16.

(1)、如图1，在△ABC中，AD，AE分别是△ABC的高线和角平分线，已知∠B=30°，∠C=50°．求∠DAE的度数．

(2)、如图2，∠BAC的平分线AF交BC于点E，过点F作FD⊥BC于点D，若∠B=x°，∠C=（x+30）°．
①∠CAE= ▲ （含x的代数式表示）．
②求∠F的度数．

查看试题解析
17. 阅读下面材料：
“百年器象——清华大学科学博物馆筹备展”上展出了一件清华校友捐赠的历史文物“Husun型六分仪”（图①），它见证了中国人民解放军海军的发展历程，六分仪是测量天体高度的手提式光学仪器，它的主要原理是几何光学中的反射定律。观测者手持六分仪（图②）按照一定的观测步骤（图③显示的是其中第6步）读出六分仪圆弧标尺上的刻度，再经过一定计算得出观测点的地理坐标。
请大家证明在使用六分仪测量时用到的一个重要结论（两次反射原理）。
已知：在图④所示的“六分仪原理图”中，所观测星体记为S，两个反射镜面位于A，B两处，B处的镜面所在直线FBC自动与O°刻度线AE保持平行（即BC∥AE)，并与A处的镜面所在直线NA交于点C，SA所在直线与水平线MB交于点D，六分仪上刻度线AC与0°刻度线的夹角∠EAC=ω，观测角为∠SDM.(请注意小贴士中的信息)

(1)、猜想∠SDM与ω的数量关系。

(2)、请证明你的猜想。

查看试题解析

四、实践探究题（共9分）

18. 阅读与理解：
三角形的中线的性质：三角形的中线等分三角形的面积，即如图1，AD是△ABC中BC边上的中线，则S_△_ABD=S_△_AC_D= $\frac{1}{2}$ S_△AB_C ．
操作与探索：
在图2至图4中，△ABC的面积为a．

(1)、如图2，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S₁ ，则S₁= ．（用含a的代数式表示）．

(2)、如图3，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S₂ ，则S₂=（用含a的代数式表示）．

(3)、在图3的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图4）．若图4中△DEF的面积为S₃ ，则S₃=（用含a的代数式表示）．

查看试题解析