【培优版】北师大版数学九年级上册第二章一元二次方程章节测试卷

试卷更新日期：2024-07-28 类型：单元试卷

进入出卷网下载

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 用配方法解方程 $x^{2} - 4 x - 3 = 0$ ，下列配方结果正确的是（）．

A、 ${(x - 2)}^{2} = 7$ B、 ${(x - 4)}^{2} = 19$ C、 ${(x + 2)}^{2} = 7$ D、 ${(x + 4)}^{2} = 19$

查看试题解析
2. 设m是整数，关于x的方程mx²-（m-1）x+1=0有有理根，则方程的根为（）。

A、 $x_{1} = \frac{1}{2} ， x_{2} = \frac{1}{3}$ B、x=-1 C、 $x_{1} = - 1 ， x_{2} = \frac{1}{2} ， x_{3} = \frac{1}{3}$ D、有无数个根

查看试题解析
3. 已知菱形ABCD的边长为5，两条对角线交于O点，且OA、OB的长分别是关于 $x$ 的方程 $x^{2} + (2 m - 1) x + m^{2} + 3 = 0$ 的根，则m等于（）

A、 $- 3$ B、 $5$ C、 $5 或 - 3$ D、 $- 5 或 3$

查看试题解析
4. 已知 $△ A B C$ 的三边长为a，b，c，且满足方程a²x²-（c²-a²-b²）x+b²=0，则方程根的情况是（）。

A、有两相等实根 B、有两相异实根 C、无实根 D、不能确定

查看试题解析
5. 如果关于x的一元二次方程x²﹣4|a|x+4a²﹣1=0的一个根是5，则方程的另一个根是（　　）

A、1 B、5 C、7 D、3或7

查看试题解析
6. 如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是(　　)

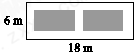A、x²＋9x－8＝0 B、x²－9x－8＝0 C、x²－9x＋8＝0 D、2x²－9x＋8＝0

查看试题解析
7. 一个三角形的两边长是2和6，第三边长是方程 $x^{2} - 10 x + 21 = 0$ 的根，则这个三角形的周长为（）

A、15 B、11 C、11或15 D、无法确定

查看试题解析
8. 对于一元二次方程ax²+bx+c＝0（a≠0），下列说法：①若a+b+c＝0，则b²﹣4ac≥0；②若方程ax²+c＝0有两个不相等的实根，则方程ax²+bx+c＝0必有两个不相等的实根；③若c是方程ax²+bx+c＝0的一个根，则一定有ac+b+1＝0成立；④若x₀是一元二次方程ax²+bx+c＝0的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ ；其中正确的（）

A、只有①② B、只有①②④ C、①②③④ D、只有①②③

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. 一个等腰三角形的底边长为10，腰长是一元二次方程 $x^{2} - 11 x + 30 = 0$ 的一个根，则这个三角形的周长是.

查看试题解析
10. 在实数范围内定义一种运算“*”，其规则为a*b=a²﹣b² ，根据这个规则，方程（x+2）*5=0的解为．

查看试题解析
11. 若关于x的方程(a+1)x²+(2a﹣3)x+a﹣2＝0有两个不相等的实根，且关于x的方程 $\frac{a x}{1 + x} - 1 = \frac{3}{x + 1}$ 的解为整数，则满足条件的所有整数a的和是．

查看试题解析
12. 已知实数 $α$ ， $β$ 满足 $2 α^{2} + 5 α - 2 = 0$ ， $2 β^{2} - 5 β - 2 = 0$ ，且 $α β \neq 1$ ，且 $\frac{1}{β^{2}} + \frac{α}{β} - \frac{5}{2} α$ 的值为．

查看试题解析
13. 对于一切不小于2的自然数n，关于x的一元二次方程x²﹣（n+2）x﹣2n²=0的两个根记作a_n ， b_n（n≥2）， $\frac{1}{(a_{2} - 2) (b_{2} - 2)} + \frac{1}{(a_{3} - 2) (b_{3} - 2)}$ $+ \dots +$ $\frac{1}{(a_{2020} - 2) (b_{2020} - 2)}$ = ．

查看试题解析

三、解答题（共7题，共53分）

14. 解方程．

(1)、 $x (x + 1) - 2 (x + 1) = 0$ ；

(2)、 $x^{2} + 4 x - 1 = 0$ ．

查看试题解析
15. 已知关于 $x$ 的一元二次方程： $k^{2} x^{2} + (1 - 2 k) x + 1 = 0$ 有两个不相等的实数根.

(1)、求 $k$ 的取值范围；

(2)、若原方程的两个实数根为 $x_{1} ， x_{2}$ ，且满足 $| x_{1} | + | x_{2} | = 2 x_{1} x_{2} - 3$ ，求 $k$ 的值.

查看试题解析
16. 已知关于x的一元二次方程 $x^{2} + (m + 3) x + m + 1 = 0$ ．

(1)、求证：无论 $m$ 取何值，原方程总有两个不相等的实数根；

(2)、若 $x_{1} ， x_{2}$ 是原方程的两根，且 $| x_{1} - x_{2} | = 2 \sqrt{5}$ ，求 $m$ 的值．

查看试题解析
17. 阅读下列材料，解答问题：
材料：若 $x_{1} ， x_{2}$ 为一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根，则 $x_{1} + x_{2} = - \frac{b}{a} ， x_{1} \cdot x_{2} = \frac{c}{a}$ ．

(1)、已知实数 $m ， n$ 满足 $3 m^{2} - 5 m - 2 = 0 ， 3 n^{2} - 5 n - 2 = 0$ ，且 $m \neq n$ ，求 $m^{2} n + m n^{2}$ 的值．
解：根据题意，可将 $m ， n$ 看作方程 $3 x^{2} - 5 x - 2 = 0$ 的两个实数根．
∴ $m + n =$ ， $m n =$ ．
∴ $m^{2} n + m n^{2} = m n (m + n) =$ ．

(2)、已知实数 $a ， b$ 满足 $a^{2} = 2 a + 3 ， 9 b^{2} = 6 b + 3$ ，且 $a \neq 3 b$ ，求 $a b$ 的值．

(3)、已知实数 $m ， n$ 满足 $m + m n + n = \frac{a^{2}}{4} - 6 ， m - m n + n = - \frac{a^{2}}{4} + 2 a$ ，求实数 $a$ 的最大整数值．

查看试题解析
18. 阅读下面的材料，解答问题．
材料：解含绝对值的方程： $x^{2} - 3 | x | - 10 = 0$ ．

解：分两种情况：

①当 $x \geq 0$ 时，原方程化为 $x^{2} - 3 x - 10 = 0$ ，解得 $x_{1} = 5$ ， $x_{2} = - 2$ （舍去）；

②当 $x < 0$ 时，原方程化为 $x^{2} + 3 x - 10 = 0$ ，解得 $x_{3} = - 5$ ， $x_{4} = 2$ （舍去）．

综上所述，原方程的解是 $x_{1} = 5$ ， $x_{2} = - 5$ ．

请参照上述方法解方程 $x^{2} - | x + 1 | - 1 = 0$ ．

查看试题解析
19. “小龙虾”是我县特色农业的拳头产品，在南县被广泛养殖.2020年估计某村养殖面积有100亩，到2022年该村养殖面积达到196亩．

(1)、求该村这两年“小龙虾”养殖面积的平均增长率；

(2)、某养殖户调查发现，当“小龙虾”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出50千克．为了推广宣传，该养殖户决定降价促销，同时减少存量，已知“小龙虾”的平均成本为12元/千克，若要确保每天获利1750元，则售价应该降低多少元？

查看试题解析
20. $x_{1} ， x_{2}$ 是一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根，若满足 $| x_{1} - x_{2} | = 1$ ，则称此类方程为“差根方程”。根据“差根方程”的定义，解决下列问题：

(1)、通过计算，判断下列方程是不是“差根方程”：
① $x^{2} - 4 x - 5 = 0$ ② $2 x^{2} - 2 \sqrt{3} x + 1 = 0$ .

(2)、已知关于x的方程 $x^{2} + 2 a x = 0$ 是“差根方程”，求a的值；

(3)、若关于x的方程 $a x^{2} + b x + 1 = 0$ (a，b是常数， $a > 0$ ）是“差根方程”，请探索a与b之间的数量关系．

查看试题解析

【培优版】北师大版数学九年级上册第二章 一元二次方程 章节测试卷

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题（共7题，共53分）

【培优版】北师大版数学九年级上册第二章一元二次方程章节测试卷