【基础版】北师大版数学九上 2.6一元二次方程的应用 同步练习

试卷更新日期：2024-07-25 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为23万元，5月份售价为16万元，设该款汽车这两月售价的月均下降率是x ， 则所列方程正确的是（ ）
    A、16(1+x)2=23 B、23(1−x)2=16 C、16(1+2x)2=23 D、23(1−2x)2=16

    查看试题解析

  • 2. 一个微信群里共有x个好友，每个好友都分别给群里的其他好友发一条信息，共发信息756条，则可列方程（ ）
    A、12x(x−1)=756 B、12x(x+1)=756 C、x(x−1)=756 D、x(x+1)=756

    查看试题解析

  • 3. 某工厂生产一种产品，第一季度生产了10万件，由于市场供不应求，该工厂加大了产量，此后两个季度产量逐季度增加，前三个季度共生产36.4万件.已知第二季度和第三季度的增长率相同.设第二季度和第三季度的增长率为x ， 则可列正确的方程为（    ）
    A、10（1+x）2=36.4 B、10+10（1+x）2=36.4 C、10+10（1+x）+10（1+2x）=36.4 D、10+10（1+x）+10（1+x）2=36.4

    查看试题解析

  • 4. 某药品原价为100元，连续两次降价 a% 后，售价为64元，则 a 的值为（   ）
    A、10 B、20 C、23 D、36

    查看试题解析

  • 5. 如图，在一块长为22m ， 宽为17m的矩形地面内（两条道路分别与矩形的一条边平行），余下的铺上草坪，要使草坪的面积达到300m2 ， 设道路的宽为xm ， 可列方程为（    ）

      

    A、17×22−17x−22x=300 B、(22−x)(17−x)+x2=300 C、(22−x)(17−x)=300 D、2(22−x+17−x)=300

    查看试题解析

  • 6. 一个微信群里共有x个成员，每个成员都分别给群里的其他成员发一条信息，共发信息72条，则可列方程为（    ）
    A、12x(x−1)=72 B、12x(x+1)=72 C、x(x−1)=72 D、x(x+1)=72

    查看试题解析

  • 7. 如图所示，用10米的铁丝网围成一个面积为15的矩形菜地，菜地的一边靠墙（不使用铁丝），如果设平行于围墙的一边为x米，那么可列方程（    ）

    A、x(10−x)=15 B、x2(10−x)=15 C、x(10−12x)=15 D、x2(10−2x)=15

    查看试题解析

  • 8. 如图，有一长为12cm，宽为8cm的矩形纸片，在它的四角各剪去一个同样的小正方形，然后折叠成一个无盖的长方形纸盒，若纸盒的底面（图中阴影部分）的面积为36cm2 ， 求剪去的小正方形的边长，设剪去的小正方形的边长为xcm，根据题意可列方程为（ ）

    A、12×8−4×8x=36 B、(12−2x)(8−2x)=36 C、(12−x)(8−x)=36 D、12×8−4x2=36

    查看试题解析

二、填空题

  • 9. 某商品经过两次降价，每件零售价由60元降为38.4元．已知每次降价的百分率均为x ， 根据题意，可列方程为 ．

    查看试题解析

  • 10. “渝太太”“吖嘀吖嘀”等零售公司这几年在潼南迎来了蓬勃发展，其商品以价格亲民，品质较好，品种多样吸引了大量的顾客，今年4月份，潼南区江北一零售公司实现月纯利润为5万元，到6月份就突破到月纯利润为7.2万元，若该公司由4月份到6月份纯利润的月平均增长率为x ， 根据题意，列出方程为。

    查看试题解析

  • 11. 一种药品原价每盒25元，经过两次降价后每盒16元.若两次降价的百分率都为x ， 则根据题意可列方程.

    查看试题解析

  • 12. 某商场今年1月盈利3000万，3月盈利3630万，若从1月到3月，每月盈利的平均增长率都相同，则这个平均增长率是  ．

    查看试题解析

  • 13.  某商品经过两次降价，售价由原来的每件25元降到每件16元，该商品两次降价的百分率相同，若设平均每次降价的百分率为x ， 则可列方程为 ．

    查看试题解析

三、解答题

  • 14.  随着新能源汽车技术的提高，电能源汽车正逐渐成为人们喜爱的交通工具.某4S店新能源汽车销售量自2023年起逐月增加，据统计，该4S店1月份销售新能源汽车32辆，3月份销售了50辆.
    (1)、求该4S店这两个月的月平均增长率；
    (2)、若月平均增长率保持不变，求该4S店4月份卖出多少辆新能源汽车.（答案若含有小数则只取整数部分，不四舍五人）

    查看试题解析

  • 15. 果农张远原计划以每千克4元的单价销售某种水果，由于部分果农盲目扩大种植，造成该水果滞销，张远为了加快销售，减少损失，经过两次下调价格后，以每千克2.56元的单价销售。
    (1)、求平均每次下调价格的百分率；
    (2)、若张远第一次下调价格后卖出3吨该水果，第二次下调价格后又卖出2吨该水果，张远共获得销售款多少元？

    查看试题解析

  • 16. 如图1，某校准备一面利用墙，其余三面用篱笆围成一个矩形花圃ABCD，已知旧墙可利用的最大长度为13m，篱笆长为24m.

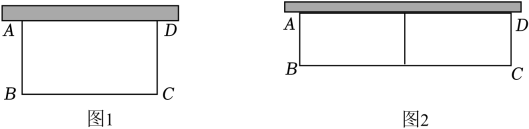    (1)、若围成的花圃面积为70m2 ， 求BC的长．
    (2)、如图2，若计划将花圃中间用一道篱笆隔成两个小矩形，且花圃面积为78m2 ， 请你判断能否围成这样的花圃．如果能，求BC的长；如果不能，请说明理由．

    查看试题解析

  • 17. 随着人民生活水平的不断提高，某小区家庭轿车的拥有量逐年增加.据统计，这个小区2010年底拥有家庭轿车144辆，2012年底家庭轿车的拥有量达到225辆.
    (1)、若该小区2010年底到2012年底家庭轿车拥有量的年平均增长率都相同，求该小区到2013年底家庭轿车将达到多少辆？
    (2)、为了缓解停车矛盾，该小区决定投资25万元再建造若干个停车位.据测算，建造费用分别为室内车位6000元/个，露天车位2000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的3倍，但不超过室内车位的4.5倍，求该小区最多可建两种车位各多少个？试写出所有可能的方案.

    查看试题解析

  • 18. 菜农李伟种植的某蔬菜计划以5元/千克的单价对外批发销售，由于部分菜农盲目扩大种植，造成蔬菜滞销，李伟为了加快销售，减少损失，对价格进行两次下调后，以3.2元/千克的单价对外批发销售。
    (1)、求平均每次下调的百分率。
    (2)、如果李伟按以前的调价方案再进行一次调价，蔬菜的批发价会跌破2.5元/千克吗？

    查看试题解析