浙教版数学九上第1章 二次函数 三阶单元测试卷
试卷更新日期:2024-07-24 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 已知点A(x1 , y1)在抛物线y1=nx2﹣2nx+n上,点B(x2 , y2)在直线y2=﹣nx+n,当n>0时,下列判断正确的是( )A、当x1=x2<1时,y1<y2 B、当x1=x2>1时,y1<y2 C、当y1=y2>n时,x1>x2 D、当y1=y2<n时,x1>x22. 定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min(﹣x2+3,﹣2x}的最大值是( )A、3 B、2 C、1 D、03. 据科学计算,运载“神十八”的“长征二号”火箭,在点火第一秒钟通过的路程为 , 第二秒时共通过了的路程,第三秒时共通过了的路程,在这一过程中路程与时间成二次函数关系,在达到离地面的高度时,火箭程序拐弯,则这一过程需要的时间大约是( ).
 A、10秒钟 B、13秒钟 C、15秒钟 D、20秒钟4. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
A、10秒钟 B、13秒钟 C、15秒钟 D、20秒钟4. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )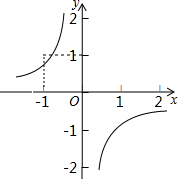 A、
A、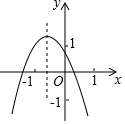 B、
B、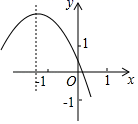 C、
C、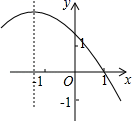 D、
D、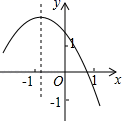 5. 在平面直角坐标系中,二次函数()的图象与x轴的一个交点的横坐标为 , 则另一个交点的横坐标为( )A、5 B、3 C、 D、6. 已知点 , 都在抛物线上,若当时,都有 , 则实数k的取值范围是( )A、 B、 C、 D、或7. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限8. 如图,四边形为菱形,为上一点,的垂直平分线交于点F , 若 , 记的面积最大值为S , 周长最小值为l , 则( )
5. 在平面直角坐标系中,二次函数()的图象与x轴的一个交点的横坐标为 , 则另一个交点的横坐标为( )A、5 B、3 C、 D、6. 已知点 , 都在抛物线上,若当时,都有 , 则实数k的取值范围是( )A、 B、 C、 D、或7. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限8. 如图,四边形为菱形,为上一点,的垂直平分线交于点F , 若 , 记的面积最大值为S , 周长最小值为l , 则( ) A、 B、 C、 D、9. 关于一元二次方程有以下命题:①若a+b+c=0,则(≥0;②若方程(的两根为-1和2,则2a+c=0;③若方程(有两个不相等的实数根,则方程=0必有两个不相等的实数根;④若方程 有两个相等的实数根,则 无实数根.其中真命题是( )A、①② B、①②③ C、②③④ D、①③④10. 如图,是二次函数图象的一部分,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若 , 为函数图象上的两点,则 . 其中正确的结论有
A、 B、 C、 D、9. 关于一元二次方程有以下命题:①若a+b+c=0,则(≥0;②若方程(的两根为-1和2,则2a+c=0;③若方程(有两个不相等的实数根,则方程=0必有两个不相等的实数根;④若方程 有两个相等的实数根,则 无实数根.其中真命题是( )A、①② B、①②③ C、②③④ D、①③④10. 如图,是二次函数图象的一部分,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若 , 为函数图象上的两点,则 . 其中正确的结论有 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本题有6小题,每小题4分,共24分)
-
11. 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系的图象,点在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长 , 高的矩形,则可判定货车完全停到车棚内(填“能”或“不能”).
 12. 如图,平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣ x2 , 桥下的水面宽AB为6m,当水位上涨2m时,水面宽CD为m(结果保留根号).
12. 如图,平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣ x2 , 桥下的水面宽AB为6m,当水位上涨2m时,水面宽CD为m(结果保留根号). 13. 从地面竖直向上抛出一个小球,若小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系满足 , 则小球从抛出到落地共用时s.14. 如图,抛物线的图象与x轴交于点A , 与y轴交于点B , 且 .
13. 从地面竖直向上抛出一个小球,若小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系满足 , 则小球从抛出到落地共用时s.14. 如图,抛物线的图象与x轴交于点A , 与y轴交于点B , 且 . (1)、 .(2)、已知点P为该抛物线上一点且设其横坐标为 , 记该抛物线在点B与点P之间(包含点B和点P)这部分图象的最高点和最低点到x轴的距离分别为 . 若 , 则t的取值范围为 .15. 图1是一个瓷碗,图 2 是其截面图,碗体 DEC 呈抛物线状(碗体厚度不计),碗口宽CD=12cm,此时面汤最大深度EG=8cm.
(1)、 .(2)、已知点P为该抛物线上一点且设其横坐标为 , 记该抛物线在点B与点P之间(包含点B和点P)这部分图象的最高点和最低点到x轴的距离分别为 . 若 , 则t的取值范围为 .15. 图1是一个瓷碗,图 2 是其截面图,碗体 DEC 呈抛物线状(碗体厚度不计),碗口宽CD=12cm,此时面汤最大深度EG=8cm. (1)、当面汤的深度ET为4cm时,汤面的直径PQ长为;(2)、如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当∠ABM=45°时停止,此时碗中液面宽度CH= .16. 抛物线( , 是常数且 , )经过点 . 下列四个结论:①该抛物线一定经过;②;③点 , 在抛物线上,且 , 则④若 , 是方程的两个根,其中 , 则 . 其中正确的结论是(填写序号).
(1)、当面汤的深度ET为4cm时,汤面的直径PQ长为;(2)、如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当∠ABM=45°时停止,此时碗中液面宽度CH= .16. 抛物线( , 是常数且 , )经过点 . 下列四个结论:①该抛物线一定经过;②;③点 , 在抛物线上,且 , 则④若 , 是方程的两个根,其中 , 则 . 其中正确的结论是(填写序号).三、解答题(本题共8小题,第17题9分,第18题9分,第19题6分,第20题9分,第21题9分,第22题4分,第23题10分,第24题10分,共66分)
-
17. 已知,关于的二次函数 .(1)、若函数经过点 , 求拋物线的对称轴.(2)、若点P(t-2,p),Q(t+3,q)均在抛物钱y=2x2-4tx-3上,则pq(填">",“<"或"=”).(3)、记 , 当时,始终成立,求的取值范围.18. 已知二次函数的图象L过点 , 顶点坐标为 .(1)、求这个二次函数的表达式;(2)、L与x轴相交于A , B两点(点A在点B左侧),求A , B两点坐标;(3)、将L向上平移个单位长度,与x轴相交于 , 两点,若点在线段上,求k的取值范围.19. 已知二次函数(为常数且)的顶点在轴上方,且到轴的距离为4.
 (1)、求二次函数的解析式;(2)、将二次函数的图象记为 , 将关于原点对称的图象记为与合起来得到的图象记为 , 完成以下问题:
(1)、求二次函数的解析式;(2)、将二次函数的图象记为 , 将关于原点对称的图象记为与合起来得到的图象记为 , 完成以下问题:①在网格中画出函数的图象;
②若对于函数上的两点 , 当时,总有 , 求出的取值范围.
20. 某商品每件进价25元,在试销阶段该商品的日销售量y(件)与每件商品的日销售价x(元)之间的关系如图中的折线ABC所示(物价局规定,该商品每件的销售价不得低于进价且不得高于50元). (1)、直接写出y与x的函数关系式;(2)、若日销售单价x(元)为整数 , 则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;(3)、若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.21. 【项目式学习】
(1)、直接写出y与x的函数关系式;(2)、若日销售单价x(元)为整数 , 则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;(3)、若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.21. 【项目式学习】项目主题:如何拟定运动员拍照记录的方案?
项目背景:
(1)、任务一:确定滑道的形状图1是单板滑雪运动员从大跳台滑雪场地滑出的场景,图2是跳台滑雪场地的横截面示意图.AC垂直于水平底面BC,点D到A之间的滑道呈抛物线型,已知m,m,且点B处于跳台滑道的最低处,在图2中建立适当的平面直角坐标系,求滑道所在抛物线的函数表达式.
 (2)、任务二:确定运动员达到最高点的位置
(2)、任务二:确定运动员达到最高点的位置如图3,某运动员从点A滑出后的路径满足以下条件:
①运动员滑出路径与D、A之间的抛物线形状相同 ,
②该运动员在底面BC上方竖直距离9.75m处达到最高点P
③落点Q在底面BC下方竖直距离2.25m.
在同一平面直角坐标系中,求运动员到达最高处时与点A的水平距离.
(3)、任务三:确定拍摄俯角高速摄像机能高度还原运动员的精彩瞬间,如图4,有一台摄像机M进行跟踪拍摄:
①它与点B位于同一高度,且与点B距离25.5m;
②运动过程需在摄像头视角范围内才能记录,记摄像头的俯角为;
③在平面直角坐标系中,设射线MN的解析式为 , 其比例系数k和俯角的函数关系如图5所示.
若要求运动员的落点Q必须在摄像机M的视角范围内,则俯角至少多少度(精确到个位)?
 22.
22.草莓种植大棚的设计
生活背景
草莓种植大棚是一种具有保温性能的框架结构.如图示,一般使用钢结构作为骨架,上面覆上一层或多层塑料膜,这样就形成了一个温室空间.大棚的设计要保证通风性且利于采光.

建立模型
如图1,已知某草莓园的种植大棚横截面可以看作抛物线 , 其中点P为抛物线的顶点,大棚高 , 宽 . 现以点O为坐标原点,所在直线为x轴,过点O且垂直于的直线为y轴建立平面直角坐标系.求此抛物线的解析式.

图1
解决问题
如图2,为方便进出,在大棚横截面中间开了两扇正方形的门,其中 . 求门高的值.
若在某一时刻,太阳光线(假设太阳光线为平行线)透过A点恰好照射到N点,此时大棚横截面在地面上的阴影为线段 , 求此时的长.

图2
23. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .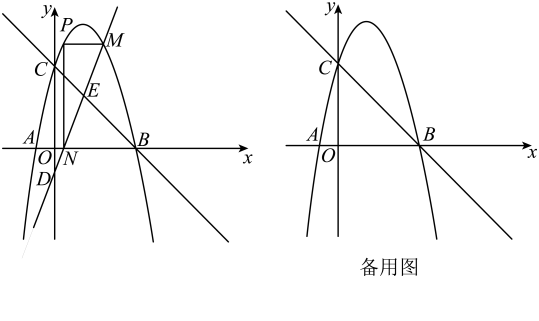 (1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.24. 如图,抛物线经过、两点,为抛物线上第一象限内的一个动点.
(1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.24. 如图,抛物线经过、两点,为抛物线上第一象限内的一个动点. (1)、求抛物线所对应的函数表达式;(2)、当的面积最大时,求点的坐标;(3)、过点作 , 垂足为点 , 是否存在点 , 使 , 若存在,求点的横坐标;若不存在,请说明理由.
(1)、求抛物线所对应的函数表达式;(2)、当的面积最大时,求点的坐标;(3)、过点作 , 垂足为点 , 是否存在点 , 使 , 若存在,求点的横坐标;若不存在,请说明理由.