浙教版数学九上章末重难点专训二次函数的与不等式（组）、一元二次方程、一次函数的综合运用

试卷更新日期：2024-07-24 类型：单元试卷

进入出卷网下载

一、选择题

1. 如下表中列出了二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的一些对应值，则一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的其中一个近似解 $x_{1}$ 的范围是（）
x
…
$- 3$
$- 2$
$- 1$
0
1
…
y
…
$- 11$
$- 5$
$- 1$
1
1
…

A、 $- 3 ＜ x_{1} ＜ - 2$ B、 $- 2 ＜ x_{1} ＜ - 1$ C、 $- 1 ＜ x_{1} ＜ 0$ D、 $0 ＜ x_{1} ＜ 1$

查看试题解析
2. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）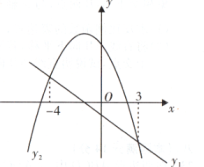

A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析
3. 如图，抛物线y₁＝ax²+bx+c与直线y₂＝mx+n相交于点（3，0）和（0，3），若ax²+bx+c＞mx+n，则x的取值范围是（）

A、0＜x＜3 B、1＜x＜3 C、x＜0或x＞3 D、x＜1减x＞3

查看试题解析
4. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = 1$ ，与x轴的一个交点坐标为 $(- 1, 0)$ ，其部分图象如图所示，其中结论不正确的是（）．

A、 $4 a c < b^{2}$ B、方程 $a x^{2} + b x + c = 0$ 的两个根是 $x_{1} = - 1$ ， $x_{2} = 3$ C、 $3 a + c > 0$ D、当 $x < 0$ 时，y随x增大而增大

查看试题解析
5. 已知 $m > n > 0$ ，若关于x的方程 $x^{2} + 2 x - 3 - m = 0$ 的解为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ．关于x的方程 $x^{2} + 2 x - 3 - n = 0$ 的解为 $x_{3} ， x_{4} (x_{3} < x_{4})$ ．则下列结论正确的是（）

A、 $x_{3} < x_{1} < x_{2} < x_{4}$ B、 $x_{1} < x_{3} < x_{4} < x_{2}$ C、 $x_{1} < x_{2} < x_{3} < x_{4}$ D、 $x_{3} < x_{4} < x_{1} < x_{2}$

查看试题解析
6. 已知ac≠0，若二次函数y₁＝ax²+bx+c的图象与x轴交于两个不同的点A（x₁ ， 0），B（x₂ ， 0），二次函数y₂＝cx²+bx+a的图象与x轴交于两个不同的点C（x₃ ， 0），D（x₄ ， 0），则（　　）

A、x₁+x₂+x₃+x₄＝1 B、x₁x₂x₃x₄＝1 C、 $\frac{x_{1} + x_{2}}{x_{3} + x_{4}} = 1$ D、 $\frac{x_{1} x_{2}}{x_{3} x_{4}} = 1$

查看试题解析
7. 如图是二次函数 $y_{1} = a x^{2} + b x + c$ 和一次函数 $y_{2} = k x + t$ 的图象，当 $y_{1} < y_{2}$ 时，x的取值范围是（）

A、 $x < - 1$ B、 $x > 2$ C、 $- 1 < x < 2$ D、 $x < - 1$ 或 $x > 2$

查看试题解析
8. 设函数 $y_{1} = x^{2} + b x + c$ 的图象与 $x$ 轴交点的横坐标分别为 $α_{1}$ ， $β_{1}$ ，函数 $y_{2} = x^{2} + d x + e$ 的图象与 $x$ 轴交点的横坐标分别为 $α_{2}$ ， $β_{2}$ .当 $x = α_{2}$ 和 $β_{2}$ 时，函数 $y_{1}$ 的值分别为 $A_{1}$ ， $B_{1}$ ；当 $x = α_{1}$ 和 $β_{1}$ 时，函数 $y_{2}$ 的值分别为 $A_{2}$ ， $B_{2}$ ，则（）

A、 $A_{1} B_{1} = A_{2} B_{2}$ B、 $A_{1} + B_{1} = A_{2} + B_{2}$ C、 $A_{1} B_{2} = A_{2} B_{1}$ D、 $A_{1} + B_{2} = A_{2} + B_{1}$

查看试题解析
9. 如图，抛物线 $y = x^{2} - b x + c$ 与x轴交于C、D两点（点C在点D的左侧），顶点在线段 $A B$ 上运动， $A B / / x$ 轴， $B (1 ， - 1)$ ， $A B = 3$ ，则下列结论中正确的是（）

A、 $b^{2} - 4 c < 0$ B、当 $x > 0$ 时，一定有y随x的增大而增大 C、 $0 \leq c \leq 3$ D、若点C的坐标为 $(m ， 0)$ ，则点D的坐标为 $(m + 2 ， 0)$

查看试题解析

二、填空题

10. 二次函数 $y = a x^{2} + b x$ 的图象如图，若一元二次方程 $a x^{2} + b x = m$ 有实数根，则 $m$ 的最小值为

查看试题解析
11. 如图，已知抛物线 $y = a x^{2} + b x + c$ 与直线 $y = k x + m$ 交于 $A (- 3 ， - 1) ， B (0 ， 2)$ 两点，则关于x的不等式 $a x^{2} + b x + c > k x + m$ 的解集是．

查看试题解析
12. 若抛物线 $y = m x^{2} - 6 x - 9$ 与x轴只有一个交点，则m的值为.

查看试题解析
13. 二次函数 $y = a x^{2} + b x$ 的图象如图所示，若关于x的一元二次方程 $a x^{2} + b x = m$ 有实数根，则m的值可以为（写出一个值即可）

查看试题解析
14. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是直线 $x = - 1$ ，经过点 $(- 3, 0)$ ，且 $b > 0$ ．下列结论：
① $c < 0$ ；
② $a + b + c = 0$ ；
③若 $(x_{1}, y_{1})$ 和 $(x_{2}, y_{2})$ 是抛物线上的两点，则当 $| x_{1} + 1 | > | x_{2} + 1 |$ 时， $y_{1} < y_{2}$ ；
④若抛物线的顶点坐标为 $(- 1, m)$ ，则关于的方程 $a x^{2} + b x + c = m - 1$ 无实数根其中正确的结论是（填写序号）．

查看试题解析
15. 若关于x的方程 $| x^{2} - 4 x + 3 | = x + t$ 恰有三个根，则t的值为.

查看试题解析
16. 如图，直线y= $\frac{1}{2}$ x+2与y轴交于点A，与直线y= $- \frac{1}{2}$ x交于点B．以AB为边向右作菱形ABCD，点C恰好与原点O重合．抛物线y=(x-h)²+k的顶点在直线y= $- \frac{1}{2}$ x上移动．若抛物线与菱形的边AB，BC都有公共点，则h的取值范围是

查看试题解析

三、解答题

17. 如图，二次函数y＝ax² $- \frac{4}{3} x + c$ 的图象与x轴交于点A（3，0），与y轴交于点B（0，-2）.

(1)、求二次函数的解析式；

(2)、若点P为抛物线上一动点（直线AB上方），且S△PBA＝4，求点P的坐标.

查看试题解析
18. 已知抛物线 $y = (m - 2) x^{2} - 2 m x + m + 2$ .

(1)、当 $m = 1$ 时，求该抛物线的对称轴；

(2)、当该抛物线与 $x$ 轴两交点的横坐标都为正整数时，求整数 $m$ 的值.

查看试题解析
19. “五一”前夕，某超市销售一款商品，进价每件75元，售价每件140元，每天销售40件，每销售一件需支付给超市管理费5元．从五月一日开始，该超市对这款商品开展为期一个月“每天降价1元”的促销活动，即从第一天（5月1日）开始每天的售价均比前一天降低1元．通过市场调查发现，该商品的日销售量y（件）与第x天（ $1 \leq x \leq 31$ ，且x为整数）之间存在一次函数关系，x ， y之间的部分数值对应关系如下表：
第x天
5
10
15
20
日销售量y（件）
50
60
70
80

(1)、直接写出y与x的函数关系式；

(2)、设第x天的利润为W元，试求出W与x之间的函数关系式，并求出哪一天的利润最大？最大利润是多少元？

(3)、销售20天后，由于某种原因，该商品的进价从第21天开始每件下降4元，其他条件保持不变，求超市在这一个月中，该商品的日销售利润不低于3430元的共有多少天？

查看试题解析
20. 已知抛物线 $y = \frac{1}{2} x^{2} - m x + m^{2}$ 经过点 $P (2 ， k)$ .请解决下列问题：

(1)、点 $A (a ， n) ， B (b ， n)$ 分别落在抛物线 $y = \frac{1}{2} x^{2} - m x + m^{2}$ 上，且 $a + b = 4$ ，求 $k$ 的值.

(2)、当 $- 2 ⩽ m ⩽ 1$ 时，
①求 $k$ 的取值范围.
②若 $- 2 ⩽ x ⩽ 1 ， y_{最大} - y_{最小} = 4$ ，求 $m$ 的值.

查看试题解析

四、实践探究题

21. 如图，是某公园的一种水上娱乐项目.数学兴趣小组对该项目中的数学问题进行了深入研究.下面是该小组绘制的水滑道截面图，如图1，人从点A处沿水滑道下滑至点B处腾空飞出后落入水池.以地面所在的水平线为x轴，过腾空点B与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系.他们把水滑道和人腾空飞出后经过的路径都近似看作是抛物线的一部分.根据测量和调查得到的数据和信息，设计了以下三个问题，请你解决.

(1)、如图1，点B与地面的距离为2米，水滑道最低点C与地面的距离为 $\frac{7}{8}$ 米，点C到点B的水平距离为3米，则水滑道 $A C B$ 所在抛物线的解析式为；

(2)、如图1，腾空点B与对面水池边缘的水平距离 $O E = 12$ 米，人腾空后的落点D与水池边缘的安全距离 $D E$ 不少于3米.若某人腾空后的路径形成的抛物线 $B D$ 恰好与抛物线 $A C B$ 关于点B成中心对称.
①请直接写出此人腾空后的最大高度和抛物线 $B D$ 的解析式；
②此人腾空飞出后的落点D是否在安全范围内？请说明理由（水面与地面之间的高度差忽略不计）；

(3)、为消除安全隐患，公园计划对水滑道进行加固.如图2，水滑道已经有两条加固钢架，一条是水滑道距地面4米的点M处竖直支撑的钢架 $M N$ ，另一条是点M与点B之间连接支撑的钢架 $B M$ .现在需要在水滑道下方加固一条支撑钢架，为了美观，要求这条钢架与 $B M$ 平行，且与水滑道有唯一公共点，一端固定在钢架 $M N$ 上，另一端固定在地面上.请你计算出这条钢架的长度（结果保留根号）.

查看试题解析
22. 定义：在平面直角坐标系中，设直线 $l$ 的解析式为： $y = k x + m$ ( $k 、 m$ 为常数且 $k \neq 0$ )，当直线 $l$ 与一条曲线有且只有一个公共点时，我们称直线 $l$ 与这条曲线“相切”，这个公共点叫做“切点”．根据定义，完成下列问题．

(1)、求直线 $l$ ： $y = - x + 6$ 与曲线 $y = \frac{9}{x}$ 的切点坐标；

(2)、已知函数 $y_{1} = 2 x$ ，函数 $y_{2} = x^{2} + 1$ ，是否存在二次函数 $y_{3} = a x^{2} + b x + c$ ，其图象过点 $(- 3 ， 2)$ ，使得直线 $y_{1} = 2 x$ 与曲线 $y_{2}, y_{3}$ 都相切于同一点?若存在，求出 $y_{3}$ 的解析式若不存在，请说明理由；

(3)、已知直线 $l_{1} : y_{1} = k_{1} x + m_{1} (k_{1} \neq 0)$ ，直线 $l_{2} : y_{2} = k_{2} x + m_{2} (k_{2} \neq 0)$ 是抛物线 $y = - x^{2} + 2 x + 2$ 的两条切线，当 $l_{1}$ 与 $l_{2}$ 的交点 $P$ 的纵坐标为4时，试判断 $k_{1} \cdot k_{2}$ 是否为定值，并说明理由．

查看试题解析
23. 规定[n， n-3， --3](n为正整数)为二次函数 $y ₙ = n x^{2} + (n - 3) x - 3$ 的“函系数”，
如：当n=1时， $y_{1} = x^{2} - 2 x - 3$ 的“函系数”为[1， --2， --3]；
当n = 2 时， $y_{2} = 2 x^{2} - x - 3$ 的“函系数”为[2， --1， --3]；
设二次函数yn与x轴的交点分别为An，Bn(点An在Bn的左边) .

(1)、当n=5时，对应的二次函数的解析式为；

(2)、求点An， Bn的坐标(用含 n的式子表示) .

(3)、当n≥4时，二次函数 $y ₙ = n x^{2} + (n - 3) x - 3$ 与直线y=-3的一个交点为( $C ₙ$ (点Cn不在y轴上).判断线段 $B ₙ B ₙ_{+}_{1}$ 和线段( $C ₙ C ₙ_{+}_{1}$ 的数量关系，并说明理由.

查看试题解析

五、综合题

24. 已知抛物线 $G : y = a x^{2} - 6 a x - a^{3} + 2 a^{2} + 1 (a > 0)$ 过点 $A (x_{1}, 2)$ 和点 $B (x_{2}, 2)$ ，直线 $l : y = m^{2} x + n$ 过点 $C (3, 1)$ ，交线段 $A B$ 于点 $D$ ，记 $△ C D A$ 的周长为 $C_{1}$ ， $△ C D B$ 的周长为 $C_{2}$ ，且 $C_{1} = C_{2} + 2$ ．

(1)、求抛物线 $G$ 的对称轴；

(2)、求 $m$ 的值；

(3)、直线 $l$ 绕点 $C$ 以每秒 $3 °$ 的速度顺时针旋转 $t$ 秒后 $(0 \leq t < 45)$ 得到直线 $l^{'}$ ，当 $l^{'} ∥ A B$ 时，直线 $l^{'}$ 交抛物线 $G$ 于 $E$ ， $F$ 两点．
①求 $t$ 的值；
②设 $△ A E F$ 的面积为 $S$ ，若对于任意的 $a > 0$ ，均有 $S \geq k$ 成立，求 $k$ 的最大值及此时抛物线 $G$ 的解析式．

查看试题解析
25. 已知：抛物线 $C_{1}$ ： $y = a x^{2} + b x + c (a > 0)$ .

(1)、若顶点坐标为 $(1, 1)$ ，求b和c的值（用含a的代数式表示）；

(2)、当 $c < 0$ 时，求函数 $y = - 2024 | a x^{2} + b x + c | - 1$ 的最大值；

(3)、若不论m为任何实数，直线 $y = m (x - 1) - \frac{m^{2}}{4}$ 与抛物线 $C_{1}$ 有且只有一个公共点，求a ， b ， c的值；此时，若 $k \leq x \leq k + 1$ 时，抛物线的最小值为k ，求k的值.

查看试题解析
26. 春回大地，万物复苏，又是一年花季到.某花圃基地计划将如图所示的一块长40 m，宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区，另一块空地为活动区，其余空地为种植区，分别种植A，B，C三种花卉.活动区一边与育苗区等宽，另一边长是10 m.A，B，C三种花卉每平方米的产值分别是2百元、3百元、4百元.

(1)、设育苗区的边长为x m，用含x的代数式表示下列各量：花卉A的种植面积是 $m^{2}$ ，花卉B的种植面积是 $m^{2}$ ，花卉C的种植面积是 $m^{2}$ .

(2)、育苗区的边长为多少时，A，B两种花卉的总产值相等？

(3)、若花卉A与B的种植面积之和不超过 $560 m^{2}$ ，求A，B，C三种花卉的总产值之和的最大值.

查看试题解析
27. 如图，直线l： $y = \frac{2}{3} x - 1$ 与反比例函数 $y = \frac{k}{x}$ 相交于A ， B两点过点A作AC⊥x轴，垂足为点C ，且AC =1．

(1)、求反比例函数 $y = \frac{k}{x}$ 的解折式；

(2)、求出B点的坐标，并直接写出不等式 $\frac{2}{3} x - \frac{k}{x} > 1$ 的解集．

查看试题解析
28. 设一次函数y₁＝a（x+m）的图象与x轴交于点A ，二次函数 $y_{2} = a x^{2} + b x + c$ 的图象与x轴交于A，B两个不同的点，设函数y=y₁+y₂ ．

(1)、设点Q（0，q）在函数y的图象上，若q＞c，求证：am＞0．

(2)、若函数y₂ ， y的图象在x轴上截得的线段长分别为d₁ ， d₂ ，求d₁ ， d₂的数量关系式．

(3)、若函数y₁的图象分别与函数y₂的图象、函数y的图象交于点E（x₁ ， e），F（x₂ ， f），且点E，F不同于点A，求x₁-x₂的值．

查看试题解析
29. 如图，在平面直角坐标系中，二次函数 $y = - x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A ， B$ 两点，与 $y$ 轴交于点 $C (0 ， 3)$ ，点A在原点的左侧，点 $B$ 的坐标为 $(3 ， 0)$ ，点 $P$ 是抛物线上一个动点，且在直线 $B C$ 的上方．

(1)、求这个二次函数的解析式；

(2)、当点 $P$ 运动到什么位置时， $△ B P C$ 的面积最大？请求出点 $P$ 的坐标和 $△ B P C$ 面积的最大值．

(3)、连接 $P O ， P C$ ，并把 $△ P O C$ 沿 $C O$ 翻折，得到四边形 $P O P^{'} C$ ，那么是否存在点 $P$ ，使四边形 $P O P^{'} C$ 为菱形？若存在，请求出此时点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析

x	…	$- 3$	$- 2$	$- 1$	0	1	…
y	…	$- 11$	$- 5$	$- 1$	1	1	…

第x天	5	10	15	20
日销售量y（件）	50	60	70	80

浙教版数学九上章末重难点专训 二次函数的与不等式（组）、一元二次方程、一次函数的综合运用

一、选择题

二、填空题

三、解答题

四、实践探究题

五、综合题

浙教版数学九上章末重难点专训二次函数的与不等式（组）、一元二次方程、一次函数的综合运用