浙教版数学九上章末重难点专训 二次函数的图象与字母系数之间的关系(选填)
试卷更新日期:2024-07-24 类型:单元试卷
一、选择题
-
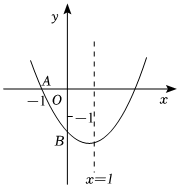
1. 如图是二次函数 图象的一部分,其对称轴为. 且过点()有下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若是抛物线上两点,则.其中说法正确的是( )
 A、①② B、②③ C、①②④ D、②③④2. 函数y=|ax2+bx+c|(a>0,b2-4ac>0)的图象是由函数y=ax2+bx+c(a>0,b2-4ac>0)的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论:①2a+b=0;②c=3;③abc>0;④将图象向上平移1个单位长度后与直线y=5有3个交点.其中正确的是( )
A、①② B、②③ C、①②④ D、②③④2. 函数y=|ax2+bx+c|(a>0,b2-4ac>0)的图象是由函数y=ax2+bx+c(a>0,b2-4ac>0)的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论:①2a+b=0;②c=3;③abc>0;④将图象向上平移1个单位长度后与直线y=5有3个交点.其中正确的是( ) A、①② B、①③ C、②③④ D、①③④3. 如图,抛物线与x轴交于A , B两点,与y轴交于点 , 点A在与之间(不包含这两点),抛物线的顶点为D , 对称轴是直线 . 有下列结论:①;②若点;是抛物线上两点,则;③;④若 , 则是等边三角形.其中正确的个数是( )
A、①② B、①③ C、②③④ D、①③④3. 如图,抛物线与x轴交于A , B两点,与y轴交于点 , 点A在与之间(不包含这两点),抛物线的顶点为D , 对称轴是直线 . 有下列结论:①;②若点;是抛物线上两点,则;③;④若 , 则是等边三角形.其中正确的个数是( ) A、1 B、2 C、3 D、44. 抛物线交轴于 , , 交轴的负半轴于 , 顶点为 . 下列结论:①;②;③当时,;④当是等腰直角三角形时,则;⑤若 , 是一元二次方程的两个根,且 , 则 . 其中正确的有( )个
A、1 B、2 C、3 D、44. 抛物线交轴于 , , 交轴的负半轴于 , 顶点为 . 下列结论:①;②;③当时,;④当是等腰直角三角形时,则;⑤若 , 是一元二次方程的两个根,且 , 则 . 其中正确的有( )个 A、2 B、3 C、4 D、55. 已知二次函数的图象如图所示,顶点为(﹣1,0),则下列结论:
A、2 B、3 C、4 D、55. 已知二次函数的图象如图所示,顶点为(﹣1,0),则下列结论:①;②;③;④;⑤ .
其中正确结论的个数是( )
 A、2个 B、3个 C、4个 D、5个6. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
A、2个 B、3个 C、4个 D、5个6. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0④当y>0时,x的取值范围是-1≤x<3⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
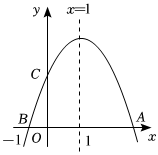
 A、4个 B、3个 C、2个 D、1个7. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图象如图所示,给出以下判断:(1);(2);(3);(4)直线与抛物线两个交点的横坐标分别为 , , 则 , 其中正确的有( )
A、4个 B、3个 C、2个 D、1个7. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图象如图所示,给出以下判断:(1);(2);(3);(4)直线与抛物线两个交点的横坐标分别为 , , 则 , 其中正确的有( ) A、4个 B、3个 C、2个 D、1个8. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
A、4个 B、3个 C、2个 D、1个8. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )① ;②;③;④将图象向上平移1个单位后与直线有3个交点.
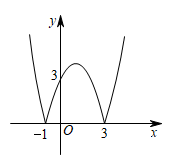 A、①② B、①③ C、②③④ D、①③④9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①abc<0;②方程:ax2+bx+c=0(3≠0)必有一个根大于2且小于3;③若 , 是抛物线上的两点,那么y1<y2;④11a+2c>0;⑤对于任意实数m , 都有m(am+b)≥a+b , 其中正确结论的是( )
A、①② B、①③ C、②③④ D、①③④9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①abc<0;②方程:ax2+bx+c=0(3≠0)必有一个根大于2且小于3;③若 , 是抛物线上的两点,那么y1<y2;④11a+2c>0;⑤对于任意实数m , 都有m(am+b)≥a+b , 其中正确结论的是( ) A、②④ B、①②④ C、②④⑤ D、②③④10. 如图,抛物线与轴交于、两点,与轴交于点 , 且 , 是抛物线的顶点,三角形的面积等于1,则以下结论:①;②;③;④ , 其中正确的结论是( )
A、②④ B、①②④ C、②④⑤ D、②③④10. 如图,抛物线与轴交于、两点,与轴交于点 , 且 , 是抛物线的顶点,三角形的面积等于1,则以下结论:①;②;③;④ , 其中正确的结论是( ) A、②④ B、①②④ C、①③④ D、①②③④11. 如图是二次函数(a , b , c是常数,)图象的一部分,与x轴的交点在点和之间,对称轴是 . 对于下列说法:①;②;③当时,;④ . 其中正确的个数是( )
A、②④ B、①②④ C、①③④ D、①②③④11. 如图是二次函数(a , b , c是常数,)图象的一部分,与x轴的交点在点和之间,对称轴是 . 对于下列说法:①;②;③当时,;④ . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个12. 如图,二次函数的图象经过点 , 对称轴为直线 , 下列结论:(1)0;(2);(3);(4)若两点在该二次函数的图象上,则 . 其中正确的有( )
A、1个 B、2个 C、3个 D、4个12. 如图,二次函数的图象经过点 , 对称轴为直线 , 下列结论:(1)0;(2);(3);(4)若两点在该二次函数的图象上,则 . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个13. 如图,抛物线的对称轴为x=-1,且过点( , 有下列结论:①abc>0; ②a-2b+4c>0; ③25a-10b+4c=0; ④3b+2c>0;其中正确的结论的个数是( )
A、1个 B、2个 C、3个 D、4个13. 如图,抛物线的对称轴为x=-1,且过点( , 有下列结论:①abc>0; ②a-2b+4c>0; ③25a-10b+4c=0; ④3b+2c>0;其中正确的结论的个数是( ) A、1 B、2 C、3 D、414. 如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0;②a+b>0;③0<a<-c;④若点C( , y1),D( , y2)在抛物线上,则y1>y2其中,正确的结论有( )个
A、1 B、2 C、3 D、414. 如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0;②a+b>0;③0<a<-c;④若点C( , y1),D( , y2)在抛物线上,则y1>y2其中,正确的结论有( )个 A、4 B、3 C、2 D、115. 函数的图象是由函数的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是( )
A、4 B、3 C、2 D、115. 函数的图象是由函数的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是( )①;②;③;④将图象向上平移2个单位后与直线有3个交点.
 A、①② B、①③④ C、②③④ D、①③
A、①② B、①③④ C、②③④ D、①③二、填空题
-
16. 已知二次函数图象如图所示,有下列4个结论:①;②;③;④;其中正确的结论 .
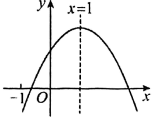 17. 二次函数y=ax²+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc﹤0;②3a+c﹥0;③(a+c)2-b2﹤0;④a+b≤m(am+b)(m为实数).其中正确的结论有.
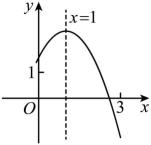
17. 二次函数y=ax²+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc﹤0;②3a+c﹥0;③(a+c)2-b2﹤0;④a+b≤m(am+b)(m为实数).其中正确的结论有.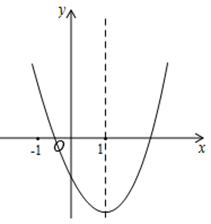 18. 如图是二次函数的图象,下列结论:
18. 如图是二次函数的图象,下列结论:①二次三项式的最大值为4;
②4a+2b+c<0;
③一元二次方程的两根之和为-1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的有(填序号).
 19. 如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间不包括这两点 , 对称轴为直线下列结论:;;;;其中正确结论有填写所有正确结论的序号 .
19. 如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间不包括这两点 , 对称轴为直线下列结论:;;;;其中正确结论有填写所有正确结论的序号 .