【培优版】2024-2025学年浙教版数学九上1.3二次函数的性质 同步练习
试卷更新日期:2024-07-24 类型:同步测试
一、选择题
-
1. 抛物线y=﹣x2+bx+c与x轴交于两点,其中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正确的是( )A、b+c>1 B、b=2 C、b2+4c<0 D、c<02. 已知二次函数y=ax2+bx+c(a≠0),当y<n时,x的取值范围是t-3<x<1-t , 且该二次函数的图象经过点M(3,m2+3),N(d , 2m)两点,则d的值不可能是( )A、-3 B、-1 C、2 D、43. 如图所示,抛物线经过矩形ABCD的三个顶点A , B , D,则点C的坐标为( )
 A、 B、 C、 D、4. 已知二次函数的图象经过点 , , . 当时,该函数有最大值和最小值 , 则( )A、有最大值 B、无最大值 C、有最小值 D、无最小值5. 设一元二次方程 的两根分别为 ,且 ,则
A、 B、 C、 D、4. 已知二次函数的图象经过点 , , . 当时,该函数有最大值和最小值 , 则( )A、有最大值 B、无最大值 C、有最小值 D、无最小值5. 设一元二次方程 的两根分别为 ,且 ,则满足( )
A、 B、 C、 D、 且6. 如图,抛物线与x轴交于点A(-6,0).点 , 是抛物线上两点,当t≤x≤t+3时,二次函数最大值记为 , 最小值记为 , 设 , 则m的取值范围是( )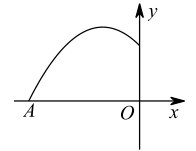 A、 B、 C、 D、7. 如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )
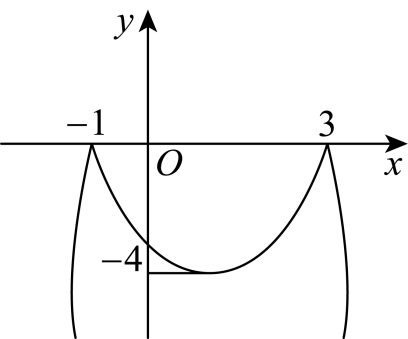
A、 B、 C、 D、7. 如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )①图象具有对称性,对称轴是直线; ②由图象得 , , ;③该“陷阱”函数与y轴交点坐标为;④的“陷阱”函数与的“陷阱”函数的图象是完全相同的.
 A、1 B、2 C、3 D、48. 二次函数的顶点坐标为 , 其部分图象如图所示,下列结论:①;②③若点 , 点是函数图象上的两点,则;④关于x的方程无实数根;其中正确结论有( )
A、1 B、2 C、3 D、48. 二次函数的顶点坐标为 , 其部分图象如图所示,下列结论:①;②③若点 , 点是函数图象上的两点,则;④关于x的方程无实数根;其中正确结论有( )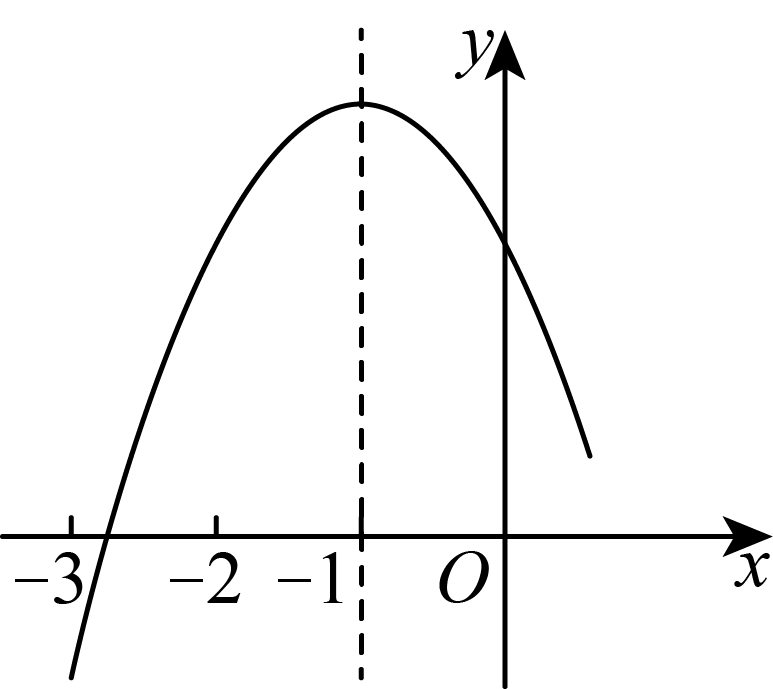 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 已知二次函数(m为常数)的图象与x轴有交点,且当x<-3时,y随x的增大而增大,则m的取值范围是10. 如图,在纸片中, , , , 点 , 分别在、边上,连接 , 将沿翻折,使点落在点的位置,且四边形是菱形.
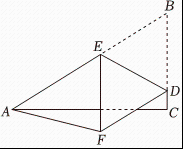 (1)、若点在边上时,则菱形的边长为;(2)、连接 , 则的长的最小值为 .11. 如图,在正方形ABCD中, , 点E为对角线AC上的动点,以DE为边作正方形DEFG.点H是CD上一点,且 , 连接GH,则GH的最小值为 .
(1)、若点在边上时,则菱形的边长为;(2)、连接 , 则的长的最小值为 .11. 如图,在正方形ABCD中, , 点E为对角线AC上的动点,以DE为边作正方形DEFG.点H是CD上一点,且 , 连接GH,则GH的最小值为 . 12. 如图是抛物线图象的一部分,抛物线的顶点坐标为 , 与x轴的一个交点为 , 点A和点B均在直线上.①;②;③抛物线与x轴的另一个交点为;④方程有两个不相等的实数根;⑤不等式的解集为 . 上述五个结论中,其中正确的结论是(填写序号即可).
12. 如图是抛物线图象的一部分,抛物线的顶点坐标为 , 与x轴的一个交点为 , 点A和点B均在直线上.①;②;③抛物线与x轴的另一个交点为;④方程有两个不相等的实数根;⑤不等式的解集为 . 上述五个结论中,其中正确的结论是(填写序号即可).
三、综合题
-
13. 如图,在一次足球比赛中,守门员在地面 处将球踢出,一运动员在离守门员8米的 处发现球在自己头上的正上方4米处达到最高点 ,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
 (1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)14. 如图,二次函数的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.
(1)、求足球第一次落地之前的运动路线的函数表达式及第一次落地点 和守门员(点 )的距离;(2)、运动员(点 )要抢到第二个落点 ,他应再向前跑多少米?(假设点 、 、 、 在同一条直线上,结果保留根号)14. 如图,二次函数的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.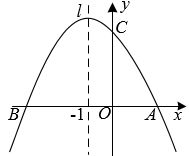 (1)、求点A、B、C的坐标;(2)、若点M在抛物线的对称轴上,且△MAC的周长最小,求点M的坐标;(3)、若点P在x轴上,且△PBC为等腰三角形,请求出所有符合条件的点P的坐标.15. 如图1,抛物线()与轴交于 , 两点,与轴交于点 .
(1)、求点A、B、C的坐标;(2)、若点M在抛物线的对称轴上,且△MAC的周长最小,求点M的坐标;(3)、若点P在x轴上,且△PBC为等腰三角形,请求出所有符合条件的点P的坐标.15. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.四、实践探究题
-
16. 定义:若两个二次函数的图象关于轴对称,则称互为“对称二次函数”.(1)、已知二次函数 , 则它的“对称二次函数”的顶点坐标为.(2)、已知关于的二次函数和 , 其中的图象经过点.若与互为“对称二次函数”,求函数的表达式;(3)、在(2)的条件下,当时,的最小值为-2,请直接写出的值.17. 法国数学家韦达在研究一元二次方程时发现:如果关于x的一元二次方程( , )的两个实数根分别为、 , 那么 , . 习惯上把这个结论称作“韦达定理”.(1)、方程的两个实数根分别为、 , 求和的值.(2)、方程的两个实数根分别为、 , 求的值.(3)、若、为关于x的方程的两个实数根,求的最小值.18. 根据以下素材,探索完成任务。
运用二次函数研究电缆架设问题
素材1
电缆在空中架设时,两端挂起的电缆下垂都可以近似地看成抛物线的形状.如图,在一个斜坡 BD上按水平距离间隔90m架设两个塔柱,每个塔柱固定电缆的位置离地面高度为20m(AB=CD=20m),按如图所示的方式建立平面直角坐标系(x轴在水平方向上).点A,O,E 在同一水平线上,经测量,AO=60m,斜坡BD的坡比为1:10.

素材2
若电缆下垂的安全高度是13.5m,即电缆距离坡面铅直高度的最小值不小于13.5m时,符合安全要求,否则存在安全隐患.
(说明:直线GH⊥x轴且分别与直线BD和抛物线相交于点H,G.点G 距离坡面的铅直高度为GH 的长)
任务1
确定电缆形状
求点 D 的坐标及下垂电缆的抛物线的函数表达式.
任务2
判断电缆安全
上述这种电缆的架设是否符合安全要求? 请说明理由.
任务3
探究安装方法
工程队想在坡比为1:8的斜坡上架设电缆,两个塔柱的高度仍为20m,电缆抛物线的形状与任务1相同.若电缆下垂恰好符合安全高度要求,则两个塔柱的水平距离应为多少米?