【提升版】2024-2025学年浙教版数学九上1.4二次函数的应用同步练习

试卷更新日期：2024-07-24 类型：同步测试

进入出卷网下载

一、选择题

1. 如图1是莲花山景区一座抛物线形拱桥，按图2所示建立平面直角坐标系，得到抛物线解析式为y＝ $- \frac{1}{36} x^{2}$ ，正常水位时水面宽AB为36m，当水位上升5m时水面宽CD为（）

A、10m B、12m C、24m D、48m

查看试题解析
2. 竖直上抛的小球的高度 $h (m)$ 与运动时间 $t (s)$ 的函数表达式为 $h = a t^{2} + b t$ ，若小球在上抛后第 $3 s$ 与第 $7 s$ 时离地面距离相等，则下列时刻中小球的高度最高的是（）

A、第 $4 s$ B、第 $4.8 s$ C、第 $4.9 s$ D、第 $5.2 s$

查看试题解析
3. 将进货单价为50元的某种商品按零售价每个60元出售时，每周能卖出100个，若这种商品零售价每涨价1元，周销售量就减少2个，但物价部门规定，最高售价不能高于成本价的30％，则每周获得的最大利润为（）.

A、80元 B、1000元 C、1750元 D、1800元

查看试题解析
4. 小明在期末体育测试中掷出的实心球的运动路线呈抛物线形，若实心球运动的抛物线的解析式为 $y = - \frac{1}{9} (x - 3)^{2} + k$ ，其中 $y$ 是实心球飞行的高度， $x$ 是实心球飞行的水平距离，已知该同学出手点 $A$ 的坐标为 $(0 ， \frac{16}{9})$ ，则实心球飞行的水平距离 $O B$ 的长度为（）

A、 $7 m$ B、 $7.5 m$ C、 $8 m$ D、 $8.5 m$

查看试题解析
5. 如图，在九年级体育测试中，小朱掷出的实心球的飞行高度y（米）与水平距离x（米）之间的关系大致满足二次函数 $y = - \frac{1}{10} x^{2} + \frac{3}{5} x + \frac{8}{5}$ ，则小朱本次投掷实心球的成绩为（）

A、7m B、7.5m C、8m D、8.5m

查看试题解析
6. 如图是二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象，使 $y \geq - 1$ 成立的 $x$ 的取值范围是（）

A、 $x \geq - 1$ B、 $x \leq - 1$ C、 $- 1 \leq x \leq 3$ D、 $x \leq - 1$ 或 $x ≥ 3$

查看试题解析

7. 已知一次函数

y_{1} = k x + m (k \neq 0)

和二次函数

y_{2} = a x^{2} + b x + c (a \neq 0)

部分自变量和对应的函数值如表：

x	…	-1	0	2	4	5	…
y₁	…	0	1	3	5	6	…
y₂	…	0	-1	0	5	9	…

当y₂＞y₁时，自变量x的取值范围是（）

A、-1＜x＜2 B、4＜x＜5 C、x＜-1或x＞5 D、x＜-1或x＞4

查看试题解析

8. 二次函数y＝ax²＋bx＋c的图象如图所示，下列说法错误的是（）

A、a＜0，b＞0 B、b²﹣4ac＞0 C、方程ax²＋bx＋c＝0的解是x₁＝5，x₂＝﹣1 D、不等式ax²＋bx＋c＞0的解集是0＜x＜5

查看试题解析

二、填空题

9. 如图，九（1）班劳动实践基地位于 $L$ 形围墙的内侧，已知 $∠ A B C = 9 0^{∘}$ ，墙 $A B$ 长7米，墙 $B C$ 长3米．同学们准备用10米长的围栏，在基地内围出一块矩形菜地（可利用围墙）．请问他们能围出的最大面积是米² ．

查看试题解析
10. 在为期3天的广安市第五届运动会（青少年组）三人制篮球比赛中，某同学进行了一次投篮，篮球准确落入篮框内，建立如图所示的平面直角坐标系，篮球的运行轨迹可看作抛物线 $y = - x^{2} + 2 x + 2.6$ 的一部分，则篮球在空中运行的最大高度为 $m$ ．

查看试题解析
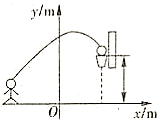11. 小明和小强做弹球游戏，如图1，小明向斜坡找一个乒乓球，乒乓球弹起的运行路线是一条抛物线，乒乓球落地后又弹起，第二次弹起的运行路线和第一次运行路线的抛物线形状相同．小强在地面立一块高度为 $0.4 m$ 的木板，以斜坡底端 $O$ 为坐标原点，地面水平线为 $x$ 轴，取单位长度为 $1 m$ ，建立如图2所示的平面直角坐标系，乒乓球的大小忽略不计，经测量发现，拋球点 $A$ 的坐标为 $(- 1 ， 3.36)$ ，第一次弹起的运行路线最高点坐标为 $(- 0.5 ， 3.61)$ ，第二次弹起的最大高度为 $1.21 m$ ．

(1)、求乒乓球第一次落地点B距斜坡低端O的距离是 $m$ ；

(2)、为了确保乒乓球在第二次下落时能落在木板上，小强将木板立在到斜坡底端O的最小距离是 $m$ ．

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 为常数， $c < 0)$ 经过 $(1 ， 1)$ ， $(m ， 0)$ ， $(n ， 0)$ 三点，且 $n ≥ 3$ .
下列四个结论：① $b < 0$ ；② $\frac{4 a c - b^{2}}{4 a} > 1$ ；③当 $n = 3$ 时，若点 $(2 ， t)$ 在该抛物线上，则 $t > 1$ ；④若关于x的一元二次方程 $a x^{2} + b x + c = x$ 有两个相等的实数根，则 $0 < m ≤ \frac{1}{3}$ .
其中正确的是（填序号即可）.

查看试题解析

三、解答题

13. 李大爷每天到批发市场购进某种水果进行销售，这种水果每箱10千克，批发商规定：整箱购买，一箱起售，每人一天购买不超过10箱；当购买1箱时，批发价为8.2元/千克，每多购买1箱，批发价每千克降低0.2元.根据李大爷的销售经验，这种水果售价为12元/千克时，每天可销售1箱；售价每千克降低0.5元，每天可多销售1箱.

(1)、请求出这种水果批发价 $y$ （元/千克）与购进数量 $x$ （箱）之间的函数关系式；

(2)、若每天购进的这种水果需当天全部售完，请你计算，李大爷每天应购进这种水果多少箱，才能使每天所获利润最大？最大利润是多少？

查看试题解析
14. 如图1所示是一座古桥，桥拱截面为抛物线，如图2，AO，BC是桥墩，桥的跨径AB为20m，此时水位在OC处，桥拱最高点P离水面6m，在水面以上的桥墩AO，BC都为2m．以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系，其中x（m）是桥拱截面上一点距桥墩AO的水平距离，y（m）是桥拱截面上一点距水面OC的距离．

(1)、求此桥拱截面所在抛物线的表达式；

(2)、有一艘游船，其左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在河中航行．当水位上涨2m时，水面到棚顶的高度为3m，遮阳棚宽12m，问此船能否通过桥洞？请说明理由．

查看试题解析

四、实践探究题

15. 根据以下材料，探索完成任务：

智能浇灌系统使用方案
材料			如图1是一款智能浇灌系统，水管OP垂直于地面并可以随意调节高度（OP最大高度不超过2.4m），浇灌花木时，喷头P处会向四周喷射水流形成固定形状的抛物线，水流落地点M与点O的距离即为最大浇灌距离，各方向水流落地点形成一个以点O为圆心，OM为半径的圆形浇灌区域．当喷头P位于地面与点O重合时，某一方向的水流上边缘形成了如图2的抛物线，经测量， $O M = 2 m$ ，水流最高时距离地面0.1m．如图3，农科院将该智能浇灌系统应用于一个长8m，宽6m的矩形试验田中，水管放置在矩形中心O处．
问题解决
任务1	确定水流形状	在图2中建立合适的平面直角坐标系，求抛物线的函数表达式．
任务2	探究浇灌最大区域	当调节水管OP的高度时，浇灌的圆形区域面积会发生变化，请你求出最大浇灌圆形区域面积．（结果保留 $π$ ）
任务3	解决具体问题	若要保证浇灌区域能完全覆盖矩形试验田，则水管OP至少需要调节到什么高度？

查看试题解析

16. 【综合与实践】数学来源于生活，同时数学也可以服务于生活.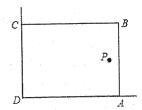
【知识背景】如图，校园中有两面直角围墙，墙角内的P处有一古棵树与墙 $C D$ ， $A D$ 的距离分别是 $15 m$ 和 $6 m$ ，在美化校园的活动中，某数学兴趣小组想借助围墙（两边足够长），用 $28 m$ 长的篱笆围成一个矩形花园 $A B C D$ （篱笆只围 $A B$ ， $B C$ 两边），设 $A B = x m$ .
【方案设计】设计一个矩形花园，使之面积最大，且要将古棵树P围在花园内（含边界，不考虑树的粗细）.
【解决问题】思路：把矩形 $A B C D$ 的面积S与边长x（即 $A B$ 的长）的函数解析式求出，并利用函数的性质来求面积的最大值即可.

(1)、请用含有x的代数式表示 $B C$ 的长；

(2)、花园的面积能否为 $192 m^{2}$ ?若能，求出x的值，若不能，请说明理由；

(3)、求面积S与x的函数解析式，写出x的取值范围；并求当x为何值时，花园面积S最大?

查看试题解析

五、综合题

17. 公路上正在行驶的甲车发现前方 $20 m$ 处沿同一方向行驶的乙车后，开始减速，减速后甲车行驶的路程 $s ($ 单位： $m)$ 、速度 $v ($ 单位： $m / s)$ 与时间 $t ($ 单位： $s)$ 的关系分别可以用二次函数和一次函数表示，其图象如图所示．

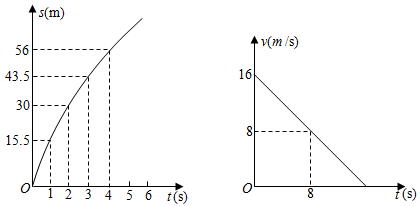(1)、直接写出 $s$ 关于 $t$ 的函数关系式和 $v$ 关于 $t$ 的函数关系式 $($ 不要求写出 $t$ 的取值范围 $)$

(2)、当甲车减速至 $9 m / s$ 时，它行驶的路程是多少？

(3)、若乙车以 $10 m / s$ 的速度匀速行驶，两车何时相距最近，最近距离是多少？

查看试题解析

【提升版】2024-2025学年浙教版数学九上1.4二次函数的应用 同步练习

一、选择题

二、填空题

三、解答题

四、实践探究题

五、综合题

【提升版】2024-2025学年浙教版数学九上1.4二次函数的应用同步练习