【提升版】2024-2025学年浙教版数学九上1.2二次函数的图象 同步练习
试卷更新日期:2024-07-24 类型:同步测试
一、选择题
-
1. 抛物线的顶点坐标为( )A、 B、 C、 D、2. 将抛物线 向上平移2个单位,则得到的抛物线表达式为( )
A、 B、 C、 D、3. 已知二次函数的图象如图所示,则点所在的象限是( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知直线经过第一、三、四象限,则抛物线可能是下列中的( )A、
A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知直线经过第一、三、四象限,则抛物线可能是下列中的( )A、 B、
B、 C、
C、 D、
D、 5. 若点在二次函数图象的对称轴上,则点的坐标可能是( )A、 B、 C、 D、6. 已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
5. 若点在二次函数图象的对称轴上,则点的坐标可能是( )A、 B、 C、 D、6. 已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
A、 B、 C、 D、7. 在同一坐标系内,函数y=kx2和y=kx-2(k≠0)的图象大致如图( )A、 B、
B、 C、
C、 D、
D、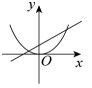 8. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )
8. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )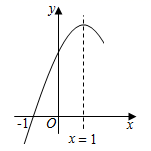 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
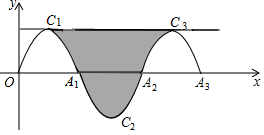
9. 二次函数的顶点坐标为10. 已知一个二次函数图象的形状与抛物线相同,它的顶点坐标为 , 则该二次函数的表达式为.11. 将抛物线先向下平移1个单位长度后,再向左平移5个单位长度,所得抛物线相应的函数表达式是.12. 如图,一段抛物线: ,记为 ,它与x轴交于两点O, ;将 绕 旋转 得到 ,交x轴于 ;将 绕 旋转 得到 ,交x轴于 ,过抛物线 , 顶点的直线与 、 、 围成的如图中的阴影部分,那么该阴影部分的面积为.
三、解答题
-
13. 已知二次函数的图象经过点 .(1)、求该二次函数的表达式.(2)、求这个二次函数图象的顶点坐标.14. 如图,抛物线与轴交于点、 , 是抛物线的顶点,▱的顶点在轴上.
 (1)、求的值;(2)、若抛物线沿其对称轴向上平移后恰好经过点 , 求平移后抛物线的解析式.
(1)、求的值;(2)、若抛物线沿其对称轴向上平移后恰好经过点 , 求平移后抛物线的解析式.四、综合题
