【基础版】2024-2025学年浙教版数学九上1.1二次函数 同步练习

试卷更新日期：2024-07-24 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 下列函数中，是二次函数的是（    ）
    A、y＝3x﹣2 B、y＝ 1x2 C、y＝x2＋1 D、y＝（x﹣1）2﹣x2

    查看试题解析

  • 2. 已知y=(m+1)xm2+1+2x−3是二次函数，则m的值为（    ）
    A、0 B、1 C、－1 D、1或－1

    查看试题解析

  • 3. 一元二次方程5x2−2x+2=0的一次项系数是（    ）
    A、5 B、−2 C、2 D、0

    查看试题解析

  • 4. 已知一个直角三角形两直角边长的和为10，设其中一条直角边长为x，则直角三角形的面积y与x之间的函数关系式是（ ）
    A、y=-12x2+5x B、y=-x2+10x C、y=12x2+5x D、y=x2+10x

    查看试题解析

  • 5. 已知某种产品的成本价为30元/千克，经市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=-2x+80．设这种产品每天的销售利润为w（元），则w与x之间的函数表达式为（ ）
    A、w=(x－30)(－2x+80) B、w=x(－2x+80) C、w=30(－2x+80) D、w=x(－2x+50)

    查看试题解析

  • 6. 已知y关于x的二次函数解析式为y=(2−m)x|m| ， 则m=（ ）
    A、±2 B、1 C、−2 D、±1

    查看试题解析

  • 7. 如图，正方形ABCD和⊙O的周长之和为20cm ， 设圆的半径为xcm ， 正方形的边长为ycm ， 阴影部分的面积为Scm2 ． 当x在一定范围内变化时，y和S都随x的变化而变化，则y与x，S与x满足的函数关系分别是（   ）

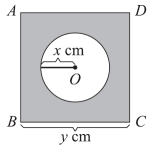    A、一次函数关系，一次函数关系 B、一次函数关系，二次函数关系 C、二次函数关系，二次函数关系 D、二次函数关系，一次函数关系

    查看试题解析

  • 8. 二次函数y=x2−6x−1的二次项系数、一次项系数和常数项分别是（    ）
    A、1，-6，-1 B、1，6，1 C、0，-6，1 D、0，6，-1

    查看试题解析

二、填空题

  • 9. 小聪在画一个二次函数的图象时，列出了下面几组y与x的对应值：

    x

    …

    0

    1

    2

    3

    4

    5

    …

    y

    …

    5

    0

    -3

    -4

    -3

    0

    …

    该二次函数的解析式是 ．

    查看试题解析

  • 10. 若关于x的函数y=xa2+1−7x的图象是抛物线，则a的值是 ．

    查看试题解析

  • 11. 若y=(m−3)xm2−5m+8+2x−3是关于x的二次函数，则m的值是 ．

    查看试题解析

  • 12. 如图，用长为20cm的篱笆，一边利用墙(墙足够长)围成一个长方形花园，设花园的宽AB为xcm ， 围成的花圃面积为ycm2 ， 则y关于x的函数表达式为 ．

    查看试题解析

三、解答题

  • 13. 写出下表中二次函数的二次项系数、一次项系数和常数项。

    函数表达式

    二次项系数

    一次项系数

    常数项

    y=x2-2x-1

    		   

    y=3x2+5

    		   

    y=3x-12x2

    		   

    y=2(x-1)(x+2)

    		   

    y=(x-2)2-1

    		   

    查看试题解析

  • 14. 抛物线y＝ax2＋bx＋c过(－3，0)，(1，0)两点，与y轴的交点为(0，4)，求抛物线的解析式．

    查看试题解析

  • 15. 写出下列函数的表达式，并指出哪些是二次函数，哪些是一次函数，哪些是反比例函数．
    (1)、正方形的面积S关于它的边长x的函数．
    (2)、圆的周长C关于它的半径r的函数．
    (3)、圆的面积S关于它的半径r的函数．
    (4)、当菱形的面积S一定时，它的一条对角线的长度y关于另一条对角线的长度x的函数．

    查看试题解析

四、综合题

  • 16. 如图，进行绿地的长、宽各增加xm．

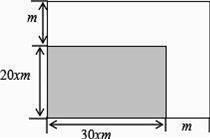    (1)、写出扩充后的绿地的面积y（ m2 ）与x（m）之间的函数关系式；
    (2)、若扩充后的绿地面积y是原矩形面积的2倍，求x的值．

    查看试题解析

  • 17. 如图，在△ABC中，∠B＝90°，AB＝12mm，BC＝24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，设运动的时间为ts，四边形APQC的面积为ymm2 ．

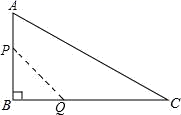    (1)、y与t之间的函数关系式；
    (2)、求自变量t的取值范围；
    (3)、四边形APQC的面积能否等于172mm2 ． 若能，求出运动的时间；若不能，说明理由．

    查看试题解析