贵州省黔东南州从江县东朗中学2023-2024学年七年级下学期数学6月质量监测试卷
试卷更新日期:2024-07-22 类型:月考试卷
一、选择题(每小题3分,共36分.以下每小题均有A、B、C、D四个选项,其中只有一个选项正确)
-
1. 比-2小的数是( )A、-2 B、2 C、- D、-π2. 下列各数是无理数的是( )A、0 B、-1 C、 D、3.143. 如图所示,已知直线c与直线a,b都相交.若a∥b,∠1=85°,则∠2等于( )
 A、110° B、105° C、100° D、95°4. 若点A(a,3)在y轴上,则点B(a-2,a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列等式成立的是( )A、=±4 B、=±4 C、2-= D、=26. 下列整数中,与最接近的整数是( )A、3 B、4 C、5 D、67. 为了解我校七年级800名学生期中数学考试情况,从中抽取了200名学生的数学成绩进行统计.下列判断:①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④200名学生是总体的一个样本;⑤200名学生是样本容量.其中正确的判断有( )A、1个 B、2个 C、3个 D、4个8. 已知点P(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、
A、110° B、105° C、100° D、95°4. 若点A(a,3)在y轴上,则点B(a-2,a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列等式成立的是( )A、=±4 B、=±4 C、2-= D、=26. 下列整数中,与最接近的整数是( )A、3 B、4 C、5 D、67. 为了解我校七年级800名学生期中数学考试情况,从中抽取了200名学生的数学成绩进行统计.下列判断:①这种调查方式是抽样调查;②800名学生是总体;③每名学生的数学成绩是个体;④200名学生是总体的一个样本;⑤200名学生是样本容量.其中正确的判断有( )A、1个 B、2个 C、3个 D、4个8. 已知点P(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、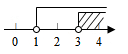 B、
B、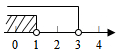 C、
C、 D、
D、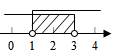 9. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组为( )A、 B、 C、 D、10. 点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是( )A、(3,3) B、(3,-3) C、(6,-6) D、(3,3)或(6,-6)11. 一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度是( )A、先向左转130°,再向左转50° B、先向左转60°,再向右转60° C、先向左转50°,再向右转40° D、先向左转50°,再向左转40°12. 若关于x的一元一次不等式组恰好有2个整数解,且关于y的方程y-3=3k-y的解为非正数,则符合条件的所有整数k的和为( )A、-5 B、-3 C、-6 D、6
9. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组为( )A、 B、 C、 D、10. 点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是( )A、(3,3) B、(3,-3) C、(6,-6) D、(3,3)或(6,-6)11. 一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度是( )A、先向左转130°,再向左转50° B、先向左转60°,再向右转60° C、先向左转50°,再向右转40° D、先向左转50°,再向左转40°12. 若关于x的一元一次不等式组恰好有2个整数解,且关于y的方程y-3=3k-y的解为非正数,则符合条件的所有整数k的和为( )A、-5 B、-3 C、-6 D、6二、填空题(每小题4分,共16分)
-
13. 如图所示,已知直线a,b交于点O,∠1=30°,那么∠2的度数为.
 14. 若a,b互为相反数,c为8的立方根,则2a+2b-c=.15. 定义新运算:a⊕b=1-ab,则不等式x⊕2≥-3的非负整数解的个数为.16. 如图所示,面积为4的正方形ABCD的边AB在数轴上,且点B表示的数为1.将正方形ABCD沿着数轴水平移动,移动后的正方形记为A'B'C'D' , 点A,B,C,D的对应点分别为A' , B' , C' , D' , 移动后的正方形A'B'C'D'与原正方形ABCD重叠部分图形的面积记为S.当S=1时,数轴上点B'表示的数是.
14. 若a,b互为相反数,c为8的立方根,则2a+2b-c=.15. 定义新运算:a⊕b=1-ab,则不等式x⊕2≥-3的非负整数解的个数为.16. 如图所示,面积为4的正方形ABCD的边AB在数轴上,且点B表示的数为1.将正方形ABCD沿着数轴水平移动,移动后的正方形记为A'B'C'D' , 点A,B,C,D的对应点分别为A' , B' , C' , D' , 移动后的正方形A'B'C'D'与原正方形ABCD重叠部分图形的面积记为S.当S=1时,数轴上点B'表示的数是.
三、解答题(本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤)
-
17.(1)、计算:+|3-π|-;(2)、求3(x-1)3=81中的x的值.18. 下面是小义同学解二元一次方程组的过程:
解方程组:
解:①-②得7y-5y=-24…第一步,
2y=-24…第二步,
y=-12…第三步,
把y=-12代入①,得x=39…第四步,
所以原方程组的解为…第五步.
(1)、以上解题步骤,小义从第步开始出现错误;(2)、请你写出正确的解答过程.19. 解不等式组:并把解集在数轴上表示出来. 20. 2023年12月4日是我国第23个“法制宣传日”,我校举行了主题“学法,知法,懂法,守法”的普法知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
20. 2023年12月4日是我国第23个“法制宣传日”,我校举行了主题“学法,知法,懂法,守法”的普法知识竞赛.为了了解本次知识竞赛成绩的分布情况,从参赛学生中随机抽取了150名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分
频数
频率
60≤x<70
15
0.1
70≤x<80
a
0.2
80≤x<90
45
b
90≤x<100
60
0.4
(1)、表中a=_ , b=_;(2)、请补全频数分布直方图;(3)、若80分及其以上为优秀,该校现有1200名学生,请你估计我校成绩优秀的学生有多少名?(4)、结合以上信息,请你给该校关于普法方面提出一条合理化的建议.21. 如图所示,直线AB,CD相交于点O,OF⊥AB,垂足为O,且OF平分∠COE,若∠BOC∶∠BOD=5∶1. (1)、求∠AOC的度数;(2)、求∠EOF的度数.22. 如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明理由.
(1)、求∠AOC的度数;(2)、求∠EOF的度数.22. 如图所示,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明理由. 23. 如图所示,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(4,2),B(1,0),C(5,-3),三角形ABC中任意一点P(x0 , y0),经平移后对应点为P'(x0-6,y0+2),将三角形ABC作同样的平移得到三角形A'B'C' , 点A,B,C的对应点分别为A' , B' , C'.
23. 如图所示,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(4,2),B(1,0),C(5,-3),三角形ABC中任意一点P(x0 , y0),经平移后对应点为P'(x0-6,y0+2),将三角形ABC作同样的平移得到三角形A'B'C' , 点A,B,C的对应点分别为A' , B' , C'. (1)、点A'的坐标为 , 点B'的坐标为;(2)、①画出三角形A'B'C';
(1)、点A'的坐标为 , 点B'的坐标为;(2)、①画出三角形A'B'C';②求出三角形A'B'C'的面积.
24. 大数据显示,新能源汽车需求量正倍速的增长.为满足客户需求,现某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解1辆A型汽车、2辆B型汽车的进价共计75万元;2辆A型汽车、3辆B型汽车的进价共计130万元.(1)、A,B两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划以不超过300万元购进以上两种型号的新能源汽车共10辆,并且该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,假如这些新能源汽车全部售出,至少要获得62000元的利润,该公司有哪几种购进方案?哪种方案获得的利润最多,最多利润是多少?25.(1)、阅读理解数学兴趣小组的同学在学习了平行线的性质“两直线平行,同旁内角互补”后,做了如下思考.

如图(1)所示,∵AB∥CD,
∴∠AEF+∠CFE=180°.
如图(2)所示,点E,F分别在直线AB,CD上,点P为直线AB,CD内一点(点E,F,P不在同一条直线上),连接PE,PF.得出结论:∠EPF=∠AEP+∠CFP.
证明过程如下:
如图(3)所示,过点P作PH∥AB,
∵AB∥CD,
∴PH∥CD.
∴∠CFP=∠FPH( ),
∵PH∥AB,
∴∠AEP=∠EPH.
∵∠EPF=∠EPH+∠FPH,
∴∠EPF=∠AEP+∠CFP( ).
请补充完成上面的证明过程.
(2)、请直接用(1)的结论解决下列问题.问题解决

如图(4)所示,分别作∠BEP和∠DFP的平分线交于点M,若∠EPF=140°.求∠EMF的度数.
(3)、拓展探究如图(5)所示,分别作∠BEP和∠DFP的平分线交于点M,再分别作∠AEM和∠CFM的平分线交于点N,若∠EPF=α,∠EMF=β,∠ENF=θ,探究α,β,θ的关系式,并写出该关系式及解答过程.