江西省南昌市一中教育集团2023-2024学年七年级下学期期中数学试题

试卷更新日期：2024-07-19 类型：期中考试

进入出卷网下载

一、选择题（本大题共6小题，每小题3分，共18分）

1. 16的平方根是（）．

A、4 B、 $\pm 4$ C、 $- 4$ D、 $\pm 8$

查看试题解析
2. 下列实数中，属于无理数的是（）

A、 $\frac{1}{3}$ B、 $\sqrt{7}$ C、3.14159 D、 $\sqrt{36}$

查看试题解析
3. 点 $A (1, - \sqrt{2})$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，AD是∠EAC的平分线，AD $/ /$ BC ， ∠B＝30°，则∠C为（）．

A、15° B、20° C、25° D、30°

查看试题解析
5. 在平面直角坐标系中，将点 $P (- 2, 1)$ 向右平移3个单位长度，再向上平移4个单位长度得到点P的坐标是 $($ ）

A、 $(1, 5)$ B、 $(1, - 3)$ C、 $(- 5, 5)$ D、 $(- 5, - 3)$

查看试题解析
6. 将一副直角三角板按如图所示的方式叠放在一起，若AC∥DE，则∠BAE的度数为（）

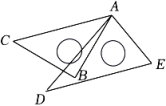A、50° B、65° C、75° D、85°

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

7. 写出一个比 $\sqrt{3}$ 大且比 $\sqrt{10}$ 小的整数是.

查看试题解析
8. 已知点A(m﹣1，m+4)在y轴上，则点A的坐标是.

查看试题解析
9. 如图， $△ A B C$ 是等腰直角三角形，直线 $a ∥ b$ ，若 $∠ 1 = 125 °$ ，则 $∠ 2$ 的度数是．

查看试题解析
10. 规定运算：（a*b）=｜a－b｜，其中a、b为实数，则（ $\sqrt{7}$ *3）+ $\sqrt{7}$ =.

查看试题解析
11. 如下图所示，在平面直角坐标系中，点P的坐标为 $(1 ， 2)$ ，点Q是x轴上的一个动点，当线段 $P Q$ 的长最小时，点Q的坐标为．

查看试题解析
12. 在“折纸与平行”的拓展课上，小陈老师布置了一个任务：如图，有一张三角形纸片 $A B C$ ， $∠ B = 30 °$ ， $∠ C = 50 °$ ，点D是 $A B$ 边上的固定点 $(B D < \frac{1}{2} A B)$ ，请在 $B C$ 上找一点E ，将纸片沿 $D E$ 折叠（ $D E$ 为折痕），点B落在点F处，使 $E F$ 与 $△ A B C$ 的一边平行，则 $∠ B E D$ 为度．

查看试题解析

三、解答题（本大题共5小题，每小题6分，共30分）

13.

(1)、解方程 $4 x^{2} - 16 = 0$ ；

(2)、计算： $\sqrt{16} + | 1 - \sqrt{2} | + \sqrt[3]{- 27}$ ．

查看试题解析
14. 已知 $3 a + 1$ 的算术平方根是5， $4 - 2 b$ 的立方根是2，求 $a - b$ 的值．

查看试题解析
15. 如图，AB∥CD ， CE平分∠ACD ， ∠A=108°，求∠AEC 的度数．

查看试题解析
16. 如图，所有小正方形的边长都为 $1$ ， A、 $B$ 、 $C$ 都在格点上（小正方形的顶点叫做格点）．请仅用无刻度直尺完成画图（不要求写画法）．

(1)、作线段 $C D$ ， $C D ∥ A B$ ， $C D = A B$ ；

(2)、作线段 $A H$ ， $A H ⊥ A B$ 于点A ，交 $B C$ 于点 $H$ ．

查看试题解析
17. 如图，在平面直角坐标系中，有三点A(1，0)，B(3，0)，C(4，－2)．

(1)、画出三角形ABC；

(2)、将三角形ABC先向左平移4个单位长度，再向上平移3个单位长度，画出平移后的三角形DEF，并写出D、E、F三点的坐标；

(3)、求三角形ABC的面积．

查看试题解析

四、解答题（本大题共3小题，每小题8分，共24分）

18. 定义：在平面直角坐标系中，对于任意两点A(a ， b)， B(c ， d)，若点T(x ， y)满足 $x = \frac{a + c}{3}$ ， $y = \frac{b + d}{3}$ ，那么称点T是点A和B的衍生点．例如：M (-2，5)，N(8，-2)，则点T (2，1)是点M和N的衍生点．
已知点D (3，0)，点E (m ， m+2)，点T(x ， y)是点D和E的衍生点．

(1)、若点E (4，6)，则点T的坐标为；

(2)、请直接写出点T的坐标(用m表示)；

(3)、若直线ET交x轴于点H ，当∠DHT=90°时，求点E的坐标．

查看试题解析
19. 已知点 $P (2 a - 2, a + 5)$ ，解答下列各题：

(1)、若点P在x轴上．求出点P的坐标；

(2)、若点Q的坐标为 $(4, 5)$ ，直线 $P Q ∥ x$ 轴，求出点P的坐标；

(3)、若点P到x轴、y轴的距离相等，求出点P的坐标，并说出P点所在的象限．

查看试题解析
20. 如图，已知 $F$ ， $E$ 分别是射线 $A B$ ， $C D$ 上的点．连接 $A C$ ， $A E$ 平分 $∠ B A C$ ， $E F$ 平分 $∠ A E D$ ， $∠ 2 = ∠ 3$ ．

(1)、试说明 $A B ∥ C D$ ；

(2)、若 $∠ A F E - ∠ 2 = 30 °$ ，求 $∠ A F E$ 的度数．

查看试题解析

五、解答题（本大题共2小题，每小题9分，共18分）

21. 已知直线 $l_{1} ∥ l_{2}$ ， $l_{3}$ 、 $l_{4}$ 和 $l_{1}$ 、 $l_{2}$ 分别交于点A、B、C、D ，点P直线 $l_{3}$ 或 $l_{4}$ 上，且不与点A、B、C、D重合．记 $∠ A E P = ∠ 1$ ， $∠ P F B = ∠ 2$ ， $∠ E P F = ∠ 3$

(1)、若点P在图（1）位置时，若 $∠ 1 = 30 °$ ， $∠ 3 = 70 °$ ，求 $∠ 2$ 的度数；

(2)、若点P在图（2）位置时，请直接写出 $∠ 1$ 、 $∠ 2$ 、 $∠ 3$ 之间的关系；

(3)、若点P在图（3）位置时，写出 $∠ 1$ 、 $∠ 2$ 、 $∠ 3$ 之间的关系并给予证明．

查看试题解析
22. 阅读下面的材料：如图 $①$ ，若线段 $A B$ 在数轴上， $A$ ， $B$ 点表示的数分别为 $a$ ， $b$ $(b > a)$ ，则线段 $A B$ 的长（点 $A$ 到点 $B$ 的距离）可表示为 $A B = b - a$ ，
请用上面材料中的知识解答下面的问题：
如图 $②$ ，一个点从数轴上的原点开始，先向左移动 $1 c m$ 到达 $A$ 点，再向左移动 $2 c m$ 到达 $B$ 点，然后向右移动 $7 c m$ 到达 $C$ 点，用 $1$ 个单位长度表示 $1 c m$ ．

(1)、请你在数轴上表示出 $A$ ， $B$ ， $C$ 三点的位置，并直接写出线段 $A C$ 的长度；

(2)、若数轴上有一点 $D$ ，且 $A D = 4 c m$ ，则点 $D$ 表示的数是什么？

(3)、若将点 $A$ 向右移动 $x c m$ ，请用代数式表示移动后的点表示的数？

(4)、若点 $B$ 以每秒 $2 c m$ 的速度向左移动至点 $P_{1}$ ，同时点 $A$ 、点 $C$ 分别以每秒 $1 c m$ 和 $4 c m$ 的速度向右移动至点 $P_{2}$ 、点 $P_{3}$ ，设移动时间为 $t$ 秒，试探索： $P_{3} P_{2} - P_{1} P_{2}$ 的值是否会随着 $t$ 的变化而变化？请说明理由．

查看试题解析

六、解答题（本大题12分）

23. 如图，直线 $A B ∥ C D$ ，直线 $F F$ 与 $A B$ ， $C D$ 分别交于点 $G$ ， $H$ ， $∠ E H D = α (0 ° < α < 90 °)$ ．小安将一个含 $30 °$ 角的直角三角板 $P M N$ 按如图①放置，使点 $N$ ， $M$ 分别在自线 $A B$ ， $C D$ 上，且在点 $C$ 、 $H$ 的右测， $∠ P = 90 °$ ， $∠ P M N = 60 °$ ．

(1)、填空： $∠ P N B + ∠ P M D =$ ；

(2)、若 $∠ M N G$ 的平分线 $N O$ 交直线 $C D$ 于点 $O$ ，如图②
①当 $N O ∥ E F ， P M ∥ E F$ 时，求 $α$ 的度数；
②小安将三角板 $P M N$ 沿直线 $A B$ 左右移动，保持 $P M ∥ E F$ ，点N、M分别在直线 $A B$ 和直线 $C D$ 上移动．请直接写出 $∠ M O N$ 的度数（用含 $α$ 式子表示）．

查看试题解析