【培优版】北师大版数学九上2.3用公式法解一元二次方程同步练习

试卷更新日期：2024-07-17 类型：同步测试

进入出卷网下载

一、选择题

1. 若a、b是关于x的一元二次方程x²－6x＋n＋1＝0的两根，且等腰三角形三边长分别为a、b、4，则n的值为（）

A、8 B、7 C、8或7 D、9或8

查看试题解析
2. 如图是一张矩形纸片 $A B C D$ ，点 $E$ ， $G$ 分别在边 $B C$ ， $A B$ 上，把 $△ D C E$ 沿直线 $D E$ 折叠，使点 $C$ 落在对角线 $B D$ 上的点 $F$ 处 $；$ 把 $△ D A G$ 沿直线 $D G$ 折叠，使点 $A$ 落在线段 $D F$ 上的点 $H$ 处， $H F = 1$ ， $B F = 8$ ，则矩形 $A B C D$ 的面积为（）

A、 $420$ B、 $360$ C、 $420 \sqrt{2}$ D、 $360 \sqrt{2}$

查看试题解析
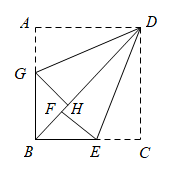3. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0),$ 下列说法：①当 $b = a + c$ 时，则方程 $a x^{2} + b x + c = 0$ 一定有一根为 $x = - 1$ ；②若 $a b > 0 ， b c < 0 ，$ 则方程 $a x^{2} + b x + c = 0$ 一定有两个不相等的实数根；③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ ；④若 $b = 2 a + 3 c$ ，则方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．其中正确的是（）

A、①② B、①③ C、①②④ D、②③④

查看试题解析
4. 已知关于x的一元二次方程 $a x^{2} + b x + c = 0$ 与 $c x^{2} + b x + a = 0$ ，下列判断错误的是（）

A、若方程 $a x^{2} + b x + c = 0$ 有两个实数根，则方程 $c x^{2} + b x + a = 0$ 也有两个实数根； B、如果m是方程 $a x^{2} + b x + c = 0$ 的一个根，那么 $\frac{1}{m}$ 是 $c x^{2} + b x + a = 0$ 的一个根； C、如果方程 $a x^{2} + b x + c = 0$ 与 $c x^{2} + b x + a = 0$ 有一个根相等，那么这个根是1； D、如果方程 $a x^{2} + b x + c = 0$ 与 $c x^{2} + b x + a = 0$ 有一个根相等，那么这个根是1或-1.

查看试题解析
5. 若关于x的方程 $(a + 2) x^{2} - 3 x + 1 = 0$ 有实数根，则a的取值范围是（）

A、 $a \leq \frac{1}{4}$ 且 $a \neq - 2$ B、 $a \leq \frac{1}{4}$ C、 $a < \frac{1}{4}$ 且 $a \neq - 2$ D、 $a < \frac{1}{4}$

查看试题解析
6. 若等腰三角形（不等边）的一边长为3，另两边长是关于x的方程x²﹣8x+2m+2＝0的两个根，则m的值为（　　）

A、7 B、﹣7或6 C、6.5或7 D、6.5

查看试题解析
7. 利用公式解可得一元二次方程式2x²﹣9x+8＝0的两解为a、b ，且a＞b ，则a的值为（　　）

A、 $\frac{9 + \sqrt{17}}{4}$ B、 $\frac{9 - \sqrt{17}}{4}$ C、 $\frac{- 9 + \sqrt{17}}{4}$ D、 $\frac{- 9 - \sqrt{17}}{4}$

查看试题解析
8. 老师设计了接力游戏，用合作的方式完成判断一元二次方程根的情况，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成判断.过程如图所示：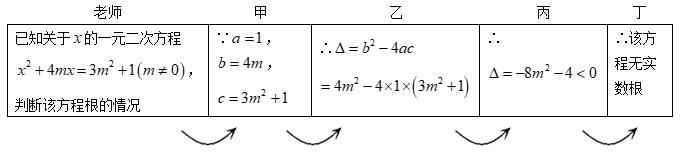
接力中，自己负责的一步出现错误的是（）

A、只有甲 B、甲和乙 C、乙和丙 D、乙和丁

查看试题解析

二、填空题

9. 关于x的一元二次方程 $a x^{2} - 8 x + b = 0$ 有两个相等的实数根，a与b的乘积是．

查看试题解析
10. 若关于x的一元二次方程x²﹣3x+c＝0有两个不相等的实数根，则c的值可以是 .（写出一个即可）

查看试题解析
11. 若 $a^{2} + 5 a b - b^{2} = 0$ ，则 $\frac{a}{b}$ 的值为．

查看试题解析
12. 方程x²-2|x+4|-27=0的所有根的和为．

查看试题解析
13. 有6张正面分别标有数 $- 2 ， - 1 ， 0 ， 1 ， 2 ， 3$ 的不透明卡片，它们除数不同外其余全部相同.现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数记为 $a$ ，将该数加1记为 $b$ ，则数a，b使得关于 $x$ 的一元二次方程 $a x^{2} + b x + \frac{a}{4}$ $= 0$ 有解的概率是.

查看试题解析

三、解答题

14. 已知关于x的一元二次方程x²﹣（4m+1）x+3m²+m=0．

(1)、求证：无论m取何实数时，原方程总有两个实数根；

(2)、若原方程的两个实数根一个大于2，另一个小于7，求m的取值范围；

(3)、抛物线y=x²﹣（4m+1）x+3m²+m与x轴交于点A．B，与y轴交于点C，当m取（2）中符合题意的最小整数时，将此抛物线向上平移n个单位，使平移后得到的抛物线顶点落在△ABC的内部（不包括△ABC的边界），求n的取值范围（直接写出答案即可）．

查看试题解析
15. 定义：如果一个数的平方等于﹣1，记为i²＝﹣1，这个数i叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为a+bi（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．
例如计算：（2+i）+（3﹣4i）＝（2+3）+（i﹣4i）＝5﹣3i

(1)、填空：i³＝， i⁴＝．

(2)、填空：①（2+i）（2﹣i）＝； ②（2+i）²＝．

(3)、若两个复数相等，则它们的实部和虚部必须分别相等，完成下列问题：已知，（x+y）+3i＝1﹣（x﹣y）i，（x，y为实数），求x，y的值．

(4)、试一试：请利用以前学习的有关知识将 $\frac{1 + i}{1 - i}$ 化简成a+bi的形式．

(5)、解方程：x²﹣2x+4＝0．

查看试题解析
16. [探究与应用]
公式法是解一元二次方程常用的方法之一，应用比较广泛，能适用于解所有的一元二次方程．
[观察与分析]小张在解方程x²-6x= 7时，他的解答过程如下：
解：∵a=1， b=-6，c=7，(第一步)
∴△=b²-4ac=(-6)²-4×1×7=8> 0．(第二步)
∴方程有两个不相等的实数根
x= $\frac{6 \pm \sqrt{8}}{2}$ = $\frac{6 \pm 2 \sqrt{2}}{2}$ = $3 \pm \sqrt{2}$ (第三步)
∴x₁=3+ $\sqrt{2}$ ， x₂=3- $\sqrt{2}$ ． (第四步)
[思考与应用]

(1)、小张的解答过程是否正确？

(2)、如果你认为正确，请你用另一种方法来解这个方程，看看得到的结果是否一致；
如果你认为不正确，请指出小张从第几步开始出错，并用小张的方法重新解方程．

查看试题解析
17. 已知：方程 x²-（2k+3）x+k²+3k+2=0是关于x的一元二次方程，

(1)、判断此方程根的情况，并说明理由；

(2)、若a，b，c△ABC的三边，c= 5，且a，b是一元二次方程x²-（2k+3）x+k²+3k+2=0的两根．
①k何值时，△ABC是等腰三角形，并求它的周长．

②k为何值时，△ABC是以c为斜边的直角三角形？

查看试题解析
18. 如图，在菱形ABCD中，m、n、t分别是菱形ABCD的两条对角线长和边长，这时我们把关于x的形如“mx²+2 $\sqrt{2}$ tx+n=0”的元二次方程称为“菱系一元二次方程”。请解决下列问题：

(1)、填空：
①当m=6，n=8时，t=

②用含m，n的代数式表示t²值，t²=

(2)、求证：关于x的“菱系一元二次方程” mx²+2 $\sqrt{2}$ tx+n=0必有实数根：

(3)、若x=-1是“菱系一元二次方程”mx²+2 $\sqrt{2}$ tx+n=0的一个根，且菱形的面积是25，BE是菱形ABCD的AD边上的高，求BE的值。

查看试题解析

【培优版】北师大版数学九上2.3用公式法解一元二次方程 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学九上2.3用公式法解一元二次方程同步练习