【培优版】北师大版数学八上第三章位置与坐标单元测试卷

试卷更新日期：2024-07-17 类型：单元试卷

进入出卷网下载

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 平面直角坐标系中，点 $A (- 1 ， 4)$ ， $B (3 ， 1)$ ，经过点 $A$ 的直线 $a / / x$ 轴，点 $C$ 是直线 $a$ 上的一个动点，当线段 $B C$ 的长度最短时，点 $C$ 的坐标为（）

A、 $(- 1 ， 1)$ B、 $(4 ， 3)$ C、 $(3 ， 4)$ D、 $(3 ， - 1)$

查看试题解析
2. 已知点P（1+m，2m+1）在y轴上，点Q（6-2n，4+n）在x轴上，则点M（m，n）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，在平面直角坐标系中，长方形ABCD的顶点坐标分别为A(-1，2)，B(-1，-1)，C(1，-1)，D(1，2)，点P从点A出发，沿长方形的边顺时针运动，速度为每秒2个单位长度，点Q从点A出发，沿长方形的边逆时针运动，速度为每秒3个单位长度．记P，Q在长方形边上第1次相遇时的点为M₁ ，第二次相遇时的点为M₂ ，第三次相遇时的点为M₃ ， …，则点M₂₀₂₂的坐标为（）

A、(1，0) B、(-1，0) C、(1，2) D、(0，-1)

查看试题解析
4. 若 $| 3 x - 2 y - 1 | + \sqrt{x + y - 2} = 0$ ，则点（x，y）在第（）象限．

A、四 B、三 C、二 D、一

查看试题解析
5. 如图，在△ABC中，点A的坐标为（0，1），点B的坐标为（0，4），点C的坐标为（4，3），如果要使△ABD与△ABC全等，那么点D的坐标是（　　）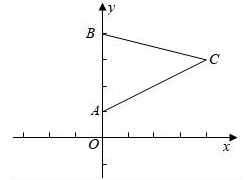

A、（﹣4，3） B、（﹣4，2） C、（4，2）或（﹣4，3） D、（4，2）或（﹣4，2）或（﹣4，3）

查看试题解析
6. 在平面直角坐标系中，下列说法：
①若点A（a，b）在坐标轴上，则ab=0；②若m为任意实数，则点（2，m²）一定在第一象限；③若点P到x轴的距离与到y轴的距离均为2，则符合条件的点P有2个；④已知点M（2，3），点N（-2，3），则MN∥x轴．其中正确的是（　　）

A、①④ B、②③ C、①③④ D、①②④

查看试题解析
7. 如图，在直角坐标系中，有若干个横、纵坐标分别为整数的点，其顺序按图中．“→方向排序，如（1，0）→（2，0）→（2，1）→（1，1）→（1，2）→（2，2） ……根据这个规律，第2020个点的横坐标为（）

A、44． B、45． C、46． D、47．

查看试题解析
8. 自然界中存在许多斐波那契螺旋线图案．斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数1，1，2，3，5，8，13，……画出螺旋曲线．在平面直角坐标系中，依次以这组数为半径作90°的圆弧 $\overset{⌢}{P_{1} P_{2}}$ ， $\overset{⌢}{P_{2} P_{3}}$ ， $\overset{⌢}{P_{3} P_{4}}$ ， …，得到一组螺旋线，连接 $P_{1} P_{2}$ ， $P_{2} P_{3}$ ， $P_{3} P_{4}$ ， …，得到一组螺旋折线，如图所示．已知点 $P_{1}$ ， $P_{2}$ ， $P_{3}$ 的坐标分别为 $(- 1 ， 0)$ ， $(0 ， 1)$ ， $(1 ， 0)$ ，则点 $P_{7}$ 的坐标为（）

A、 $(6 ， 1)$ B、 $(8 ， 0)$ C、 $(8 ， 2)$ D、 $(9 ， - 2)$

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. 在平面直角坐标系中，若点 $P (m + 3 ， 3 - m)$ 在y轴上，则m的值是.

查看试题解析
10. 在平面直角坐标系xOy中，点A（﹣4，0），B（2，0）在x轴上，若点P到两坐标轴的距离相等，且∠APO＝∠BPO ，则点P的坐标为．

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ ，我们把 $P^{'} (- y + 1 ， x + 1)$ 叫做点 P的伴随点，已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ … ，这样依次得到点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， … ， $A_{n}$ …若点 $A_{1}$ 的坐标为 $(4 ， 3)$ ，则点 $A_{2023}$ 的坐标为．

查看试题解析
12. 如图，A（4，0），B（0，6），若AB=BC，∠ABC=90°，则C点的坐标为

查看试题解析
13. 如图，在平面直角坐标系 $x O y$ 中， $△ A B C$ 的三个顶点的坐标分别是 $A (- 1 ， 0) ， B (1 ， 0) ， C (1 ， 2)$ ．点P到 $△ A B C$ 的距离定义如下：点Q为 $△ A B C$ 三边上的动点，当 $P Q$ 最小时，我们称此时 $P Q$ 的长度为点P到 $△ A B C$ 的距离，记为 $d (P ， △ A B C)$ ．已知矩形 $D E F G$ 的四个顶点依次是 $D (- 2 ， 3) ， E (- 2 ， - 2) ， F (2 ， - 2) ， G (2 ， 3)$ ，若点P在矩形 $D E F G$ 的四条边上，则满足 $d (P ， △ A B C) = \sqrt{2}$ 的点P有个．

查看试题解析

三、解答题（共7题；共61分）

14. 已知 $A (- 3 ， 0)$ ， $B (5 ， 0)$ ， $C (x ， y)$ ．

(1)、若点 $C$ 在第二象限内，且 $| x | = 3$ ， $| y | = 3$ ，求点 $C$ 的坐标，并求 $Δ A B C$ 的面积；

(2)、若点 $C$ 在第四象限内，且 $Δ A B C$ 的面积为8， $| x | = 4$ ，求点 $C$ 的坐标．

查看试题解析
15. 如图，△ABC的顶点都在6×6正方形网格纸的格点上，且A(-2，1)，B(-1，3)，C(0，2).按要求完成下列问题：

(1)、在坐标系中，描出点D(-2，-1)，E(-1，-3)，F(0，-2)的位置，并连接DE，EF，DF，则△ABC与△DEF关于对称；(填“x轴”或“y轴”)

(2)、画出△DEF关于y轴对称的△D'E'F'；

(3)、设点P是x轴上一动点，直接写出PA+PB的最小值.

查看试题解析
16. 如图，在平面直角坐标系中，设一点 $M$ 自 $P_{0} (1 ， 0)$ 处向上运动1个单位长度至 $P_{1} (1 ， 1)$ ，然后向左运动2个单位长度至 $P_{2}$ 处，再向下运动3个单位长度至 $P_{3}$ 处，再向右运动4个单位长度至 $P_{4}$ 处，再向上运动5个单位长度至 $P_{5}$ 处，…，如此继续运动下去，设 $P_{n} (x_{n} ， y_{n})$ ， $n = 1 ， 2 ， 3$ .

(1)、计算 $x_{1} + x_{2} + x_{3} + x_{4}$ .

(2)、计算 $x_{1} + x_{2} + \cdot \cdot \cdot + x_{2023} + x_{2024}$ 的值.

查看试题解析
17. 在平面直角坐标系 $x O y$ 中，对于 $P$ ， $Q$ 两点给出如下定义：若点 $P$ 到 $x$ 、 $y$ 轴的距离中的最大值等于点 $Q$ 到 $x$ 、 $y$ 轴的距离中的最大值，则称 $P$ ， $Q$ 两点为“等距点”．如图中的 $P$ ， $Q$ 两点即为“等距点”．
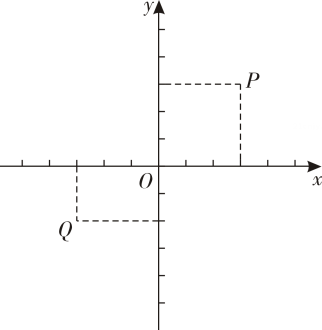
备用图

(1)、已知点 $A$ 的坐标为 $(- 3 ， 1)$ ，在点 $E (0 ， 3)$ ， $F (3 ， - 3)$ ， $G (2 ， - 5)$ 中，为点 $A$ 的“等距点”的是．

(2)、若 $T_{1} (- 1 ， - k - 3)$ ， $T_{2} (4 ， 4 k - 3)$ 两点为“等距点”，且两点纵坐标异号，求 $k$ 的值．

查看试题解析
18. 定义：在平面直角坐标系中，对于任意两点 $A (a ， b)$ ， $B (c ， d)$ ，若点 $T (x ， y)$ 满足 $x = \frac{a + c}{3}$ ， $y = \frac{b + d}{3}$ ，那么称点 $T$ 是点 $A$ 和 $B$ 的衍生点.例如： $M (- 2 ， 5)$ ， $N (8 ， - 2)$ ，则点 $T (2 ， 1)$ 是点 $M$ 和 $N$ 的衍生点.已知点 $D (3 ， 0)$ ，点 $E (m ， m + 2)$ ，点 $T (x ， y)$ 是点 $D$ 和 $E$ 的衍生点.

(1)、若点 $E (4 ， 6)$ ，则点 $T$ 的坐标为

(2)、请直接写出点 $T$ 的坐标（用 $m$ 表示）；

(3)、若直线 $E T$ 交 $x$ 轴于点 $H$ ，当 $∠ D H T = 90 °$ 时，求点 $E$ 的坐标.

查看试题解析
19. 在平面直角坐标系 $x O y$ 中，点 $A (a, b)$ ， $B (c, d)$ ，若 $c - a = d - b \neq 0$ ，则称点 $A$ 与点 $B$ 互为“等差点”，例如：点 $A (- 1, 3)$ ，点 $B (2, 6)$ ，因为 $2 - (- 1) = 6 - 3 \neq 0$ ，所以点 $A$ 与点 $B$ 互为“等差点”．

(1)、若点 $A$ 的坐标是 $(4, - 2)$ ，则在点 $B_{1} (2, 0)$ ， $B_{2} (- 1, - 7)$ ， $B_{3} (0, - 6)$ 中，点 $A$ 的“等差点”为点；

(2)、若点 $A$ 的坐标是 $(5, - 3)$ 的“等差点” $B$ 在坐标轴上，求点 $B$ 的坐标；

(3)、若点 $A$ 的坐标是 $(- \sqrt{3}, 2 m)$ 与点 $B (2 \sqrt{3}, - n)$ 互为“等差点”，且 $m$ 、 $n$ 互为相反数，求点 $B$ 的坐标．

查看试题解析
20. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

(1)、实验与探究：
观察图，易知A(0，2)关于直线l的对称点 $A$ 的坐标为(2，0)，请在图中分别标明B(5，3)、C(﹣2，5)关于直线l的对称点 $B$ 、 $C$ 的位置，并写出他们的坐标： $B$ ， $C$ ；

(2)、归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a，b)关于第一、三象限的角平分线l的对称点 $P$ 的坐标为（不必证明）；

(3)、运用与拓广：已知两点D(1，﹣3)、E(﹣3，﹣4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小．

查看试题解析

【培优版】北师大版数学八上第三章位置与坐标 单元测试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题（共7题；共61分）

【培优版】北师大版数学八上第三章位置与坐标单元测试卷