【培优版】北师大版数学八上 3.2平面直角坐标系 同步练习
试卷更新日期:2024-07-17 类型:同步测试
一、选择题
-
1. 无论m取什么实数,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在平面直角坐标系中,对于点 , 若点坐标为其中为常数,且 , 则称点是点的“属派生点”例如,点的“属派生点”为 , 即若点的“属派生点是点 , 则点的坐标为( )A、 B、 C、 D、3. 已知点 , 其中a , b均为实数,若a , b满足 , 则称点A为“和谐点”.若点是“和谐点”,则点B在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是( )
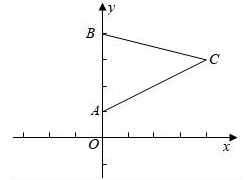 A、(﹣4,3) B、(﹣4,2) C、(4,2)或(﹣4,3) D、(4,2)或(﹣4,2)或(﹣4,3)5. 点坐标为 , 且点到两坐标轴的距离相等,则点的坐标是( )A、 B、 C、或 D、或6. 如图,已知四边形ABCD的顶点为 , , , , 点M和点N同时从点出发作顺时针运动,点M的速度为1个单位每秒,点N的速度为4个单位每秒,那么点N第2024次追上点M时的坐标为( )
A、(﹣4,3) B、(﹣4,2) C、(4,2)或(﹣4,3) D、(4,2)或(﹣4,2)或(﹣4,3)5. 点坐标为 , 且点到两坐标轴的距离相等,则点的坐标是( )A、 B、 C、或 D、或6. 如图,已知四边形ABCD的顶点为 , , , , 点M和点N同时从点出发作顺时针运动,点M的速度为1个单位每秒,点N的速度为4个单位每秒,那么点N第2024次追上点M时的坐标为( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( ) A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)8. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(4,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以6个单位秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( )
A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)8. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(4,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以6个单位秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( ) A、(0,2) B、(﹣4,0) C、(0,﹣2) D、(4,0)
A、(0,2) B、(﹣4,0) C、(0,﹣2) D、(4,0)二、填空题
-
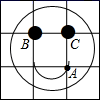
9. 点在第三象限,到轴的距离为3,则它到轴的距离为 .10. 将如图所示的“ ”笑脸放置在 的正方形网格中, 、 、 三点均在格点上.若 、 的坐标分别为 , ,则点 的坐标为.
 11. 如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a﹣3),则a的值为 .
11. 如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a﹣3),则a的值为 .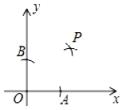 12. 如图,A(4,0),B(0,6),若AB=BC,∠ABC=90°,则C点的坐标为
12. 如图,A(4,0),B(0,6),若AB=BC,∠ABC=90°,则C点的坐标为 13. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为.
13. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为.
三、解答题
-
14. 如图
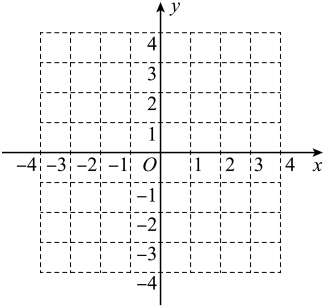 (1)、在平面直角坐标系中,画 , 使其三个顶点为 , , ;(2)、是直角三角形吗?请证明你的判断.15. 如图,在 中, , ,点 的坐标为 ,点 的坐标为 ,求点 的坐标.
(1)、在平面直角坐标系中,画 , 使其三个顶点为 , , ;(2)、是直角三角形吗?请证明你的判断.15. 如图,在 中, , ,点 的坐标为 ,点 的坐标为 ,求点 的坐标. 16. 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a﹣3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.
16. 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a﹣3)2+|b+4|=0,S四边形AOBC=16,求C点坐标. 17. 在平面直角坐标系中.(1)、已知点P(2a-6,a+4)在y轴上,求点P的坐标;(2)、已知两点A(-3,m-1),B(n+1,4)若AB∥x 轴,点B在第一象限,求m的值,并确定n的取值范围;
17. 在平面直角坐标系中.(1)、已知点P(2a-6,a+4)在y轴上,求点P的坐标;(2)、已知两点A(-3,m-1),B(n+1,4)若AB∥x 轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)、在(1)(2)的条件下,如果线段 AB 的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.18. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在中, , , 线段经过点C,且于点D,于点E.求证: , ”这个问题时,只要证明 , 即可得到解决, (1)、积累经验:
(1)、积累经验:请写出证明过程;
(2)、类比应用:如图2,在平面直角坐标系中,中, , , 点A的坐标为 , 点C的坐标为 , 求点B与x轴的距离.
 (3)、拓展提升:
(3)、拓展提升:如图3,在平面直角坐标系中, , , 点A的坐标为 , 点C的坐标为 , 求点B的坐标.
