【培优版】北师大版数学八上第二章实数单元测试卷

试卷更新日期：2024-07-17 类型：单元试卷

进入出卷网下载

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 下列说法正确的有（　　）个．
①任何实数都可以开立方；②0的相反数、倒数、平方都是0；③数轴上的点和有理数一一对应；④有限小数和无限循环小数都是有理数；⑤无理数都是无限小数．

A、1 B、2 C、3 D、4

查看试题解析
2. 计算 $\sqrt{8} + \sqrt{18}$ 的结果是（）

A、 $\sqrt{26}$ B、 $2 \sqrt{5}$ C、 $5 \sqrt{2}$ D、 $7 \sqrt{2}$

查看试题解析
3. 若 $a = \sqrt{2 b - 4} + \sqrt{4 - 2 b} - 1$ ，则 $a + b$ 的值为（）

A、1 B、0 C、 $- 1$ D、2

查看试题解析
4. 已知 $\sqrt{\frac{1 - a}{a^{2}}} = \frac{\sqrt{1 - a}}{4}$ ，则 $a$ 的值是（）

A、 $a = 1$ B、 $a = - 1$ C、 $a = 4$ D、 $a = - 4$

查看试题解析
5. 若 $x = 3 - \sqrt{2023}$ ，则代数式x²-6x-8的值是(　　)

A、2006 B、2005 C、2004 D、2003

查看试题解析
6. 如图，面积为6的正方形ABCD的顶点A在数轴上，且表示的数为﹣1，若点E在数轴上，（点E在点A的右侧）且AB＝AE ，则点E所表示的数为（　　）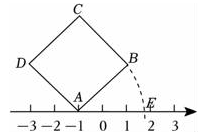

A、 $\sqrt{6} - 1$ B、 $\sqrt{6}$ C、 $\sqrt{6} + 1$ D、 $\sqrt{6} + 2$

查看试题解析
7. 若 $a_{n} = 1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}$ （n为正整数），则下列说法正确的个数是（　　）
① ${\sqrt{a}}_{1} = 1 \frac{1}{2} ， \sqrt{a_{2}} = 1 \frac{1}{6} ， \sqrt{a_{3}} = 1 \frac{1}{12}$ ；
② $\sqrt{a_{4}} = 1 + \frac{1}{4} - \frac{1}{5}$ ；
③ $\sqrt{a_{1}} + \sqrt{a_{2}} + \sqrt{a_{3}} + ⋯ + \sqrt{a_{8}} = 8 \frac{8}{9}$ ．

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 观察下列二次根式的化简
S₁= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2}$
S₂= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = (1 + \frac{1}{1} - \frac{1}{2}) + (1 + \frac{1}{2} - \frac{1}{3})$
S₃= $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = (1 + \frac{1}{1} - \frac{1}{2}) + (1 + \frac{1}{2} - \frac{1}{3}) + (1 + \frac{1}{3} - \frac{1}{4})$ ，则 $\frac{S_{2023}}{2023}$ =（）

A、 $\frac{1}{2022}$ B、 $\frac{2022}{2021}$ C、 $\frac{2024}{2023}$ D、 $\frac{2025}{2024}$

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. 函数 $y = \sqrt{x + 3}$ 中，自变量x的取值范围是．

查看试题解析
10. 若实数 $\sqrt{7}$ 的小数部分为a ，则 $a =$ ．

查看试题解析
11. 若实数 $a = \frac{1}{2 - \sqrt{3}}$ ，则代数式 $a^{2} - 4 a + 4$ 的值为.

查看试题解析
12. 化简二次根式 $a \sqrt{- \frac{a + 2}{a^{2}}}$ 的结果是.

查看试题解析
13. 已知a、b是正整数，如果有序数对(a, b)能使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的值也是整数，那么称（a,b）是2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的一个“理想数对”。如（1，1）使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ =4，（4，4）使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 所以（1,1）和（4，4）都是2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的“理想数对”，请你再写出一个2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的“理想数对”： .

查看试题解析

三、解答题（共7题；共61分）

14. 有理数a、b、c在数轴上的位置如图所示，化简 $\sqrt{{(a - b)}^{2}} - | b + c | - \sqrt{{(b - c)}^{2}}$

查看试题解析
15.

(1)、设a、b、c、d为正实数，a＜b，c＜d，bc＞ad，有一个三角形的三边长分别为 $\sqrt{a^{2} + c^{2}}$ ， $\sqrt{b^{2} + d^{2}}$ ， $\sqrt{{(b - a)}^{2} + {(d - c)}^{2}}$ ，求此三角形的面积；

(2)、已知a，b均为正数，且a+b=2，求U= $\sqrt{a^{2} + 4} + \sqrt{b^{2} + 1}$ 的最小值．

查看试题解析
16. 小丽根据学习“数与式”积累的经验，想通过“由特殊到一般”的方法探究下面二次根式的运算规律．
下面是小丽的探究过程，请补充完整：

(1)、具体运算，发现规律，
特例1： $\sqrt{1 + \frac{1}{3}} = \sqrt{\frac{3 + 1}{3}} = \sqrt{4 \times \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$
特：2： $\sqrt{2 + \frac{1}{4}} = \sqrt{\frac{8 + 1}{4}} = \sqrt{9 \times \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$
特：3： $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$
特例4：．（填写一个符合上述运算特征的例子）；

(2)、观察、归纳，得出猜想．
如果n为正整数，用含n的式子表示上述的运算规律为：；

(3)、证明你的猜想；

(4)、应用运算规律化简： $\sqrt{2022 + \frac{1}{2024}} \times \sqrt{4048}$ ＝．

查看试题解析
17. 阅读下面的文字，解答问题： $\sqrt{2}$ 是一个无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分无法全部写出来，但是我们可以想办法把它表示出来因为 $1 < \sqrt{2} < 2$ ，所以 $\sqrt{2}$ 的整数部分为1，将 $\sqrt{2}$ 减去其整数部分后，得到的差就是小数部分，于是 $\sqrt{2}$ 的小数部分为 $\sqrt{2} - 1$ ．请解答下列问题：

(1)、 $\sqrt{5}$ 的整数部分是，小数部分是；

(2)、如果 $7 + \sqrt{10}$ 的小数部分为a， $7 - \sqrt{10}$ 的小数部分为b，若 $(x + 1)^{2} = a + b$ ，求x的值．

查看试题解析
18. 阅读下面内容：
（ 1 ） $\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；

（ 2 ） $\frac{1}{\sqrt{3} - \sqrt{2}} = \frac{1 \times (\sqrt{3} + \sqrt{2})}{(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2})} = \sqrt{3} + \sqrt{2}$ ；

(1)、计算：① $\frac{1}{\sqrt{7} + \sqrt{6}}$ ；② $\frac{4}{\sqrt{13} - 3}$ ；

(2)、计算下列式子的值：
$(\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{2001} + \sqrt{2002}} + \frac{1}{\sqrt{2002} + \sqrt{2003}}) (1 + \sqrt{2003})$

查看试题解析
19. 小明在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²﹣8a+1的值，他是这样分析与解答的：
∵a＝ $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．
∴a﹣2＝﹣ $\sqrt{3}$ ．
∴(a﹣2)²＝3，即a²﹣4a+4＝3．
∴a²﹣4a＝﹣1，
∴2a²﹣8a+1＝2(a²﹣4a)+1＝2×(﹣1)+1＝﹣1．
请你根据小明的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1}$ ＝　　；

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2020} + \sqrt{2019}}$ ；

(3)、若a＝ $\frac{1}{\sqrt{5} - 2}$ ，求2a²﹣8a+1的值．

查看试题解析
20. 如果一个三角形的三边长分别为a ， b ， c ，记 $p = \frac{a + b + c}{2}$ ，那么三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ . $①$
古希腊的几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中，给出了公式 $①$ 和它的证明，这一公式称为海伦公式.
我国南宋时期数学家秦九韶（约1202-1261），曾提出利用三角形的三边求面积的秦九韶公式
$S = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ . $②$

(1)、在 $△ A B C$ 中， $A B = 8$ ， $B C = 10$ ， $A C = 12$ ，利用上面公式 $①$ 求 $△ A B C$ 的面积；

(2)、求证： $\sqrt{p (p - a) (p - b) (p - c)} = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ .

查看试题解析

【培优版】北师大版数学八上第二章 实数 单元测试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题 （共7题；共61分）

【培优版】北师大版数学八上第二章实数单元测试卷

三、解答题（共7题；共61分）