【培优版】北师大版数学八上2.4估算同步练习

试卷更新日期：2024-07-17 类型：同步测试

进入出卷网下载

一、选择题

1. 设681×2019﹣681×2018=a ， 2015×2016﹣2013×2018=b ， $\sqrt{678^{2} + 1358 + 690 + 678} = c$ ，则a ， b ， c的大小关系是（）

A、b＜c＜a B、a＜c＜b C、b＜a＜c D、c＜b＜a

查看试题解析
2. 估计 $\sqrt{35}$ 的值（）

A、在 $6$ 和 $7$ 之间 B、在 $5$ 和 $6$ 之间 C、在 $3$ 和 $4$ 之间 D、在 $2$ 和 $3$ 之间

查看试题解析
3. 设 $\sqrt{13}$ 的小数部分为a ，则 $a^{2} + \sqrt{9} \times \sqrt{52}$ 的值为（）

A、22 B、 $13 - 6 \sqrt{13}$ C、 $4 - 6 \sqrt{13}$ D、 $4 + 6 \sqrt{13}$

查看试题解析
4. 估算 $8 - \sqrt{31}$ 的值在（）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
5. 设 $\sqrt{3}$ 的小数部分是 $m ， \sqrt{7}$ 的整数部分是 $n$ ，则 $(m + 1)^{n}$ 的值是（）

A、3 B、7 C、9 D、一个无理数

查看试题解析
6. 已知 $a$ ， $b$ 分别是 $7 - \sqrt{13}$ 的整数部分和小数部分，那么 $2 a - b$ 的值是（）

A、 $3 - \sqrt{13}$ B、 $4 - \sqrt{13}$ C、 $\sqrt{13}$ D、 $2 + \sqrt{13}$

查看试题解析
7. 已知44²＝1936，45²＝2025，46²＝2116，47²＝2209，若n为整数且n＜ $\sqrt{2170}$ ＜n＋1，则n的值为（）

A、44 B、45 C、46 D、47

查看试题解析
8. 如图1，在 $△ A B C$ 中， $A B = B C = 2$ ， $∠ B = 120 °$ ， M是 $B C$ 的中点，设 $A M = a$ ，则表示实数a的点落在数轴上（如图2）所标四段中的（）

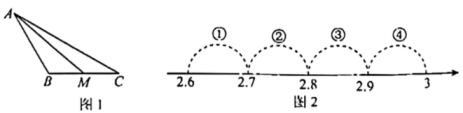A、①段 B、②段 C、③段 D、④段

查看试题解析

二、填空题

9. 若 $a = \sqrt{1003} + \sqrt{997}$ ， $b = \sqrt{1001} + \sqrt{999}$ ， $c = 2 \sqrt{1001}$ ，则 $a ， b ， c$ 的大小关系用“＜”号排列为．

查看试题解析
10. 阅读下列材料：因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以 $\sqrt{5}$ 的整数部分为 $2$ ，小数部分为 $\sqrt{5} - 2$ ，若规定实数 $m$ 的整数部分记为 $[m]$ ，小数部分记为 ${m}$ ，可得 $[\sqrt{5}] = 2$ ， ${\sqrt{5}} = \sqrt{5} - 2 .$ 按照此规定计 ${5 - \sqrt{5}}$ 的值是．

查看试题解析
11. 已知 $1 1^{3} = 1331 ， 1 2^{3} = 1728 ， 1 3^{3} = 2197 ， 1 4^{3} = 2744$ ．若 $n$ 为整数，且 $n < \sqrt[3]{2023} < n + 1$ 则 $n =$ ．

查看试题解析
12. 介于 $\sqrt{3} + 1$ 和 $\sqrt{11}$ 之间的整数是.

查看试题解析
13. 观察：观察 $\sqrt{5} = 2.236$ ， $\sqrt{50} = 7.071$ ， $\sqrt[3]{6.137} = 1.8308$ ， $\sqrt[3]{6137} = 18.308$ ；填空：
$①$ 则 $\sqrt{0.5} =$ ．
$②$ 若 $\sqrt[3]{x} = - 0.18308$ ，则 $x =$ ．

查看试题解析

三、解答题

14.

(1)、观察下列各式，并用所得到的规律解决问题：
① $\sqrt{0.07} \approx 0.2646$ ，则 $\sqrt{7} \approx 2.646 ， \sqrt{700} \approx 26.46 ⋯$
② $\sqrt[3]{1000000} = 100 ， \sqrt[3]{1000} = 10 ， \sqrt[3]{1} = 1 ⋯$
发现规律：①被开方数的小数点每向右移动两位，其算术平方根的小数点向移动位；
②被开方数的小数点每向左移动三位，其立方根的小数点向移动位；

(2)、应用：①已知 $\sqrt{0.03} \approx 0.1732 ， \sqrt{3} \approx$ ， $\sqrt{300} \approx$ ；
②已知 $\sqrt[3]{10} \approx 2.154 ， \sqrt[3]{a} \approx - 0.2154$ ，则 $a =$ ；

(3)、拓展：已知 $\sqrt{6} \approx 2.449 ， \sqrt{60} \approx 7.746$ ，计算 $\sqrt{240}$ 和 $\sqrt{0.54}$ 的值．

查看试题解析
15. 已知 $3 a + 2$ 的立方根是2， $3 a + b - 1$ 的算术平方根是4，c是 $\sqrt{8}$ 的整数部分.

(1)、求a、b、c的值；

(2)、求 $a + b - c$ 的平方根.

查看试题解析
16. 数学老师在课堂上提出一个问题：“通过探究知道： $\sqrt{2} \approx 1.414 \dots$ ，它是个无限不循环小数，也叫无理数，它的整数部分是 $1$ ，那么有谁能说出它的小数部分是多少？”，小明举手回答：它的小数部分我们无法全部写出来，但可以用 $\sqrt{2} - 1$ 来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法 $.$ 现请你根据小明的说法解答：

(1)、 $\sqrt{5}$ 的小数部分是 $a$ ， $\sqrt{13}$ 的整数部分是 $b$ ，求 $a + b - \sqrt{5}$ 的值．

(2)、已知 $8 + \sqrt{3} = x + y$ ，其中 $x$ 是一个整数， $0 < y < 1$ ，求 $3 x + (y - \sqrt{3})^{2018}$ 的值．

查看试题解析
17. 阅读下面的文字，解答问题.
无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来，比如π、 $\sqrt{2}$ 等，而常用“……”或者“≈”的表示方法都不够百分百准确，于是小刚用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小刚的表示方法吗？事实上，小刚的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分，又例如：因为 $\sqrt{4} ＜ \sqrt{5} ＜ \sqrt{9}$ ，即2＜ $\sqrt{5}$ ＜3，所以 $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ，也就是说，任何一个无理数，都可以夹在两个相邻的整数之间。根据上述信息，请回答下列问题：

(1)、 $\sqrt{21}$ 的整数部分是，小数部分是；

(2)、10+ $\sqrt{7}$ 也是夹在两个整数之间的，可以表示为 $a ＜ 10 + \sqrt{7} ＜ b$ ，则 $(a - b)_{}^{2013} =$ ；

(3)、若 $\sqrt{23} - 2 = x + y$ ，其中 $x$ 是整数，且0<y<1，求： $x - y$ 的相反数.

查看试题解析

四、实践探究题

18. 阅读材料：学习了无理数后，某数学兴趣小组开展了一次探究活动：估算 $\sqrt{13}$ 的近似值．
小明的方法：
∵ $\sqrt{9} < \sqrt{13} < \sqrt{16}$ ，设 $\sqrt{13} = 3 + k (0 < k < 1)$ ，
∴ ${(\sqrt{13})}^{2} = {(3 + k)}^{2}$ ． ∴ $13 ＝ 9 + 6 k + k^{2}$ ．
∴ $13 \approx 9 + 6 k$ ，解得 $k \approx \frac{2}{3}$ ． ∴ $\sqrt{13} \approx 3 + \frac{2}{3} \approx 3.67$ ．
（上述方法中使用了完全平方公式： $（ a + b ）^{2} ＝ a^{2} + 2 a b + b^{2}$ ，下面可参考使用）问题：

(1)、请你依照小明的方法，估算 $\sqrt{41}$ 的值（结果保留两位小数）；

(2)、请结合上述具体实例，概括出估算 $\sqrt{m}$ 的公式：已知非负整数a、b、 $a ＜ \sqrt{m} ＜ a + 1$ ，且 $m ＝ a^{2} + b$ ，估计 $\sqrt{m}$ 的值（用含a、b的代数式表示）；

(3)、请用（2）中的结论估算 $\sqrt{37}$ 的近似值．

查看试题解析

【培优版】北师大版数学八上2.4估算 同步练习

一、选择题

二、填空题

三、解答题

四、实践探究题

【培优版】北师大版数学八上2.4估算同步练习