【提升版】北师大版数学八上2.4估算同步练习

试卷更新日期：2024-07-17 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在平面直角坐标系中，已知点O(0，0)，A(2，3)，以点O为圆心，OA长为半径画弧，交x轴的正半轴于B点，则B点的横坐标介于（）

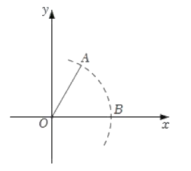A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
2. 大、中、小三个正方形摆放如图所示，若大正方形的面积为5，小正方形的面积为1，则中正方形 $A B C D$ 的边长可能是（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、3

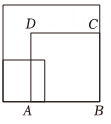查看试题解析
3. 如图所示，下列选项中，被污渍覆盖住的无理数可能是（）

A、 $- \sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{11}$ D、 $\sqrt{17}$

查看试题解析
4. 小明利用计算器得到下表中的数据：
$x$
8
8.5
9
9.5
10
$x^{2}$
64
72.25
81
90.25
100
$x^{3}$
512
614.125
729
857.375
1000
那么 $\sqrt[3]{888}$ 在（）之间

A、 $9.0 ~ 9.5$ B、 $9.5 ~ 10$ C、 $90 ~ 95$ D、 $95 ~ 100$

查看试题解析
5. 秦兵马俑的发现被誉为“世界第八大奇迹”，兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 $\frac{\sqrt{5} - 1}{2}$ ，请你估算 $\sqrt{5} - 1$ 的值（）

A、在0和1之间 B、在1和2之间 C、在2和3之间 D、在3和4之间

查看试题解析
6. 已知 $\sqrt[3]{326} \approx 6.882$ ，若 $\sqrt[3]{x} \approx 68.82$ ，则x的值约为（）

A、326000 B、32600 C、3.26 D、0.326

查看试题解析
7. 学习了无理数之后，对于 $\sqrt{14}$ ，下列说法正确的是（）
I： $\sqrt{14}$ 表示的意义是14的算术平方根； II：面积是14的正方形边长是 $\sqrt{14}$ ；
III： $\sqrt{14}$ 的大小界于两个连续整数3与4之间.

A、三个都正确 B、只有I与II正确 C、只有II与III正确 D、只有II不对

查看试题解析
8. 如图，小明学了在数轴上画出表示无理数的点的方法后，进行练习：首先画数轴，原点为 $O$ ，在数轴上找到表示数 $2$ 的点 $A$ ，然后过点 $A$ 作 $A B ⊥ O A$ ，使 $A B = 3 ($ 如图 $) .$ 以 $O$ 为圆心， $O B$ 长为半径作弧，交数轴正半轴于点 $P$ ，则点 $P$ 所表示的数介于（）

A、 $1$ 和 $2$ 之间 B、 $2$ 和 $3$ 之间 C、 $3$ 和 $4$ 之间 D、 $4$ 和 $5$ 之间

查看试题解析

二、填空题

9. 若 $\sqrt{19}$ +1的值在两个整数a与a+1之间，则a= ．

查看试题解析
10. 规定用符号 $[m]$ 表示一个实数 $m$ 的整数部分，例如 $[0.6] = 0$ ， $[3.14] = 3$ ，按此规定 $[\sqrt{10} + 2]$ 的值为．

查看试题解析
11. 设 $x$ 表示 $\sqrt{5}$ 的整数部分， $y$ 表示它的小数部分，求 $(\sqrt{5} + x) y =$ .

查看试题解析
12. 如图，用边长为3的两个小正方形拼成一个大正方形，则大正方形的边长最接近的整数是．

查看试题解析

三、解答题

13. 现规定：分别用 $[x]$ 和 $⟨ x ⟩$ 表示实数 $x$ 的整数部分和小数部分，如实数3.14的整数部分是 $[3.14] = 3$ ，小数部分是 $⟨ 3.14 ⟩ = 0.14$ ；实数 $\sqrt{7}$ 的整数部分是 $[\sqrt{7}] = 2$ ，小数部分是无限不循环小数，无法写完整，但是把它的整数部分减去，就等于它的小数部分，即 $\sqrt{7} - 2$ 就是 $\sqrt{7}$ 的小数部分，所以 $⟨ \sqrt{7} ⟩ = \sqrt{7} - 2$ ．

(1)、 $[\sqrt{2}] =$ ， $⟨ \sqrt{2} ⟩ =$ ， $[\sqrt{11}] =$ ， $⟨ \sqrt{11} ⟩ =$ ；

(2)、如果 $⟨ \sqrt{5} ⟩ = a$ ， $[\sqrt{101}] = b$ ，求 $a + b - \sqrt{5}$ 的立方根．

查看试题解析
14. 如图，每个小正方形的边长均为1．

(1)、图中阴影部分的面积是；阴影部分正方形的边长 $a$ 是．

(2)、估计边长 $a$ 的值在两个相邻整数与之间．

(3)、我们知道 $π$ 是无理数，而无理数是无限不循环小数，因此 $π$ 的小数部分我们不可能全部写出来，用 $(π - 3)$ 表示它的小数部分．设边长 $a$ 的整数部分为 $x$ ，小数部分为 $y$ ，求 $x - y$ 的值．

查看试题解析
15. 已知a、b为有理数，m、n分别表示 $6 - \sqrt{13}$ 的整数部分和小数部分，且 $a m + b n = 6 + \sqrt{13}$ ，求 $2 a - 8 b$ 的平方根．

查看试题解析
16. 我们知道 $\sqrt{2}$ 是无理数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如： $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以 $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ ．
请根据以上信息，回答下列问题：

(1)、 $\sqrt{34}$ 整数部分是，小数部分是；

(2)、如果 $\sqrt{11}$ 的整数部分为 $a ， \sqrt{17}$ 的整数部分为 $b$ ，求 $12 a + 7 b$ 的立方根；

(3)、已知 $9 - \sqrt{7} = x - y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，求 $x + y$ 的值．

查看试题解析

$x$	8	8.5	9	9.5	10
$x^{2}$	64	72.25	81	90.25	100
$x^{3}$	512	614.125	729	857.375	1000

【提升版】北师大版数学八上2.4估算 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学八上2.4估算同步练习