【基础版】新北师大版(2024)数学七上第三章整式及其加减单元测试卷

试卷更新日期：2024-07-16 类型：单元试卷

进入出卷网下载

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 下列代数式中，是次数为3的单项式的是（）

A、 $- m^{3} n$ B、3 C、 $4 t^{3} - 3$ D、 $\frac{x^{2} y}{2}$

查看试题解析
2. 下列说法正确的是（）

A、0不是单项式 B、 $x^{2} y$ 的系数是0，次数是2 C、 $- \frac{π x^{2}}{3}$ 的系数是 $- \frac{1}{3}$ D、 $- a b c$ 的系数是 $- 1$ ，次数是3

查看试题解析
3. 如图所示，边长为 $a$ 的正方形中阴影部分的面积为（）

A、 $a^{2} - π {(\frac{a}{2})}^{2}$ B、 $a^{2} - π a^{2}$ C、 $a^{2} - π a$ D、 $a^{2} - 2 π a$

查看试题解析
4. 下列各式： $m$ ， $- \frac{1}{3} a b$ ， $\frac{1}{b}$ ， $\frac{y - x}{2}$ ， $m^{2} - 4 m + 3$ ， $\frac{x^{2} - 2 y}{π}$ ， $3$ ， $y^{3} - 3 y + \frac{1}{y}$ 中，整式有（）

A、7个 B、6个 C、4个 D、3个

查看试题解析
5. 一个长方形的周长为 $14 m + 6 n$ ，其中一边的长为 $3 m + 2 n$ ，则另一边的长为 $($ 　　 $)$

A、 $4 m + n$ B、 $7 m + 3 n$ C、 $11 m + 4 n$ D、 $8 m + 2 n$

查看试题解析
6. 如图，把四张形状大小完全相同的小长方形卡片(如图1)，不重叠地放在一个长为 $a c m$ 、宽为 $b c m$ 长方形内(如图2)，未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长和是（）

A、 $4 a c m$ B、 $4 b c m$ C、 $2 (a + b) c m$ D、 $4 (a - b) c m$

查看试题解析
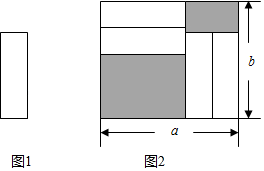7. 观察下列“蜂窝图”，按照这样的规律，则第2023个图案中的“”的个数是 $($ 　　 $)$

A、6074 B、6072 C、6070 D、6068

查看试题解析
8. 若 $A = x^{2} y + 2 x + 3 ， B = - 2 x^{2} y + 4 x$ ，则 $2 A - B =$ （）．

A、3 B、6 C、 $4 x^{2} y + 6$ D、 $4 x^{2} y + 3$

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. 单项式 $2 a^{2} b$ 的次数是．

查看试题解析
10. 如果单项式 $5 x^{m} y$ 与 $- 3 x^{2} y^{n}$ 是同类项，那么 $m + n =$ ．

查看试题解析
11. 多项式 $\frac{5 x^{2} - 2}{7}$ 的常数项是．

查看试题解析
12. 为了帮助地震灾区重建家园，某班全体师生积极捐款，捐款金额共3150元，其中5名教师人均捐款a元，则该班学生共捐款元（用含有a的代数式表示）．

查看试题解析
13. 某种商品原价是每件a元，商店老板为了增加销量，减少库存，第一次降价打“八折”，第二次降价每一件又减8元．两次降价后的每件售价是元．

查看试题解析

三、解答题（共7题；共61分）

14. 代数式：①-x；②x²+x-1；③ $\frac{n}{m}$ ；④ $\frac{m}{2} + 1$ ；⑤ $- \frac{1}{2}$ ；⑥πm³y；⑦ $\sqrt{m}$ ；⑧ $\frac{m + n}{2}$ ．

(1)、请上述代数式的序号分别填在相应的圆圈内：

(2)、其中次数最高的多项式是次项式；

(3)、其中次数最高的单项式的次数是，系数是．

查看试题解析
15. 整式加减：

(1)、整式化简： $2 (a^{2} b - a b^{2}) - 2 (a^{2} b + 1) + 2 a b^{2} - 2$ ．

(2)、先化简，再求值： $7 a^{2} b + (- 4 a^{2} b + 2 a b) - (2 a b + 2 a^{2} b)$ ，其中 $a = - 2$ ， $b = 1$ ．

查看试题解析
16. 已知多项式 $A$ 与多项式 $B$ 的和为 $12 x^{2} y + 2 x y + 5$ ，其中 $B = 3 x^{2} y - 5 x y + x + 7$ .

(1)、求多项式 $A$ .

(2)、当 $x$ 取任意值时，式子 $2 A - (A + 3 B)$ 的值是一个定值，求 $y$ 的值.

查看试题解析
17.

(1)、化简： $a^{2} b - [7 (\frac{1}{2} a b^{2} - a^{2} b) - \frac{3}{2} (a b^{2} - 8 a^{2} b)]$ ；

(2)、若（Ⅰ）中的 $a$ 是 $\frac{2}{3}$ 的相反数，且 $a$ 与 $b$ 互为倒数，求（Ⅰ）中代数式的值．

查看试题解析
18. 如图，一个大立方体由若干大小相同的小立方体组成．若原大立方体的体积为27a³ ，切去一部分后，剩下部分的体积为多少？

查看试题解析
19. 2023年10月26日，“神州十七号”飞船成功出征太空.同学们倍受鼓舞，某同学绘制了如图所示的火箭模型截面图，上面是三角形，中间是长方形，下面是梯形.

(1)、用含有x，y的代数式表示该截面的面积S；

(2)、当x=3，y=2时，求这个截面的面积.

查看试题解析
20. 某销售办公用品的商店推出两种优惠方案：
①购买一个书包，赠送一支水性笔；②书包和水性笔一律按九折优惠.

已知每个书包定价为20元，每支水性笔定价为5元.

(1)、若小明和同学需买4个书包，x支水性笔（不少于4支），请用含x的代数式表示两种优惠方案各需多少元.

(2)、当x = 20时，采用哪种方案更划算？

查看试题解析

【基础版】新北师大版(2024)数学七上第三章 整式及其加减 单元测试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题（共7题；共61分）

【基础版】新北师大版(2024)数学七上第三章整式及其加减单元测试卷