【提升版】新北师大版(2024)数学七上 3.3探索规律与表达同步练习

试卷更新日期：2024-07-16 类型：同步测试

进入出卷网下载

一、选择题

1. 按一定规律排列的代数式： $2 x$ ， $3 x^{2}$ ， $4 x^{3}$ ， $5 x^{4}$ ， $6 x^{5}$ ， $⋯$ ，第 $n$ 个代数式是（）

A、 $2 x^{n}$ B、 $(n - 1) x^{n}$ C、 $n x^{n + 1}$ D、 $(n + 1) x^{n}$

查看试题解析
2. 如图，将面积为1的长方形纸片分割成8个部分，部分①的面积是原长方形纸片面积的一半，部分②的面积是部分①面积的一半，部分③的面积是部分②面积的一半，依次类推，阴影部分的面积为（）

A、 $1 - \frac{1}{2^{7}}$ B、 $1 - \frac{1}{2^{8}}$ C、 $\frac{1}{2^{7}}$ D、 $\frac{1}{2^{8}}$

查看试题解析
3. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈， $⋅ ⋅ ⋅$ ，按此规律排列，则第⑨个图形中小圆圈的个数为（）

A、30 B、27 C、24 D、21

查看试题解析
4. 如图，黔西南州图书馆坐落于兴义市金笔路1号桔山广场旁，该图书馆把WIFI密码做成了数学题．小明在图书馆看书时，思索了一会儿，输入密码，顺利地连接到了“图书馆”的网络，那么他输入的密码是（　　）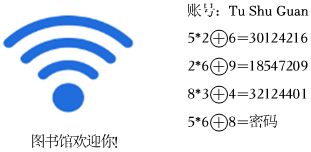

A、40138809 B、40488804 C、40138004 D、30488209

查看试题解析
5. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗；③中共有11颗星，图形①中共有17颗星，……，按此规律，图形⑦的颗数是（）

A、43 B、45 C、41 D、536

查看试题解析
6. 如图是用棋子摆成的图案，按照这样的规律摆下去，第⑨个图案需要的棋子个数为（）

A、 $81$ B、 $91$ C、 $109$ D、 $111$

查看试题解析
7. 如图是一个运算程序的示意图，若开始输入x的值为18，则第10次输出的结果为（）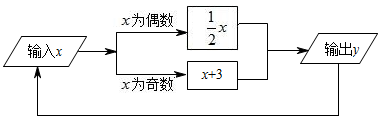

A、5 B、0 C、3 D、6

查看试题解析

二、填空题

8. 意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，请根据这组数的规律写出第10个数是．

查看试题解析
9. 用同样大小的黑色棋子按如图所示的方式摆放，按照这样的规律摆下去，用含n的代数式表示第n个图形需要棋子的枚数为．

查看试题解析
10. 下列图案是晋商大院窗格的一部分，其中“ $〇$ ”代表窗纸上所贴的剪纸．按此规律，则第10个图中所贴剪纸“ $〇$ ”的个数为．

查看试题解析

三、解答题

11. 【情景创设】
$\frac{1}{2} ， \frac{1}{6} ， \frac{1}{12} ， \frac{1}{20} ， \frac{1}{30}$ ，是一组有规律的数，我们如何求这些连续数的和呢？

(1)、【探索活动】根据规律第 $6$ 个数是， $\frac{1}{132}$ 是第个数，

(2)、【阅读理解】 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \frac{1}{5 \times 6} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} = 1 - \frac{1}{6}$
【实践应用】根据上面获得的经验完成下面的计算：
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + . . . + \frac{1}{132}$

(3)、 $\frac{1}{1 \times 2 \times 3} + \frac{1}{2 \times 3 \times 4} + \frac{1}{3 \times 4 \times 5} + . . . + \frac{1}{8 \times 9 \times 10}$

查看试题解析
12. 阅读材料：求1+2+2²+2³+2⁴+……+2²⁰¹⁹的值．
解：设S=1+2+2²+2³+2⁴+……+2²⁰¹⁹ ， ①
将等式①两边同时乘以2得：
2S=2+2²+2³+2⁴+2⁵……+2²⁰¹⁹+2²⁰²⁰ ． ②
将等式②与等式①两边分别相减得：
2S-S=2²⁰²⁰-1．
即： S=2²⁰²⁰-1．
∴1+2+2²+2³+2⁴+……=2²⁰²⁰-1．
请你仿照此法计算：

(1)、1+2+2²+2³+2⁴+……+2²⁰ ．

(2)、1+5+5²+5³+5⁴+……+5ⁿ ． (其中n为正整数)．

查看试题解析
13. 综合与探究
观察以下各式：
（x﹣y）（x+y）＝x²﹣y² ．
（x﹣y）（x²+xy+y²）＝x³﹣y³ ．
（x﹣y）（x³+x²y+xy²+y³）＝x⁴﹣y⁴ ．
（x﹣y）（x⁴+x³y+x²y²+xy³+y⁴）＝x⁵﹣y⁵ ．
请回答以下问题：

(1)、填空：（x﹣y）（x⁶+x⁵y+x⁴y²+x³y³+x²y⁴+xy⁵+y⁶）＝．

(2)、若n≥2，求证：6ⁿ﹣2ⁿ一定能被4整除．

(3)、求 $\frac{1 0^{20}}{9} -$ 10¹⁹﹣10¹⁸﹣10¹⁷﹣10¹⁶﹣…﹣10²﹣10﹣1的值．

查看试题解析

【提升版】新北师大版(2024)数学七上 3.3探索规律与表达 同步练习

一、选择题

二、填空题

三、解答题

【提升版】新北师大版(2024)数学七上 3.3探索规律与表达同步练习