【基础版】新北师大版(2024)数学七上 3.3探索与表达规律同步练习

试卷更新日期：2024-07-16 类型：同步测试

进入出卷网下载

一、选择题

1. 下列各正方形中的四个数之间都有相同的规律，根据此规律， $x$ 的值为（）

A、12 B、16 C、64 D、76

查看试题解析
2. 将一张长方形的纸对折，如图，对折1次可得到1条折痕（图中虚线），连续对折3次（对折时每次折痕与上次折痕保持平行），可以得到7条折痕；那么连续对折5次后，可以得到的折痕的条数是（）

A、31条 B、32条 C、33条 D、34条

查看试题解析
3. 已知下列一组数：1， $\frac{3}{4} ， \frac{5}{9} ， \frac{7}{16} ， \frac{9}{25}$ ，…；用代数式表示第n个数，则第n个数是（）

A、 $\frac{2 n - 1}{3 n - 2}$ B、 $\frac{2 n - 1}{n^{2}}$ C、 $\frac{2 n + 1}{3 n - 2}$ D、 $\frac{2 n + 1}{n^{2}}$

查看试题解析
4. 观察下列图形：
它们是按一定规律排列，依照此规律，第2023个图形中★的个数是（）

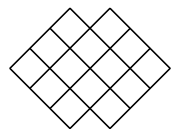
A、6067 B、6070 C、6073 D、6069

查看试题解析
5. 按一定规律排列的一列数依次是 $\frac{2}{3}$ 、1、 $\frac{8}{7}$ 、 $\frac{11}{9}$ 、 $\frac{14}{11}$ 、 $\frac{17}{13}$ …按此规律，这列数中第100个数是（）

A、 $\frac{299}{199}$ B、 $\frac{299}{201}$ C、 $\frac{301}{201}$ D、 $\frac{303}{203}$

查看试题解析
6. 根据图中数字的规律，则x+y的值是（）

A、729 B、550 C、593 D、738

查看试题解析
7. 下列图形都是由面积为1的正方形按一定的规律组成的，其中，第1个图形中面积为1的正方形有9个，第2个图形中面积为1的正方形有14个，……，按此规律，则第（）个图形中面积为1的正方形的个数为2024个．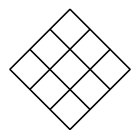

A、402 B、403 C、404 D、405

查看试题解析
8. 在某月的日历表中，竖列取连续的三个数字，它们的和可能是（）

A、18 B、38 C、75 D、33

查看试题解析

二、填空题

9. 将一列自然数按如图所示的规律排列， $A_{1}$ 表示的数为1， $A_{2}$ 表示的数为10， $A_{10}$ 表示的数为．

查看试题解析
10. 按一定规律排列的一列数依次为 $\frac{1}{2}$ ， - $\frac{1}{5}$ ， $\frac{1}{10}$ ， - $\frac{1}{17}$ ， $\frac{1}{26}$ ， - $\frac{1}{37}$ ， …，按此规律排列下去，这列数中第8个数是，第n个数是（n为正整数）．

查看试题解析
11. 观察下列一组数： $\frac{2}{3} ， \frac{6}{9} ， \frac{12}{27} ， \frac{20}{81} ， \frac{30}{243} ，$ ，它们是按一定规律排列的，那么这一组数的第n个数是.

查看试题解析
12. 观察下列图形：第1个图形有6根小棍，第2个图形有11根小棍，第3个图形有16根小棍，……，则第n(n为正整数)个图形中小棍共有根

查看试题解析
13. 观察下列单项式： $2 x$ ， $5 x^{2}$ ， $8 x^{3}$ ， $11 x^{4}$ ，…，则第n个式子是.

查看试题解析

三、解答题

14. 观察下面一列数：-1，2，-3，4，-5，6，-7，8，-9，……

(1)、请写出这一列数中的第100个数和第2022个数．

(2)、在前2022个数中，正数和负数分别有多少个？

(3)、2023和-2023是否都在这一列数中？若在，请指出它们分别是第几个数；若不在，请说明理由．

查看试题解析
15. 观察下列关于自然数的等式：
$3^{2} - 4 \times 1 = 4 + 1$ ， ①
$5^{2} - 4 \times 2 = 16 + 1$ ， ②
$7^{2} - 4 \times 3 = 36 + 1$ ， ③
……
根据上述规律解决下列问题.

(1)、写出第四个等式；

(2)、写出你猜想的第 $n$ 个等式.（用含 $n$ 的式子表示）

查看试题解析
16. 从2开始，连续的偶数相加，它们和的情况如下表：
加数的个数n
连续偶数的和S
1
$2 = 1 \times 2$
2
$2 + 4 = 6 = 2 \times 3$
3
$2 + 4 + 6 = 12 = 3 \times 4$
4
$2 + 4 + 6 + 8 = 20 = 4 \times 5$
5
$2 + 4 + 6 + 8 + 10 = 30 = 5 \times 6$

(1)、如果 $n = 8$ 时，那么S的值为；

(2)、由表中的规律猜想：用含n的代数式表示S的公式为 $S = 2 + 4 + 6 + ⋯ + 2 n =$ ；

(3)、由上题的规律计算300＋302＋304＋…＋2016＋2018的值（要有计算过程）。

查看试题解析
17. 为保障校园体育活动安全有序的开展，学校计划在足球场四周安装防护栏．如图，每根立柱的直径为0.08米，相邻两根立柱之间设置一张防护网，每张防护网长3米．

(1)、根据上述信息，完成下表：
立柱根数
2
3
4
5
…
n
防护栏长度（米）
3.16
6.24

12.4
…

(2)、当防护栏总长度为74米时，求立柱的根数，

查看试题解析
18. 如图

(1)、由图1得：2+4＝2×3；由图2得：2+4+6＝；由图3得：；

(2)、则由图n可得：2+4+……+2（n+1）＝；

(3)、根据（2）的结论，求2+4+6+……+1000的值．

查看试题解析

加数的个数n	连续偶数的和S
1	$2 = 1 \times 2$
2	$2 + 4 = 6 = 2 \times 3$
3	$2 + 4 + 6 = 12 = 3 \times 4$
4	$2 + 4 + 6 + 8 = 20 = 4 \times 5$
5	$2 + 4 + 6 + 8 + 10 = 30 = 5 \times 6$

立柱根数	2	3	4	5	…	n
防护栏长度（米）	3.16	6.24		12.4	…

【基础版】新北师大版(2024)数学七上 3.3探索与表达规律 同步练习

一、选择题

二、填空题

三、解答题

【基础版】新北师大版(2024)数学七上 3.3探索与表达规律同步练习