广东省深圳市罗湖区2023-2024学年八年级下学期期末数学试题
试卷更新日期:2024-07-12 类型:期末考试
一、选择题(本题共10小题,每小题3分,共30分,每小题给出4个选项,其中只有一个是正确的)
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、3. 下列从左到右的变形中,是因式分解的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上用阴影表示正确的是( )A、
2. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、3. 下列从左到右的变形中,是因式分解的是( )A、 B、 C、 D、4. 不等式组的解集在数轴上用阴影表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 一个多边形的内角和是外角和的2倍,这个多边形是( )
5. 一个多边形的内角和是外角和的2倍,这个多边形是( )
A、四边形 B、五边形 C、六边形 D、八边形6. 若要分式有意义,则x的值应满足( )A、 B、 C、且 D、x的值为一切实数7. 在图形的平移和旋转变换中,下列说法正确的是( )A、对应点所连线段都平行 B、对应线段都平行 C、对应点所连线段都相等 D、对应线段都相等8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )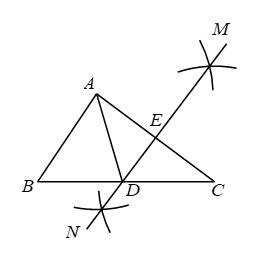 A、13 B、14 C、15 D、169. 如图, 四边形是平行四边形,平分 , 交边于点E,平分交边于点F,P是延长线上一点,则下列结论错误的是( )
A、13 B、14 C、15 D、169. 如图, 四边形是平行四边形,平分 , 交边于点E,平分交边于点F,P是延长线上一点,则下列结论错误的是( ) A、 B、 C、 D、10. 一次函数是常数)与是常数) 的图象交于点 , 下列结论正确的序号是( )
A、 B、 C、 D、10. 一次函数是常数)与是常数) 的图象交于点 , 下列结论正确的序号是( )①关于x的方程的解为;②;③当时,;④若 , 则
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题(本题共5小题,每小题3分,共15分)
-
11. 分解因式: -9= .12. 如图, 小明要测量池塘的宽度 , 选取点O,使D,E分别是 , 中点,现测得的长为28米,则池塘的宽大约是米.
 13. 如图,有一艘轮船位于灯塔的南偏东方向,距离灯塔海里的处,它沿正北方向航行到达位于灯塔正东方向上的处,那么此时轮船与灯塔的距离为海里(结果用含根号的式子表示).
13. 如图,有一艘轮船位于灯塔的南偏东方向,距离灯塔海里的处,它沿正北方向航行到达位于灯塔正东方向上的处,那么此时轮船与灯塔的距离为海里(结果用含根号的式子表示). 14. 如图,在中, , 以点C为圆心,以长为半径作圆弧,交的延长线于点D, 连接 . 若 , 则 .
14. 如图,在中, , 以点C为圆心,以长为半径作圆弧,交的延长线于点D, 连接 . 若 , 则 . 15. 如图中, , , , 将边绕点 B顺时针旋转90°至 , 连 , 则 .
15. 如图中, , , , 将边绕点 B顺时针旋转90°至 , 连 , 则 .
三、解答题(本题共7小题, 共55分,16题8分, 17题5分, 18, 19, 20, 21题各8分,22题10分)
-
16. 解方程和不等式组:(1)、解方程: ;(2)、解不等式组: 并把解集在数轴上表示出来.
 17. 先化简,再求值: , 其中 .18. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点均在格点上,建立平面直角坐标系后,三个顶点的坐标分别为 .
17. 先化简,再求值: , 其中 .18. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点均在格点上,建立平面直角坐标系后,三个顶点的坐标分别为 . (1)、将沿x轴正方向平移8个长度单位得(点 A的对应点为,点 B 的对应点为 , 点C的对应点为画出(2)、作关于原点中心对称的(点A的对应点为 , 点B的对应点为点 C的对应点为 );(3)、四边形的形状 (填“是”或“不是”)平行四边形;(4)、的面积= .19. 如图, 在四边形中, 对角线与相交于点 O,垂足分别为E,F, .
(1)、将沿x轴正方向平移8个长度单位得(点 A的对应点为,点 B 的对应点为 , 点C的对应点为画出(2)、作关于原点中心对称的(点A的对应点为 , 点B的对应点为点 C的对应点为 );(3)、四边形的形状 (填“是”或“不是”)平行四边形;(4)、的面积= .19. 如图, 在四边形中, 对角线与相交于点 O,垂足分别为E,F, . (1)、求证: 四边形是平行四边形.(2)、若 , , , 求的长.20. 李大爷在龙岭街有若干间房屋出租,每间房的租金相同,2022年共收租金万元,2023年因房屋租售行情不好,每间房租金比2022年降低了1000元,2023 年共收租金万元.(1)、李大爷一共有几间房屋出租?(2)、2024年李大爷再次降低房屋租金,但希望年租金不少于万元,则每间房再次降低房屋租金最多可降多少元?21. 本学期,我们学习了“一元一次不等式与一次函数”,请利用所学知识来解决下面的问题:
(1)、求证: 四边形是平行四边形.(2)、若 , , , 求的长.20. 李大爷在龙岭街有若干间房屋出租,每间房的租金相同,2022年共收租金万元,2023年因房屋租售行情不好,每间房租金比2022年降低了1000元,2023 年共收租金万元.(1)、李大爷一共有几间房屋出租?(2)、2024年李大爷再次降低房屋租金,但希望年租金不少于万元,则每间房再次降低房屋租金最多可降多少元?21. 本学期,我们学习了“一元一次不等式与一次函数”,请利用所学知识来解决下面的问题:在函数中, 下表是y与x的几组对应值.
x
…
0
1
2
3
y
...
7
m
3
1
n
1
3
(1)、m= , n= ;(2)、在下面给出的平面直角坐标系中,画出这个函数的图象; (3)、根据图象,下列关于该函数性质的说法中正确的是 . (填序号)
(3)、根据图象,下列关于该函数性质的说法中正确的是 . (填序号)①该函数图象是轴对称图形,对称轴为直线 .
②当时, y随x的增大而增大,当时,y随x的增大而减小.
③该函数在自变量的取值范围内有最小值,当时有最小值 .
(4)、根据图象, 直接写出不等式:的解集 .22.
(1)、【知识再现】如图1, 已知等腰中, , 平分 , D点在上.则与的位置关系是 , , 当 , 时, .(2)、【知识应用】如图2, 在中, , 平分交于E, , 且求的周长.(3)、【知识拓展】如图3,中, , , 是的角平分线,求的值.