广西名校联合2023-2024学年高二下学期期末联考数学试题

试卷更新日期：2024-07-12 类型：期末考试

进入出卷网下载

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 已知函数 $f (x)$ 在 $x = x_{0}$ 处的导数为3，则 $\lim_{Δ x \to 0} \frac{f (x_{0} + Δ x) - f (x_{0})}{2 Δ x} =$ （）

A、3 B、 $\frac{3}{2}$ C、6 D、 $\frac{2}{3}$

查看试题解析
2. 为了促进边疆少数民族地区教育事业的发展，我市教育系统选派了 $3$ 名男教师和 $2$ 名女教师去支援新疆教育，要求这 $5$ 名教师被分派到 $3$ 个学校对口支教，每名教师只去一个学校，每个学校至少安排 $1$ 名教师，其中 $2$ 名女教师分派到同一个学校，则不同的分派方法有( )

A、 $18$ 种 B、 $36$ 种 C、 $68$ 种 D、 $84$ 种

查看试题解析
3. 已知函数 $f (x) = x^{3} - 2 x^{2} + x - 1$ ，则下列说法正确的是( )

A、 $f (x)$ 的极小值为 $- 2$ B、 $f (x)$ 的极大值为 $- \frac{23}{27}$ C、 $f (x)$ 在区间 $(\frac{1}{3}, 1)$ 上单调递增 D、 $f (x)$ 在区间 $(- \infty, 0)$ 上单调递减

查看试题解析
4. 在 $(x - 1) (x - y)^{6}$ 的展开式中，含 $x^{4} y^{3}$ 项的系数为( )

A、 $- 20$ B、 $20$ C、 $- 15$ D、 $15$

查看试题解析
5. 若曲线 $y = (1 - x) e^{x}$ 有两条过点 $A (a, 0)$ 的切线，则 $a$ 的取值范围是（）

A、 $(- \infty, - 1) ∪ (3, + \infty)$ B、 $(- 3, 1)$ C、 $(- \infty, - 3)$ D、 $(- \infty, - 3) ∪ (1, + \infty)$

查看试题解析
6. 已知函数 $f (x) = x^{3} + a x^{2} + b x + a^{2}$ 在 $x = - 1$ 处有极值 $8$ ，则 $f (1)$ 等于( )

A、 $- 4$ B、 $16$ C、 $- 4$ 或 $16$ D、 $16$ 或 $18$

查看试题解析
7. 已知函数 $f (x) = 2 s i n x - e^{x} + e^{- x}$ ，则关于 $x$
不等式 $f (x^{2} - 4) + f (3 x) < 0$ 的解集为( )

A、 $(- 4,1)$ B、 $(- 1,4)$ C、 $(- \infty, - 4) \cup (1, + \infty)$ D、 $[- 1,4]$

查看试题解析
8. 已知 $a = \frac{e^{2}}{l n 3}$ ， $b = e^{e - 1}$ ， $c = \frac{e^{3}}{2 l n 2}$ ，则有( )

A、 $a < b < c$ B、 $a < c < b$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析

二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。

9. 下列求函数的导数正确的是( )

A、 $[l n (2 x + 1)]^{'} = \frac{1}{2 x + 1}$ B、 ${(x^{3} - 2^{x} + 1)}^{^{'}} = 3 x^{2} - 2^{x} l n 2$ C、 $(x s i n x)^{'} = s i n x + x c o s x$ D、 ${(\frac{l n x}{x})}^{^{'}} = \frac{1 - l n x}{x}$

查看试题解析
10. 已知 ${(2 x + \frac{1}{\sqrt[3]{x}})}^{n}$ 的展开式共有 $13$ 项，则下列说法中正确的有( )

A、所有奇数项的二项式系数和为 $2^{11}$ B、所有项的系数和为 $3^{13}$ C、二项式系数最大的项为第 $7$ 项 D、有理项共 $4$ 项

查看试题解析
11. 身高各不相同的六位同学 $A 、 B 、 C 、 D 、 E 、 F$ 站成一排照相，则说法正确的是（）

A、A、C、D三位同学从左到右按照由高到矮的顺序站，共有120种站法 B、A与 $C$ 同学不相邻，共有 $A_{4}^{4} \cdot A_{5}^{2}$ 种站法 C、A、C、D三位同学必须站在一起，且A只能在C与D的中间，共有144种站法 D、A不在排头，B不在排尾，共有504种站法

查看试题解析
12. 已知函数 $f (x) = - x^{3} + 3 x + 2$ ，则（）

A、 $f (x)$ 有两个极值点 $(- 1, 0), (1, 4)$ B、 $f (x)$ 有两个零点 C、直线 $y = 4 x$ 是 $f (x)$ 的切线 D、点 $(0, 2)$ 是 $f (x)$ 的对称中心

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分。

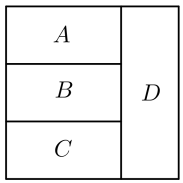
13. ${(2 x - 1)}^{5}$ 的展开式中 $x^{3}$ 的系数为 $($ 用数字作答 $)$ ．

查看试题解析
14. 如图，用4种不同的颜色对图中4个区域涂色，要求每个区域涂1种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有种．

查看试题解析
15. 若函数 $f (x) = a x^{3} + 3 x^{2} - x$ 恰好有三个单调区间，则实数 $a$ 的取值范围是．

查看试题解析
16. 已知函数 $f (x) = \{\begin{array}{l} - x^{3} + x^{2}, x \leq 0 \\ \frac{l n x}{x}, x > 0 \end{array}$ ，若函数 $g (x) = f (x) - m$ 恰有一个实根，则实数 $m$ 的取值范围是

查看试题解析

四、解答题：本题共6小题，共72分。解答应写出文字说明，证明过程或演算步骤。

17. s已知函数 $f (x) = 2 x^{3} - 3 x^{2} - 12 x + 9$ ．

(1)、求曲线 $y = f (x)$ 在 $(1, f (1))$ 处的切线方程；

(2)、求 $f (x)$ 在 $[- 3,3]$ 上的最值．

查看试题解析
18. 若 ${(2 x - a)}^{7} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5} + a_{6} x^{6} + a_{7} x^{7}$ ，且 $a_{4} = - 560$ ．

(1)、求实数 $a$ 的值；

(2)、求 $a_{1} + \frac{a_{2}}{2} + \frac{a_{3}}{2^{2}} + \frac{a_{4}}{2^{3}} + \frac{a_{5}}{2^{4}} + \frac{a_{6}}{2^{5}} + \frac{a_{7}}{2^{6}}$ 的值．

查看试题解析
19. 若 ${(x \sqrt{x} + \frac{1}{x^{4}})}^{n}$ 的展开式中，第二 $､$ 三 $､$ 四项的二项式系数成等差数列．

(1)、求 $n$ 的值；

(2)、此展开式中是否有常数项？若存在，请求出该项；若不存在，请说明理由．

查看试题解析
20. 已知 $0$ ， $1$ ， $2$ ， $3$ ， $4$ ， $5$ ， $6$ 共 $7$ 个数字．

(1)、可以组成多少个没有重复数字的四位数？

(2)、可以组成多少个没有重复数字的四位偶数？

(3)、可以组成多少个没有重复数字且能被 $5$ 整除的四位数？ $($ 结果用数字作答 $)$

查看试题解析
21. 已知函数 $f (x) = a x - l n x - 1 (a \in R)$

(1)、讨论 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 有一个零点，求 $a$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = (a - 1) l n x - \frac{1}{2} x^{2} + x$ ， $a \in R$ ．

(1)、若曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线与直线 $y = 2 x$ 平行，证明： $f (x) \leq l n 4$ ；

(2)、设 $g (x) = \frac{2 x - a}{x} - \frac{1}{2} x^{2}$ ，若对 $\forall x \in (1, + \infty)$ ，均有 $f (x) + 4 > g (x)$ ，求实数 $a$ 的取值范围．

查看试题解析