【提升版】北师大版数学八上2.1认识无理数同步练习

试卷更新日期：2024-07-12 类型：同步测试

进入出卷网下载

一、选择题

1. 在给出的一组数0，π， $\sqrt{5}$ ， 3.14， $\sqrt[3]{9}$ ， $\frac{22}{7}$ 中，无理数有（　　）

A、1个 B、2个 C、3个 D、5个

查看试题解析
2. 在实数-3， $\sqrt{8}$ ， $^{3} \sqrt{- 8}$ 2-8，-0.518， $\frac{π}{2}$ ， 0.101001……中，无理数的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列说法正确的有（）
①无限小数不一定是无理数；②无理数一定是无限小数；③带根号的数不一定是无理数；④不带根号的数一定是有理数．

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
4. 下列说法中，正确的个数为（）
①无限小数都是无理数：

②无限不循环小数都是无理数；

③无理数都是无限小数：

④无理数也有负数；

⑤无理数分为正无理数、零、负无理数.

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 在 $\sqrt{5}$ ， $- \frac{1}{3}$ ， $0.6$ ， -1， $2 π$ ， $\sqrt{4}$ ， $7.0101001 \dots$ （每两个“1”之间依次多一个“0”），这7个数中，无理数共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 在实数﹣2， $\sqrt{7}$ ， 3.1415926， $\frac{1}{7} ， \sqrt{0.25}$ ， ﹣π＋1，0.1010010010001中，无理数有（）个

A、2 B、3 C、4 D、5

查看试题解析
7. 如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（　　）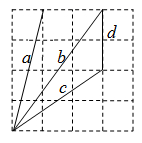

A、1 条 B、2条 C、3条 D、4条

查看试题解析
8. 如图为5×5的正方形格子，其中所有线段的端点都在格点上，长度是无理数的线段有（）

A、b、c、d B、c、d C、a、d D、b、c

查看试题解析

二、填空题

9. 在实数： $3.14159$ ， $\sqrt[3]{64}$ ， $1.010010001 \dots$ ， $4$ ． $\overset{\cdot}{2} \overset{\cdot}{1}$ ， $π$ ， $\sqrt{3}$ ， $\frac{22}{7}$ 中，无理数有．

查看试题解析
10. 若 $a$ 、 $b$ 都是无理数，且 $a + b = 2$ ，则 $a$ 、 $b$ 的值可以是（填上一组满足条件的值即可）.

查看试题解析
11. 下列各数：①-0.3，②0，③ $\sqrt{5}$ ，④π² ， ⑤|-2|，⑥ $\sqrt[3]{8}$ ，⑦3.1010010001…（每两个1之间多一个0），⑧- $\frac{22}{7}$ 中无理数有（只填序号）.

查看试题解析
12. 如图，在5×5的正方形网格中，以AB为边画直角△ABC，使点C在格点上，且另外两条边长均为无理数，满足这样条件的点C共个．

查看试题解析

三、解答题

13. 如图，每个小正方形的边长都是1．按要求画图（所画图形的顶点都是格点，标字母，写结论）
①面积为13的正方形（边长是无理数）；
②三条边长都是无理数的直角三角形．

查看试题解析
14. 定义：可以表示为两个互质整数的商的形式的数称为有理数，整数可以看作分母为1的有理数；反之为无理数．如 $\sqrt{2}$ 不能表示为两个互质的整数的商，所以， $\sqrt{2}$ 是无理数．
可以这样证明：
设 $\sqrt{2} = \frac{a}{b}$ ,a与b 是互质的两个整数，且b≠0．
则 $2 = \frac{a^{2}}{b^{2}}$ a²=2b²因为b是整数且不为0，所以，a是不为0的偶数，设a=2n，（n是整数），所以b²=2n² ，所以b也是偶数，与a，b是互质的正整数矛盾．所以， $\sqrt{2}$ 是无理数．仔细阅读上文，然后，请证明： $\sqrt{5}$ 是无理数．

查看试题解析

【提升版】北师大版数学八上2.1认识无理数 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学八上2.1认识无理数同步练习