【提升版】北师大版数学九上2.2用配方法解一元二次方程同步练习

试卷更新日期：2024-07-11 类型：同步测试

进入出卷网下载

一、选择题

1. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，配方结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
2. 用配方法解下列方程时，配方错误的是（）

A、 $x^{2} + 2 x - 99 = 0$ 化为 ${(x + 1)}^{2} = 100$ B、 $2 x^{2} - 7 x - 4 = 0$ 化为 ${(x - \frac{7}{4})}^{2} = \frac{81}{16}$ C、 $x^{2} + 8 x + 9 = 0$ 化为 ${(x + 4)}^{2} = 25$ D、 $3 x^{2} - 4 x - 2 = 0$ 化为 ${(x - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
3. 若关于 $x$ 的一元二次方程 $x^{2} - 8 x + c = 0$ 配方后得到方程 $(x - 4)^{2} = 3 c$ ，则 $c$ 的值为（）

A、 $- 4$ B、 $0$ C、 $4$ D、 $6$

查看试题解析
4. 如图是嘉淇用配方法解一元二次方程的具体过程，老师说这个解法出现了错误，则开始出现错误的步骤是（）

A、② B、③ C、④ D、⑤

查看试题解析
5. 用配方法解方程 $4 x^{2} - 2 x - 1 = 0$ 时，配方结果正确的是（）．

A、 ${(x - \frac{1}{2})}^{2} = \frac{1}{2}$ B、 ${(x - \frac{1}{4})}^{2} = \frac{1}{2}$ C、 ${(x - \frac{1}{4})}^{2} = \frac{3}{16}$ D、 ${(x - \frac{1}{4})}^{2} = \frac{5}{16}$

查看试题解析
6. 用配方法解方程 $3 x^{2} + 8 x - 3 = 0$ ，则方程可变形为（）

A、 ${(x + \frac{4}{3})}^{2} = 1$ B、 ${(x + \frac{4}{3})}^{2} = \frac{43}{9}$ C、 ${(x + \frac{4}{3})}^{2} = \frac{25}{9}$ D、 ${(x - \frac{4}{3})}^{2} = \frac{25}{9}$

查看试题解析
7. 用配方法解一元二次方程ax²+bx+c=0（a≠0），此方程可变形为（）

A、（x+ $\frac{b}{2 a}$ ）²= $\frac{b^{2} - 4 a c}{4 a^{2}}$ B、（x+ $\frac{b}{2 a}$ ）²= $\frac{4 a c - b^{2}}{4 a^{2}}$ C、（x﹣ $\frac{b}{2 a}$ ）²= $\frac{b^{2} - 4 a c}{4 a^{2}}$ D、（x﹣ $\frac{b}{2 a}$ ）²= $\frac{4 a c - b^{2}}{4 a^{2}}$

查看试题解析
8. 老师设计了接力游戏，用合作的方式完成配方法解方程，规则：每人只能看到前一人给的方程，并进行一步计算，再将结果传递给下一人，最后解出方程，过程如图所示，接力中，自己负责的一步出现错误的是（）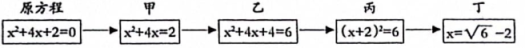

A、只有甲 B、只有丁 C、乙和丁 D、甲和丁

查看试题解析

二、填空题

9. 下面是用配方法解关于x的一元二次方程 $3 x^{2} + x - 2 = 0$ 的具体过程，
$3 x^{2} + 2 x - 1 = 0$
解：第一步： $x^{2} + \frac{2}{3} x - \frac{1}{3} = 0$
第二步： $x^{2} + \frac{2}{3} x = \frac{1}{3}$
第三步： $x^{2} + \frac{2}{3} x + {(\frac{1}{3})}^{2} = \frac{1}{3} + {(\frac{1}{3})}^{2}$
第四步： ${(x + \frac{1}{3})}^{2} = \frac{4}{9}$ $∴ x + \frac{1}{3} = \pm \frac{2}{3}$ $∴ x_{1} = \frac{1}{3}$ ， $x_{2} = - 1$
以下四条语句与上面四步对应：“①移项：方程左边为二次项和一次项，右边为常数项；②求解：用直接开方法解一元二次方程；③配方：根据完全平方公式，在方程的两边各加上一次项系数一半的平方；④二次项系数化1，方程两边都除以二次项系数”，则第一步，第二步，第三步，第四步应对应的语句分别是．

查看试题解析
10. 若将方程 $x^{2} + 8 x = 7$ 化为 ${(x + m)}^{2} = 23$ ，则 $m =$ ．

查看试题解析
11. 若方程x²－4084441＝0的两根为±2021，则方程x²－2x－4084440＝0的两根为．

查看试题解析
12. 将方程 $x^{2} - 6 x + 1 = 0$ 化成 ${(x + a)}^{2} = b$ 的形式，则a+b= ．

查看试题解析
13. 已知x，y，z为实数，且2x﹣3y+z=3，则x²+（y﹣1）²+z²的最小值为．

查看试题解析

三、解答题

14.

(1)、解方程： $x^{2} - 4 x - 1 = 0$ ；

(2)、先化简，再求值： $\frac{x^{2} - 2 x}{x^{2} - 1} \div (x - 1 - \frac{2 x - 1}{x + 1})$ ，其中x是方程 $y^{2} - 4 y - 5 = 0$ 的解．

查看试题解析
15. 嘉琪准备完成题目：解一元二次方程 $x^{2} - 6 x + = 0$ ．

(1)、若“ ”表示常数 $- 7$ ，请你用配方法解方程： $x^{2} - 6 x - 7 = 0$ ；

(2)、若“ ”表示一个字母，且一元二次方程 $x^{2} - 6 x + = 0$ 有实数根．求“ ”的最大值．

查看试题解析
16. 先化简，再求值： $(\frac{x}{x - 1} - \frac{x + 1}{x})$ ÷ $\frac{x^{2} + 4 x + 4}{x^{2} - x}$ ，其中x是方程x²+4x+1＝0的根．

查看试题解析
17.

(1)、解方程： $3 （ x - 2 ）^{2} = 2 - x$ ．

(2)、下面是小明解一元二次方程的过程，请认真阅读并完成相应的任务．
解： $2 x^{2} + 4 x - 8 = 0$
二次系数化为 $1$ ，得 $x^{2} + 2 x - 4 = 0 \dots$ 第一步
移项，得 $x^{2} + 2 x = 4 \dots$ 第二步
配方，得 $x^{2} + 2 x + 4 = 4 + 4$ ，即 $（ x + 2 ）^{2} = 8 \dots$ 第三步
由此，可得 $x + 2 = \pm 2 \sqrt{2} \dots$ 第四步
所以， $x_{1} = 2 + 2 \sqrt{2}$ ， $x_{2} = - 2 - 2 \sqrt{2} \dots$ 第五步
任务：
$①$ 上面小明同学的解法中运用“配方法”将该一元二次方程“降次”为两个一元一次方程，体现的数学思想是    ▲         ，其中“配方法”所依据的一个数学公式是    ▲        ；
$②$ “第二步”变形的依据是    ▲        ；
$③$ 上面小明同学解题过程中，从第    ▲        步开始出现错误，请直接写出正确的解是    ▲        ；
$④$ 请你根据平时学习经验，就解一元二次方程时还需要注意的事项为其他同学提一条意见．

查看试题解析
18. 下面是小聪同学用配方法解方程： $2 x^{2} - 4 x - p = 0$ $(p > 0)$ 的过程，请仔细阅读后，解答下面的问题．
$2 x^{2} - 4 x - p = 0$
解：移项，得： $2 x^{2} - 4 x = p$ ． ①
二次项系数化为1，得： $x^{2} - 2 x = \frac{p}{2}$ ． ②
配方，得 $x^{2} - 2 x + 1 = \frac{p}{2}$ ． ③
即 $(x - 1)^{2} = \frac{p}{2}$ .
∵ $p > 0$ ，
∴ $x - 1 = \pm \sqrt{\frac{p}{2}}$ ． ④
∴ $x_{1} = 1 + \frac{\sqrt{2 p}}{2}$ ， $x_{1} = 1 - \frac{\sqrt{2 p}}{2}$ ． ⑤

(1)、第②步二次项系数化为1的依据是什么？

(2)、整个解答过程是否正确？若不正确，说出从第几步开始出现的错误，并直接写出此方程的解．

查看试题解析

【提升版】北师大版数学九上2.2用配方法解一元二次方程 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学九上2.2用配方法解一元二次方程同步练习