【提升版】北师大版数学八上第一章 勾股定理 单元测试卷
试卷更新日期:2024-07-10 类型:单元试卷
一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的)
-
1. 下列几组数中,不能作为直角三角形三边的是( )A、1, , B、7,24,25 C、4,5,6 D、 , ,12. 以直角三角形的三边为边做正方形,三个正方形的面积如图,正方形A的面积为( )
 A、6 B、36 C、64 D、83. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
A、6 B、36 C、64 D、83. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )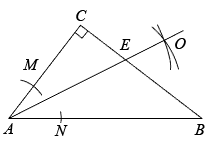 A、8 B、7 C、6 D、54. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( )
A、8 B、7 C、6 D、54. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( ) A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则CE的长是( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和5. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则CE的长是( ) A、 B、 C、 D、6. 明朝数学家程大位在数学著作《直指算法统宗》中,以《西江月》词牌叙述了一道“荡秋千”问题:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地.意思是:如图,秋千OA静止的时候,踏板离地高一尺(尺),将它往前推进两步,一步合5尺(尺),此时踏板离地五尺(尺),则秋千绳索的长度为( )
A、 B、 C、 D、6. 明朝数学家程大位在数学著作《直指算法统宗》中,以《西江月》词牌叙述了一道“荡秋千”问题:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地.意思是:如图,秋千OA静止的时候,踏板离地高一尺(尺),将它往前推进两步,一步合5尺(尺),此时踏板离地五尺(尺),则秋千绳索的长度为( )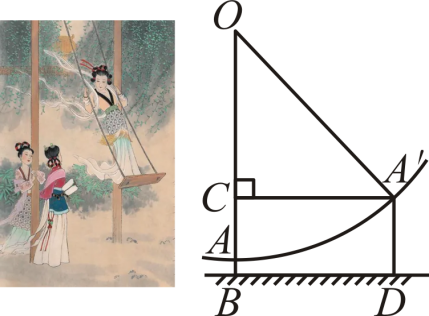 A、尺 B、尺 C、20尺 D、29尺7. 如图,在中,平分交于点 , 则点到的距离是( )
A、尺 B、尺 C、20尺 D、29尺7. 如图,在中,平分交于点 , 则点到的距离是( )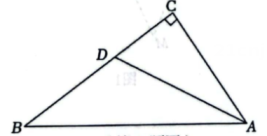 A、3 B、4 C、5 D、68. 如图1,2002年8月在北京召开的国际数学家大会会标原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成.如图2,如果大正方形的面积是16,直角三角形的直角边长分别为 , , 且 , 那么图中小正方形的面积是( )
A、3 B、4 C、5 D、68. 如图1,2002年8月在北京召开的国际数学家大会会标原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成.如图2,如果大正方形的面积是16,直角三角形的直角边长分别为 , , 且 , 那么图中小正方形的面积是( )图1
 图2
图2 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本大题共5小题, 每小题3分, 共15分)
-
9. 如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为.
 10. 如图,长方形 ABCD 中,点 E 在边 AB 上,将一边 AD 折叠,使点 A恰好落在边 BC 的点 F 处,折痕为 DE.若 AB=4,BF=2,则 AE的长是 .
10. 如图,长方形 ABCD 中,点 E 在边 AB 上,将一边 AD 折叠,使点 A恰好落在边 BC 的点 F 处,折痕为 DE.若 AB=4,BF=2,则 AE的长是 .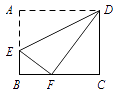 11. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .12. 如图是一个三级台阶,它的每一级的长、宽、高分别为 , 和 , 和 是这个台阶的两个端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为 .
11. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为 .12. 如图是一个三级台阶,它的每一级的长、宽、高分别为 , 和 , 和 是这个台阶的两个端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为 . 13. 如图,在中, , 于点 , , , 则 .
13. 如图,在中, , 于点 , , , 则 .
三、解答题 (共7题;共61分)
-
14. 如图,在的网格中,每个小正方形的边长均为一个单位长度,的三个顶点都在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
 (1)、;(2)、在图1中确定一点D , 点D在边上,使;(3)、在图2中确定一点E , 点E在边上,使平分 .15. 如图,中, , , 是边上一点,且 , 若求的长.
(1)、;(2)、在图1中确定一点D , 点D在边上,使;(3)、在图2中确定一点E , 点E在边上,使平分 .15. 如图,中, , , 是边上一点,且 , 若求的长. 16. 如图,在中, , , , D为AB中点,点E , F分别在直线BC , AC上, , 连接EF .
16. 如图,在中, , , , D为AB中点,点E , F分别在直线BC , AC上, , 连接EF . (1)、当点E与点B重合时,求EF的长;(2)、当点F不与点A重合时,求证:;(3)、若 , 求线段CF的长.17. 在△ABC中,∠C= 90°,AC=6,BC=8,D,E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,顶点B的对应点是B'.
(1)、当点E与点B重合时,求EF的长;(2)、当点F不与点A重合时,求证:;(3)、若 , 求线段CF的长.17. 在△ABC中,∠C= 90°,AC=6,BC=8,D,E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,顶点B的对应点是B'. (1)、如图1,如果点B'和顶点A重合,求CE的长.(2)、如图2,如果点B'落在AC的中点上,求CE的长.18. 拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
(1)、如图1,如果点B'和顶点A重合,求CE的长.(2)、如图2,如果点B'落在AC的中点上,求CE的长.18. 拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变). 19. 已知:如图,有一块的绿地,量得两直角边m, , 现要将这块绿地扩充成等腰 , 且扩充部分()是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长.
19. 已知:如图,有一块的绿地,量得两直角边m, , 现要将这块绿地扩充成等腰 , 且扩充部分()是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长. (1)、在图1中,当m时,的周长为;(2)、在图2中,当m时,的周长为;(3)、在图3中,当时,求的周长.20. 某数学活动小组在一次活动中,对一个数学问题做如下研究:
(1)、在图1中,当m时,的周长为;(2)、在图2中,当m时,的周长为;(3)、在图3中,当时,求的周长.20. 某数学活动小组在一次活动中,对一个数学问题做如下研究: (1)、如图1,在△ABC中分别以AB,AC为边向外作等腰三角形ABE和等腰三角形ACD,使连结BD,CE,则BD与CE的大小关系为.(2)、如图2,在△ABC中分别以AB,AC为边向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠CAD=90°,连结BD,CE,若AB=4,BC=2,∠ABC=45°,求BD的长.
(1)、如图1,在△ABC中分别以AB,AC为边向外作等腰三角形ABE和等腰三角形ACD,使连结BD,CE,则BD与CE的大小关系为.(2)、如图2,在△ABC中分别以AB,AC为边向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠CAD=90°,连结BD,CE,若AB=4,BC=2,∠ABC=45°,求BD的长.