【基础版】北师大版数学八上第一章 勾股定理 单元测试卷
试卷更新日期:2024-07-10 类型:单元试卷
一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的)
-
1. 已知△ABC中,a、b、c分别是∠A,∠B,∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )A、∠A=∠C-∠B B、a2=b2-c2 C、a:b:c=2:3:4 D、a= ,b= ,c=12. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、133. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时, 梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5m,则小巷的宽为( ).
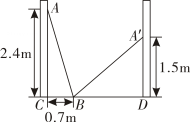 A、2.4m B、2m C、2.5m D、2.7m4. 如图,△ABC中,D为AC的中点,CE⊥AB于点E , 若DE=3,AE=5,则CE=( )
A、2.4m B、2m C、2.5m D、2.7m4. 如图,△ABC中,D为AC的中点,CE⊥AB于点E , 若DE=3,AE=5,则CE=( )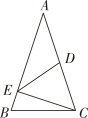 A、3 B、4 C、 D、5. 在中, , , , 则斜边上的高等于( )A、5 B、 C、12 D、6. 如图,以一直角三角形的三边分别向外作正方形,其中两个正方形的面积如图所示,则B所代表的正方形的面积为( )
A、3 B、4 C、 D、5. 在中, , , , 则斜边上的高等于( )A、5 B、 C、12 D、6. 如图,以一直角三角形的三边分别向外作正方形,其中两个正方形的面积如图所示,则B所代表的正方形的面积为( ) A、144 B、196 C、256 D、3047. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )
A、144 B、196 C、256 D、3047. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )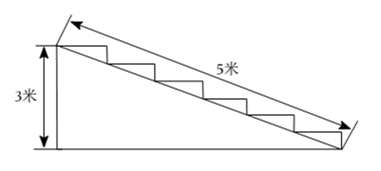 A、米 B、米 C、米 D、米8. 如图, , 则数轴上点A所表示的数为( )
A、米 B、米 C、米 D、米8. 如图, , 则数轴上点A所表示的数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题, 每小题3分, 共15分)
-
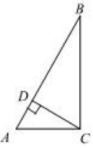
9. 在三角形ABC中,∠C=90°,AB=7,BC=5,则AC的长为.10. 如图,在中,于点 , 且 , 那么 .
 11. 如图,是一个三级台阶,它的每一级的长、宽,高分别为 , 、 , 和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程是。
11. 如图,是一个三级台阶,它的每一级的长、宽,高分别为 , 、 , 和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程是。 12. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .
12. 如图,在△ABC中,已知∠A为钝角,边AB,AC的中垂线分别交BC于点D,E.若BD2+CE2=DE2 , 则∠A= .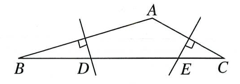 13. 如图,一个圆桶,底面直径为 , 高为 , 则一只小虫从下底部点爬到上底点处,问小虫所爬的最短路径长是取 .
13. 如图,一个圆桶,底面直径为 , 高为 , 则一只小虫从下底部点爬到上底点处,问小虫所爬的最短路径长是取 .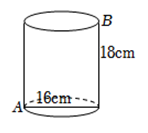
三、解答题 (共7题;共61分)
-
14. 若△ABC中,∠C=90°.(1)、若 , 求;(2)、若求;15. 作图题:如图,在5×5的正方形网格中,每个小正方形的边长均为1,A , B两点都在格点上,连结AB , 请完成下列作图.请按要求画出格点三角形.

⑴在图1中找一个格点C , 使得是等腰三角形(作一个即可);
⑵在图中2找一个格点D , 使得是直角三角形且其三边都不与网格线重合.(作一个即可).
16. 如图所示,A城与C城的直线距离为60公里,B城与C城的直线距离为80公里,A城与B城的直线距离为100公里. (1)、现需要在A , B , C三座城市所图成的三角形区域内建造一个加油站 . 使得这个加油站到三座城市A , B , C的距离相等,则加油站点一定是三条的交点;(请在以下选项中选出正确答案并将对应选项序号填写在横线上:①中线②高线③角平分线④垂直平分线)(2)、判断形状,并说明理由.17. 如图,一辆小汽车在一段限速高速公路上沿直道行驶,某一时刻刚好行驶到路对面车速检测仪的正前方的处,过了后,测得小汽车到达与车速检测仪之间的距离为的处.
(1)、现需要在A , B , C三座城市所图成的三角形区域内建造一个加油站 . 使得这个加油站到三座城市A , B , C的距离相等,则加油站点一定是三条的交点;(请在以下选项中选出正确答案并将对应选项序号填写在横线上:①中线②高线③角平分线④垂直平分线)(2)、判断形状,并说明理由.17. 如图,一辆小汽车在一段限速高速公路上沿直道行驶,某一时刻刚好行驶到路对面车速检测仪的正前方的处,过了后,测得小汽车到达与车速检测仪之间的距离为的处. (1)、你能计算这辆小汽车的速度吗?(2)、这辆小汽车超速了吗?
(1)、你能计算这辆小汽车的速度吗?(2)、这辆小汽车超速了吗?


