【培优版】北师大版数学八上1.3勾股定理的应用同步练习

试卷更新日期：2024-07-10 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，圆柱底面半径为 $\frac{4}{π} c m$ ，高为 $18 c m$ ，点 $A$ 、 $B$ 分别是圆柱两底面圆周上的点，且 $A$ 、 $B$ 在同一母线上，用一根棉线从 $A$ 点顺着圆柱侧面绕 $3$ 圈到 $B$ 点，则这根棉线的长度最短为（）

A、 $24 c m$ B、 $30 c m$ C、 $2 \sqrt{21} c m$ D、 $4 \sqrt{97} c m$

查看试题解析
2. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用 $x$ 、 $y$ 表示直角三角形的两直角边 $(x > y)$ ，下列四个说法：① $x^{2} + y^{2} = 49$ ，② $x \cdot y = 2$ ，③ $2 x y + 4 = 49$ ，④ $x + y = 9$ ．其中说法正确的是（）

A、①③ B、①②③ C、①②④ D、①②③④

查看试题解析
3. 勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可用其面积关系验证勾股定理.图2是由图1放入矩形内得到的， $∠ B A C = 90 °$ ， $A B = 6$ ， $A C = 8$ .点D，E，F，G，H，I都在矩形 $K L M J$ 的边上，则矩形 $K L M J$ 的面积为（）．

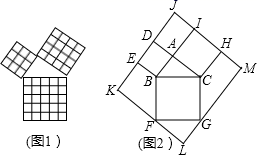A、288 B、400 C、432 D、440

查看试题解析
4. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn，门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺（1尺＝10寸），则AB的长是（　　）

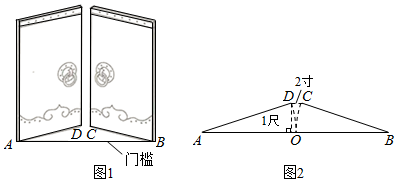A、50.5寸 B、52寸 C、101寸 D、104寸

查看试题解析
5. 如图，在长方体 $A B C D - E F G H$ 盒子中， $A B = 4 c m$ ， $B C = 3 c m$ ， $C G = 5 c m$ ，长为10cm的细直木棒IJ恰好从小孔G处插入，木棒的一端I与底面ABCD接触.当木棒的端点I在长方形ABCD内及边界运动时，GJ长度的最小值为（）

A、 $(10 - 5 \sqrt{2}) c m$ B、3cm C、 $(10 - 4 \sqrt{2}) c m$ D、5cm

查看试题解析
6. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为 $x$ 尺，则可列方程为（）

A、 $x^{2} - 6 = {(10 - x)}^{2}$ B、 $x^{2} - 6^{2} = {(10 - x)}^{2}$ C、 $x^{2} + 6 = {(10 - x)}^{2}$ D、 $x^{2} + 6^{2} = {(10 - x)}^{2}$

查看试题解析
7. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时（即水平距离 $C D = 6 m$ ），踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是（） $m$

A、 $\frac{21}{2}$ B、 $\frac{15}{2}$ C、6 D、 $\frac{9}{2}$

查看试题解析
8. 现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，如图（1）已知云梯最多只能伸长到15m，消防车高3m．救人时云梯伸长至最长，在完成从12m高处救人后，还要从15m高处救人，这时消防车要从原处再向着火的楼房靠近的距离 $A C$ 为（）

A、3米 B、5米 C、7米 D、9米

查看试题解析

二、填空题

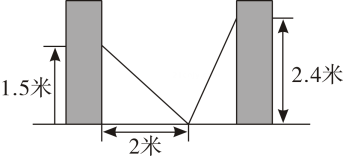
9. 如图，小巷左右两侧是竖直的墙壁，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为2米，顶端距离地面1.5米．若梯子底端位置保持不动，将梯子斜靠在右墙时，顶端距离地面2.4米，则小巷的宽度为米．

查看试题解析
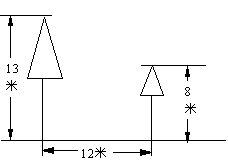
10. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞米.

查看试题解析
11. 某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯．已知楼梯总高度5米，楼梯长13米，主楼道宽2米；这种红色地毯的售价为每平方米30元，其侧面如图所示，则购买地毯至少需要元．

查看试题解析
12. 在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的大意是：如图，有一个水池，水面是一个边长为10尺的正方形．在水池正中央有一根新生的芦苇，它高出水面1尺．如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，则这个水池的深度是尺．

查看试题解析
13. 如图是某路口处草坪的一角，当行走路线是 $A \to C \to B$ 时，有人为了抄近道而避开路的拐角 $∠ A C B$ $(∠ A C B = 90 °)$ ，于是在草坪内走出了一条不该有的捷径路 $A B$ .某学习实践小组通过测量可知， $A C$ 的长约为6米， $B C$ 的长约为8米，为了提醒居民爱护草坪，他们想在A， $B$ 处设立“踏破青白可惜，多行数步无妨”的提示牌．则提示牌上的“多行数步”是指多行米．

查看试题解析

三、解答题

14. 如图，在一条绷紧的绳索一端系着一艘小船．河岸上一男孩拽着绳子另一端向右走，绳端从 $C$ 移动到 $E$ ，同时小船从 $A$ 移动到 $B$ ，且绳长始终保持不变． $A$ 、 $B$ 、 $F$ 三点在一条直线上， $C F ⊥ A F$ ．回答下列问题：

(1)、根据题意可知： $A C$ $B C + C E$ （填“＞”、“＜”、“＝”）．

(2)、若 $C F = 6$ 米， $A F = 8$ 米， $A B = 3$ 米，求小男孩需向右移动的距离（结果保留根号）．

查看试题解析
15. 为了丰富少年儿童的业余生活，某社区要在如图所示的AB所在的直线上建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于点A，DB⊥AB于点B，已知AB＝5千米，CA＝3千米，DB＝2千米，试问：

(1)、图书室E应该建在距点A多少千米处，即AE＝千米，才能使它到两所学校的距离相等？

(2)、证明上题中的结论.

查看试题解析
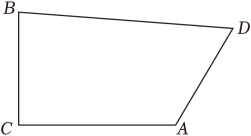
16. 学校正在增加绿化区域，种植花草树木，提高校园的绿化覆盖率，准备在四边形的空地上种植花卉，如图所示， $∠ C = 90 °$ ， $A C = 12 m$ ， $B C = 9 m$ ， $B D = 17 m$ ， $A D = 8 m$ ，求四边形 $A B C D$ 的面积．

查看试题解析
17. 如图，在一条东西走向河流的一侧有一村庄 $C ，$ 河边原有两个取水点 $A ，$ $B ，$ 其中 $A B = A C ，$ 由于某种原因，由 $C$ 到 $A$ 的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点 $H （ A 、 H 、 B$ 在同一条直线上），并新修一条路 $C H ，$ 测得 $C B = 1.5$ 千米， $C H = 1.2$ 千米， $H B = 0.9$ 千米.

(1)、问 $C H$ 是否为从村庄 $C$ 到河边的最近路.请通过计算加以说明；

(2)、求新路 $C H$ 比原路 $C A$ 少多少千米.

查看试题解析
18. 如图，曲柄连杆装置是很多机械上不可缺少的，曲柄 $O A$ （定长）绕固定点 $O$ 做圆周运动，连杆 $A P$ （定长）拉动活塞做往复运动.如图1，当曲柄的 $A$ 端运动到最右边时（ $P ， O ， A$ 三点共线）， $O P$ 的长为 $8 cm$ .如图2，当曲柄的 $A$ 端运动到最左边时（点 $P ， A ， O$ 三点共线）， $O P$ 的长为 $18 cm$ .

(1)、求曲柄 $O A$ 和连杆 $A P$ 的长；

(2)、如图3，当 $O A ⊥ O P$ 时，求 $O P$ 的长.

查看试题解析
19. 如图，小明家在一条东西走向的公路 $M N$ 北侧 $200$ 米的点A处，小红家位于小明家北 $500$ 米（ $A C = 500$ 米）、东 $1200$ 米（ $B C = 1200$ 米）点B处．

(1)、求小明家离小红家的距离 $A B$ ；

(2)、现要在公路 $M N$ 上的点P处建一个快递驿站，使 $P A + P B$ 最小，请确定点P的位置，并求 $P A + P B$ 的最小值．

查看试题解析
20. 阅读材料，回答问题：

(1)、中国古代数学著作图 $1 《$ 周髀算经 $》$ 有着这样的记载：“勾广三，股修四，经隅五．” $.$ 这句话的意思是：“如果直角三角形两直角边为3和4时，那么斜边的长为 $5.$ ” $.$ 上述记载表明了：在 $Rt △ ABC$ 中，如果 $∠ C = 90 °$ ， $BC = a$ ， $AC = b$ ， $AB = c$ ，那么a，b，c三者之间的数量关系是：．

(2)、对于这个数量关系，我国汉代数学家赵爽根据“赵爽弦图” $($ 如图2，它是由八个全等直角三角形围成的一个正方形 $)$ ，利用面积法进行了证明．参考赵爽的思路，将下面的证明过程补充完整：
证明： $∵ S_{△ ABC =} \frac{1}{2} ab$ ， $S_{正方形 ABCD} = c^{2}$ ，

$S_{正方形 MNPQ} =$ ．

又 $∵$ $=$ ，

$∴ {(a + b)}^{2} = 4 \times \frac{1}{2} ab + c^{2}$ ，

整理得 $a^{2} + 2 ab + b^{2} = 2 ab + c^{2}$ ，

$∴$ ．

(3)、如图3，把矩形ABCD折叠，使点C与点A重合，折痕为EF，如果 $AB = 4$ ， $BC = 8$ ，求BE的长．

查看试题解析

【培优版】北师大版数学八上1.3勾股定理的应用 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学八上1.3勾股定理的应用同步练习