【提升版】北师大版数学八上1.3勾股定理的应用 同步练习
试卷更新日期：2024-07-10 类型：同步测试
一、选择题
-
1. 《九章算术》中记录了这样一则“折竹抵地”问题：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远（如图），则折断后的竹子高度为多少尺？（1丈=10尺）如果我们假设折断后的竹子高度为尺，根据题意，可列方程为（ ）
A、 B、 C、 D、2. 小华新买了一条跳绳，如图1，他按照体育老师教的方法确定适合自己的绳长：一脚踩住绳子的中央，手肘靠近身体，两肘弯屈 ， 小臂水平转向两侧，两手将绳拉直，绳长即合适长度。将图1抽象成如图2，若两手握住的绳柄两端距离约为1米，小臂到地面的距离约1. 2米，则适合小华的绳长为（ ）
A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米3. 小强家因装修准备用电梯搬运一些木条上楼，如图，已知电梯的长、宽、高分别是 ， ， ， 那么电梯内能放入下列木条中的最大长度是（ ）
A、 B、 C、 D、4. 如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，若知道图中阴影部分的面积，则一定能求出（ ）
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和5. 白日登山望烽火，黄昏饮马傍交河．诗中隐含着一个有趣的数学问题：诗中将军在观望烽火之后从山脚上的A点出发，奔向小河旁边的P点饮马，饮马后再到B点宿营，若A、B到水平直线l（l表示小河）的距离分别是2，1，AB两点之间水平距离是4，则AP+PB最小值为（ ）
A、3 B、4 C、5 D、66. 如图，是一个外轮廓为长方形的机器零件平面示意图，根据图中标注的尺寸，（单位：），可得两圆孔中心和的距离是（ ）
A、 B、 C、 D、7. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn，门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺（1尺＝10寸），则AB的长是（ ）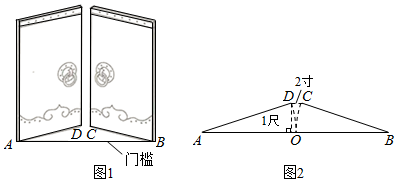
A、50.5寸 B、52寸 C、101寸 D、104寸8. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为时，顶部边缘处离桌面的高度为 ， 此时底部边缘处与处间的距离为 ， 小组成员调整张角的大小继续探究，最后发现当张角为时（是的对应点），顶部边缘处到桌面的距离为 ， 则底部边缘处与之间的距离为（ ）
A、 B、 C、 D、二、填空题
-
9. 如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，在中，若直角边 ， ， 将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是 ．
10. 图1为手机支架实物图，图2为它的侧面示意图，“L型”托架A-C-E用于放置手机，支架BD两端分别与托架和底座MN(其厚度忽略不计)相连，支架B端可调节旋转角度，已知BD=6cm，AB=2BD=4BC，支架调整到图2位置时，∠BDM=60°，∠ABD=120°．因实际需要，现将支架B端角度调整为∠ABD=150°，如图3所示，则点A的位置较原来的位置上升高度为cm．
11. 已知，如图，一轮船从港口A出发向东北方向航行了50海里，另一轮船同时从港口A出发向东南方向航行120海里，此时则两船相距海里 .
12. 在平静的湖面上，有一朵荷花高出水面半尺，忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面．花在水平方向上离开原来的位置2尺远，则这个湖的水深是尺．
13. 如图是一个提供床底收纳支持的气压伸缩杆，除了AB是完全固定的钢架外，AD，BC，DE属于位置可变的定长钢架.如图1所示， ， 伸缩杆PQ的两端分别固定在BC，CE两边上，其中.当伸缩杆PQ打开最大时，如图2所示，成 ， 此时 ， 则可变定长钢架CD的长度为.当伸缩杆完全收拢时， ， 则此时床高(CD与AB之间的距离）为cm.
三、解答题
-
14. 台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向 由 行驶向 ，已知点 为一海港，且点 与直线 上的两点 ， 的距离分别为 ， ，又 ，以台风中心为圆心周围 以内为受影响区域．
(1)、求 的度数．(2)、海港 受台风影响吗？为什么？(3)、若台风的速度为20千米/小时，当台风运动到点 处时，海港 刚好受到影响，当台风运动到点 时，海港 刚好不受影响，即 ，则台风影响该海港持续的时间有多长？15. 八（1）班小明和小亮同学学习了“勾股定理”之后，为了测得下图风筝CE的高度，他们进行了如下操作：①测得BD的长度为24米；
②根据手中剩余线的长度计算出风筝线BC的长为30米；
③牵线放风筝的小明身高AB为1.68米．
(1)、求风筝的高度CE；(2)、若小亮让风筝沿CD方向下降了8米到点M（即CM=8米），则他往回收线多少米？16. 某校八年级（1）班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 ， 他们进行了如下操作：①测得水平距离的长为12米；②根据手中剩余线的长度计算出风筝线的长为20米；③牵线放风筝的小明的身高为1.62米.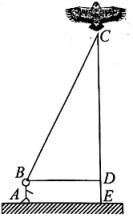
(1)、求风筝的垂直高度；(2)、如果小明想风筝沿方向下降11米，则他应该往回收线多少米？17. 在一条东西走向的河流一侧有一村庄 ， 河边原有两个取水点 ， ， 其中 ， 由于某种原因，由到的路现在已经不通，该村为方便村民取水，决定在河边新建一个取水点、、在同一条直线上 ， 并新修一条路 ， 测得千米，千米，千米．
(1)、求证：；
(2)、求原来的路线的长；18. 如图，某住宅社区在相邻两楼之间修建一个上方是以AB为直径的半圆，下方是长方形的仿古通道，已知AD＝2.3米，CD＝2米；现有一辆卡车装满家具后，高2.5米，宽1.6米，请问这辆送家具的卡车能否通过这个通道？请说出你的理由．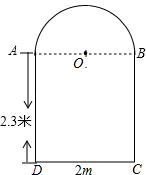
19. 小王与小林进行遥控赛车游戏，终点为点A，小王的赛车从点C出发，以 米/秒的速度由西向东行驶，同时小林的赛车从点B出发，以 米/秒的速度由南向北行驶（如图）.已知赛车之间的距离小于或等于 米时，遥控信号会产生相互干扰， 米， 米，
(1)、出发 秒钟时，遥控信号是否会产生相互干扰？(2)、当两赛车距A点的距离之和为 米时，遥控信号是否会产生相互干扰？20. 综合实践【问题情境】某消防队在一次应急演练中，消防员架起一架长25m的云梯AB，如图，云梯斜靠在一面墙上，这时云梯底端距墙脚的距离.
(1)、【独立思考】这架云梯顶端距地面的距离AC有多高？(2)、【深入探究】消防员接到命令，按要求将云梯从顶端A下滑到位置上（云梯长度不改变）， ， 那么梯子的底端下滑的距离是多少米？(3)、【问题解决】在演练中，高24m的墙头有求救声，消防员需调整云梯去救援被困人员.经验表明，云梯篚墙抾放时，如果云梯底端离墙的距离不小于云梯长度的 ， 则云梯和消防员相对安全.在相对安全的前提下，云梯的顶端能否到达24m高的墙头去救报被困人员？