【基础版】北师大版数学八上 1.3勾股定理的应用 同步练习
试卷更新日期：2024-07-10 类型：同步测试
一、选择题
-
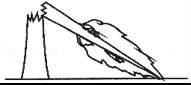
1. 梯子的底端离建筑物6米，10米长的梯子可以到达建筑物的高度是（ ）A、6米 B、7米 C、8米 D、9米2. 如图，一场大风后，一棵大树在高于地面 1 米处折断，大树顶部落在距离大树底部 3 米处的地面上，那么树高是（ ）
A、4m B、 m C、（ +1）m D、（ +3）m3. 如图，有两棵树，一棵高19米，另一棵高10米，两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行（ ）
A、10米 B、15米 C、16米 D、20米4. 如图，斜坡BC的长度为4米．为了安全，决定降低坡度，将点C沿水平距离向外移动4米到点A，使得斜坡AB的长度为4米，则原来斜坡的水平距离CD的长度是（ ）米．
A、2 B、4 C、2 D、65. 如图，为了求出湖两岸A、B两点之间的距离，观测者从测点A、B分别测得 ，又量得 ， ，则A、B两点之间的距离为（ ）
A、10m B、 C、12m D、13m6. 如图，在三角形纸片ABC中， ， ， 折叠三角形纸片，使点A在BC边上的点E处，则AD是
A、3 B、4 C、 D、7. 如图，△ABC中，∠ACB＝90°，AC＝24，BC＝7，点M， N在AB上，且AM＝AC， BN＝BC，则MN的长为（ ）
A、4 B、5 C、6 D、78. 如图所示的“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．该图由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a ， 较短直角边长为b ． 若ab＝10，大正方形面积为25，则小正方形边长为（ ）
A、 B、2 C、 D、3二、填空题
-
9. 如图，是一个三级台阶，它的每一级的长、宽，高分别为 ， 、 ， 和是这个台阶两个相对的端点，点有一只蚂蚁，想到点去吃可口的食物，则蚂蚁沿着台阶面爬到点的最短路程是。
10. 如图，有两棵树，一棵高12米，另一棵高7米，两树相距12米，一只小鸟从一棵树的树梢飞到另一棵树的树梢 ， 则小鸟至少要飞行米．
11. 《九章算术》是古代东方数学代表作，汇集了我国历代学者的劳动和智慧，被誉为人类科学史上应用数学的“算经之首”．其中记录了这样一个问题，原文：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：今有竹高10尺，末端被折断而抵达地面，离竹根部有3尺，则竹的余高为尺．12. 如图，将两个边长为1的小正方形，沿对角线剪开，重新拼成一个大正方形，则大正方形的边长是.
13. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的边长分别是2，3，1，2，则最大正方形E的面积是.
三、解答题
-
14. 如图是一副秋千架，左图是从正面看，当秋千绳子自然下垂时，踏板离地面0.5m（踏板厚度忽略不计）， 右图是从侧面看，当秋千踏板荡起至点B位置时，点B离地面垂直高度BC为1m，离秋千支柱AD的水平距离BE为1.5m（不考虑支柱的直径）.求秋千支柱AD的高.
15. 如图，滑竿在机械槽内运动，为直角，已知滑竿长米，顶点在上滑动，量得滑竿下端距点的距离为米，当端点向右移动米时，滑竿顶端下滑多少米．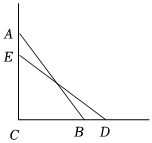
16. “儿童散学归来早，忙趁东风放纸鸢”又到了放风筝的最佳时节．某校八年级班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度 ， 他们进行了如下操作：测得水平距离的长为米；根据手中剩余线的长度计算出风筝线的长为米；牵线放风筝的小明的身高为米．
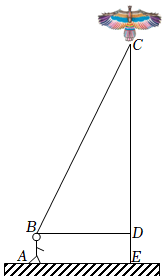(1)、求风筝的垂直高度；(2)、如果小明想风筝沿方向下降米，则他应该往回收线多少米？17. 如图，一辆小汽车在一段限速高速公路上沿直道行驶，某一时刻刚好行驶到路对面车速检测仪的正前方的处，过了后，测得小汽车到达与车速检测仪之间的距离为的处．
(1)、你能计算这辆小汽车的速度吗？(2)、这辆小汽车超速了吗？18. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC为0.7米，梯子顶端到地面的距离AC为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离为1.5米．求小巷的宽．
19. 荡秋千(图1)是中国古代北方少数民族创造的一种运动． 有一天，赵彬在公园里游玩，如图2，他发现秋千静止时，踏板离地的垂直高度 ， 将它往前推送 (水平距离 )时，秋千的踏板离地的垂直高度 ， 秋千的绳索始终拉得很直，求绳索的长度．
20. 如图，在一条绷紧的绳索一端系着一艘小船．河岸上一男子拽着绳子另一端向右走，绳端从C移动到E ， 同时小船从A移动到B ， 绳子始终绷紧且绳长保持不变．
(1)、若CF=7米，AF=24米，AB=18米，求CE的长度．（结果保留根号）(2)、此人以0.5米每秒的速度收绳，请通过计算回答，该男子能否在30秒内将船从A处移动到岸边点F的位置？